
高等数学教案 第三章微分中值定理与导数的应用 第六节函数图形的描绘 教学内容: 在确定了函数的定义域、奇偶性、周期性、单调区间、凹凸区间、极值点、极值、拐点、渐近 线的基础上描绘出函数曲线。 教学目标: 在确定了函数的定义域、奇偶性、周期性、单调区间、凹凸区间、极值点、极值、拐点、渐近 线的基础上描绘出函数曲线。 教学重点: 在确定了函数的定义域、奇偶性、周期性、单调区间、凹凸区间、极值点、极值、拐点、渐近 线的基础上描绘出函数曲线。 教学难点: 在确定了函数的定义域、奇偶性、周期性、单调区间、凹凸区间、极值点、极值、拐点、渐近 线的基础上描绘出函数曲线。教学方法:启发式教学法 作 业:R691,2. 教学过程: 描绘函数图形的一般步骤: (1)确定函数的定义域,并求函数的一阶和二阶导数; (2)求出一阶、二阶导数为零的点,求出一阶、二阶导数不存在的点; (3)列表分析,确定曲线的单调性和凹凸性; (4)确定曲线的渐近性; (⑤)确定并描出曲线上极值对应的点、拐点、与坐标轴的交点、其它点; (6)联结这些点画出函数的图形 例1.画出函数y=x3-x2-x+1的图形 解:(1)函数的定义域为(-0,+o), (2)f'(x)=3x2-2x-1=(3x+1)0x-1),f"(x)=6r-2=2(3x-1). f'x)=0的根为x=-1/3,1;f"(x)=0的根为x=1/3. (3)列表分析:
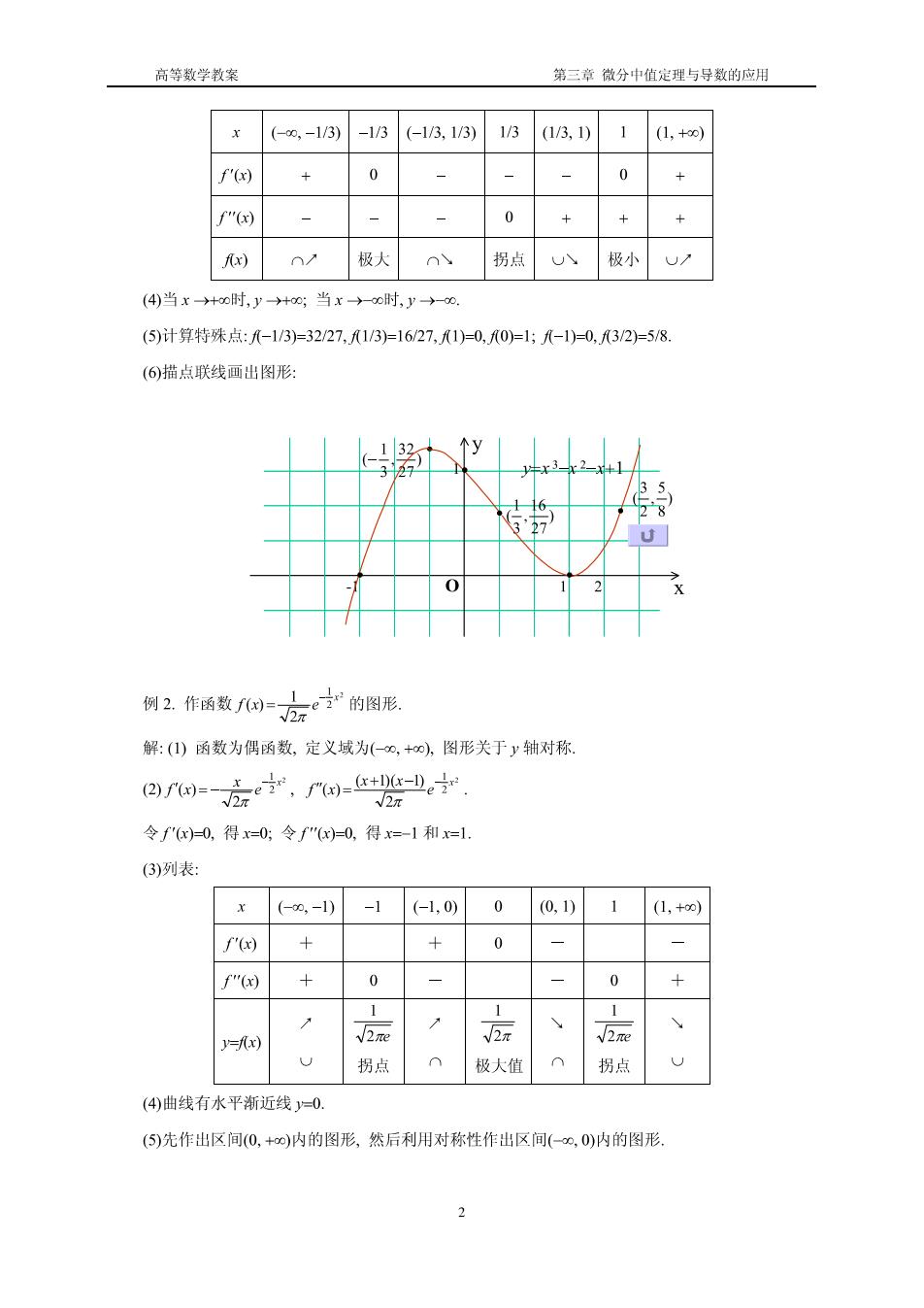
高等数学教案 第三章微分中值定理与导数的应用 (-0,-1/3) -1/3 (-1/3,1/3) 1/3 (1/3,1) (1,+0) f'(x) 0 0 f"(x) 0 + + Rx) 0 极大 n 拐点 U 极小 (4)当x+o时,y+o0;当x→-o时,y→-0. (5)计算特殊点:-1/3)=32/27,1/3)=16/27,1)=0,0)=1;-1)=0,3/2)=5/8. (6)描点联线画出图形: 生x32-+1 例2作函数f国=方云e”的图形 解:(1)函数为偶函数,定义域为(-0,+0),图形关于y轴对称. ②6=方宁产,f--De寸 2π 令f"(x)=0,得x=0;令f"(x)=0,得=-1和x=1. (3)列表: (-0,-1) -1 (-1,0) (0,1) 1 (1,+00) f'(x) + + 0 f"() + 0 0 1 1 y=fx) √2e √2元 √2形 U 拐点 极大值 拐点 (4)曲线有水平渐近线y0. (5)先作出区间(0,+∞)内的图形,然后利用对称性作出区间(-0,0)内的图形, 2

高等数学教案 第三章微分中值定理与导数的应用 例3.作函数y=1+36x (x+3)2 的图形 解:(1)函数的定义域为(-,-3(-3,+). +,/=72-国 (2)f)=363- (x+3)4 令f'(x)=0得x=3,令f"()=0得x=6. (3)列表分析: x (-60,-3) (-3,3) 3 (3,6) 6 (6,+∞) f'(x) + 0 f"(x) 0 + fx) 4极大 11/3拐点 ¥U (4)x=-3是曲线的铅直渐近线,y=1是曲线的水平渐近线, (5)计算特殊点的函数值:0)=1,-1)=-8,-9)=-8,-15)=-11/4 (6)作图. 3