
第二章导数与微分 第一节 导数概念① 基本概念 对于函数y=f(x),研究变量y相对于变量x的变化快慢 即函数变量y对于自变量x的变化率. 1.导数的定义④ 设函数f(x)在x的某邻域内有定义,如果极限 lim Af (xo)_ im fx,+△)-fx)=A存在Q △x-→0 △x △x→0 △x 那么A称为函数f()在点x,的导数, 并称函数y=f(x)在点xo处可导
一、 基本概念 第二章 导数与微分 第一节 导数概念 对于函数 y = f ( x) ,研究变量 y相对于变 量x的变化快慢 即函数变量 y对于自变量x的变化率. 1.导数的定义 A x f x x f x x f x x x = + − = → → ( ) ( ) lim ( ) lim 0 0 0 0 0 存在 如果极限 那 么 A 称 为函 数 f ( x)在 点 0 x 的导数, ( ) , 并称函数y = f x 在 点 x0处可导 设函数 f ( x)在 0 x 的某邻域内有定义
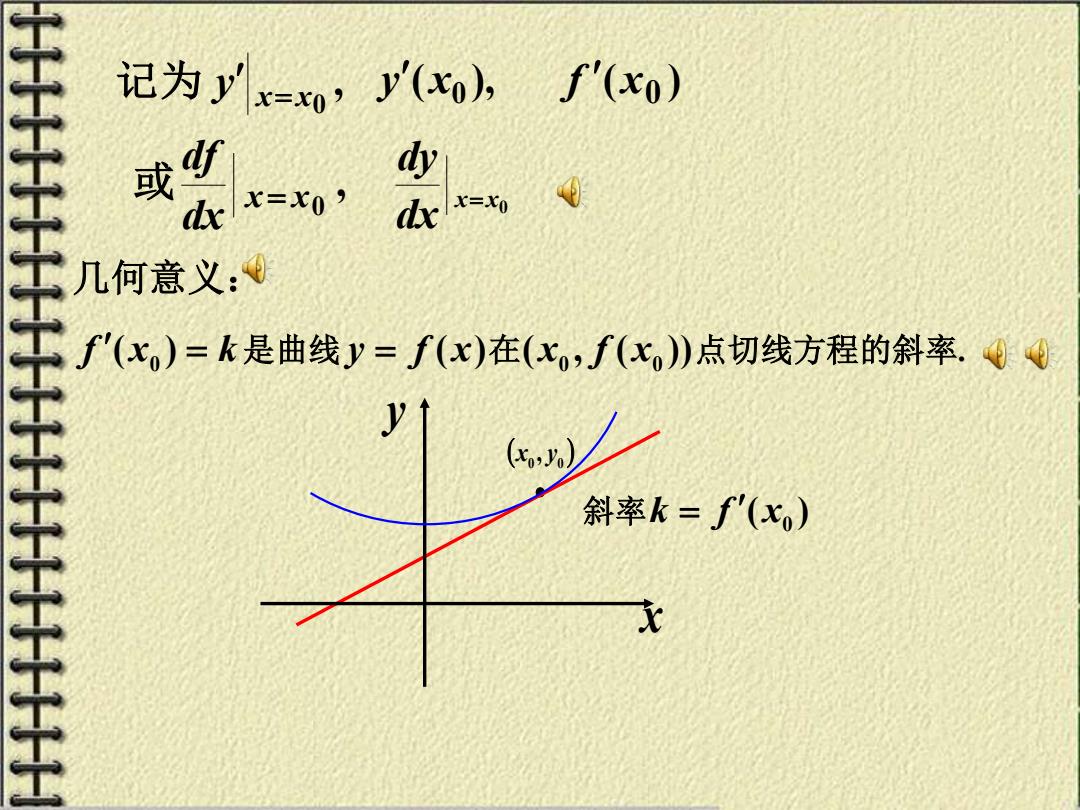
记为yx=o,(x0 f'(xo) x=x0) d欣= 0 几何意义: f'(x)=k是曲线y=f(x)在(x,f(x)点切线方程的斜率.Q t 斜率k=f'(x) 大
, x x0 y = 记为 , 0 x x dx df 或 = ( ) 0 ( ), f x 0 y x x x0 dx dy = 几何意义: f ( x ) = k 0 是曲线 y = f ( x)在( , ( )) 0 0 x f x 点切线方程的斜 率. ( ) • 0 0 x , y x y 斜率 ( ) 0 k = f x

2.单侧导数 1.左导数:0 f(xo)=lim f(x)-fx0)= lim f(xo+Ax)-f(xo) x→x0 x-x0 c→0 c 2.右导数:0 (xo)=Jim手 f(x)-f(o)limf)fo) x→x0 x-x0 年→0+ c 如果函数y=f(x)在区间I上的每点处都可导 就称函数f(x)在区间I上可导f'(x)称为f(x)的④ 导函数(若是含端点的区间,则端点处是单侧导数)
2.右导数: 1.左导数: ; ( ) ( ) lim ( ) ( ) ( ) lim 0 0 0 0 0 0 0 x f x x f x x x f x f x f x x x x + − = − − = → − → − − ; ( ) ( ) lim ( ) ( ) ( ) lim 0 0 0 0 0 0 0 x f x x f x x x f x f x f x x x x + − = − − = → + → + + 2.单侧导数 如果函数y = f (x)在区间I 上的每点处都可导, 就称函数 f (x)在区间I 上可导. f (x)称为f (x) 的 导函数. (若是含端点的区间,则端点处是单侧导数)
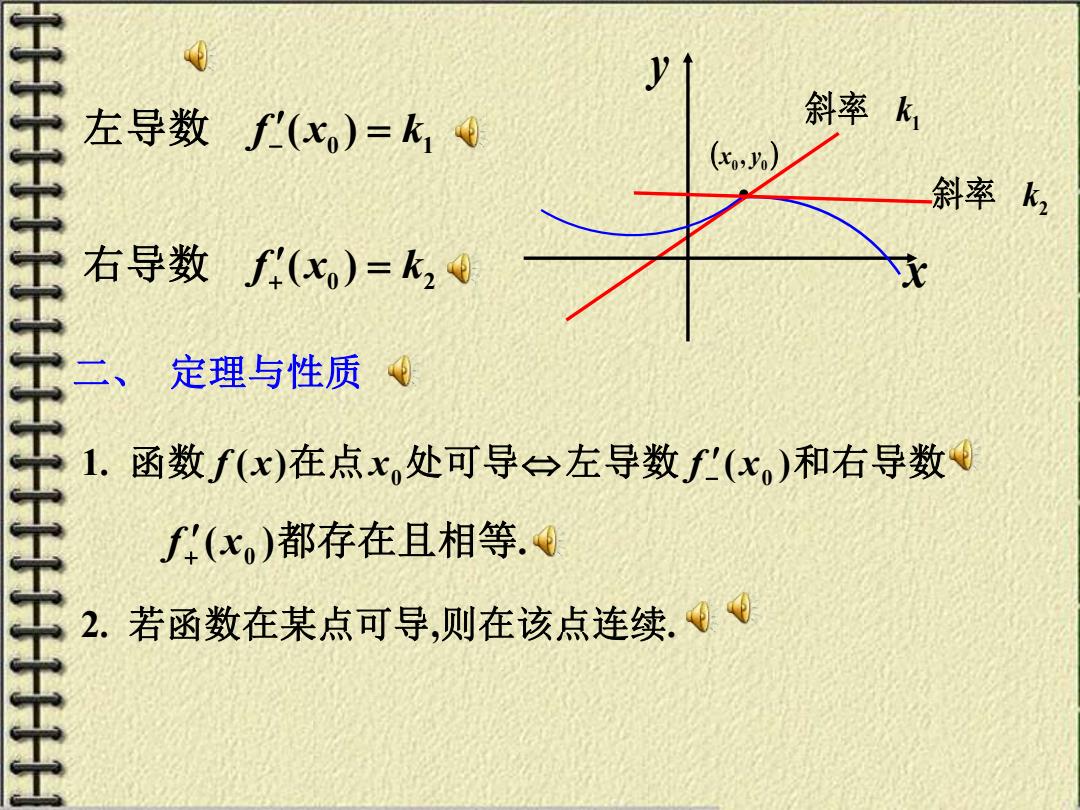
y 左导数f'(x。)=k1 斜率k 斜率k2 右导数f(x)=k2Q 二、 定理与性质 1.函数f(x)在点x处可导台左导数f'(x)和右导数 f(x)都存在且相等.④ 2. 若函数在某点可导,则在该点连续.(
( ) • 0 0 x , y x y 0 1 左导数 f− (x ) = k 0 2 右导数 f+ (x ) = k 1 斜率 k 2 斜率 k 二、 定理与性质 1. 函数 f ( x)在点 0 x 处可导左导数 ( ) 0 f x − 和右导数 ( ) 0 f x + 都存在且相等. 2. 若函数在某点可导,则在该点连续

应用:心 餐置函数d令 (2)v(t)是直线运动的速度函数,则v'(t)=(t)是t时刻的加速度 3).f'(x)=k是曲线y=f(x)在(x,f(x,)点切线方程的斜率④ 常数与基本初等函数的导数④ 例如,求lnx的导数④ (Inx)=lim f(x+△x)-f(x) △x-→0 △x In(1+ lim ln(x+△x)-lnx lim △x→0 △x △x→0 △x
3.应用: (1).s(t)是直线运动的位置函数,则 ( ) ( ) 0 0 s t = v t 是 0 t 时刻的速度. (2).v(t)是直线运动的速 度函数,则 ( ) ( ) 0 0 v t = a t 是 0 t 时刻的加速度. (3). f ( x ) = k 0 是曲 线 y = f ( x)在( , ( )) 0 0 x f x 点切线方程的斜率. 4.常数与基本初等函数的导数 例如,求ln x的导数 x f x x f x x x + − = → ( ) ( ) (ln ) lim 0 x x x x x x x x x + = + − = → → ln(1 ) lim ln( ) ln lim 0 0

ln(1+ Ar) 利用等价代换 lim lim △x→0 △x △x-→0 HIx 得到导数公式 (lnx)= 些基本的导数公式④ 1.(C)'=0 2.(x“y=x4.(u∈R) 3.(sinx)'=cosx. 4. (cosx)=-sinx 5. (a)-axIna. 特别: (ex)'=ex. 6. (og=1log。e. 特别:山y-士心
利用等价代换 x x x x x x x x x 1 lim ln(1 ) lim 0 0 = = + → → 得到导数公式 x x 1 (ln ) = 一些基本的导数公式 1. (C) = 0 3. (sin x) = cos x. 2. ( ) . ( ) 1 x = x R − 4. (cos x) = −sin x 5. (a ) a lna. x x = : ( ) . x x 特别 e = e log . 1 6. (log ) e x x a = a . 1 : (ln ) x 特别 x =

三、课前思考问题④ 利用定义计算函数:C,x“,sinx,cosx,log。x 的导数 说明函数在某点可导必然在该点连续,并举例说明反之不成立, 3.说明函数在某点可导的充分必要条件是函数在该点左右导数存在 并且相等
三、 课前思考问题 1. 利用定义计算函数:C , x ,sin x,cos x,loga x 的导数. 2. 说明函数在某点可导必然在该点连续,并举例说明反之不成立. 3. 说明函数在某点可导的充分必要条件是函数在该点左右导数存在 并且相等