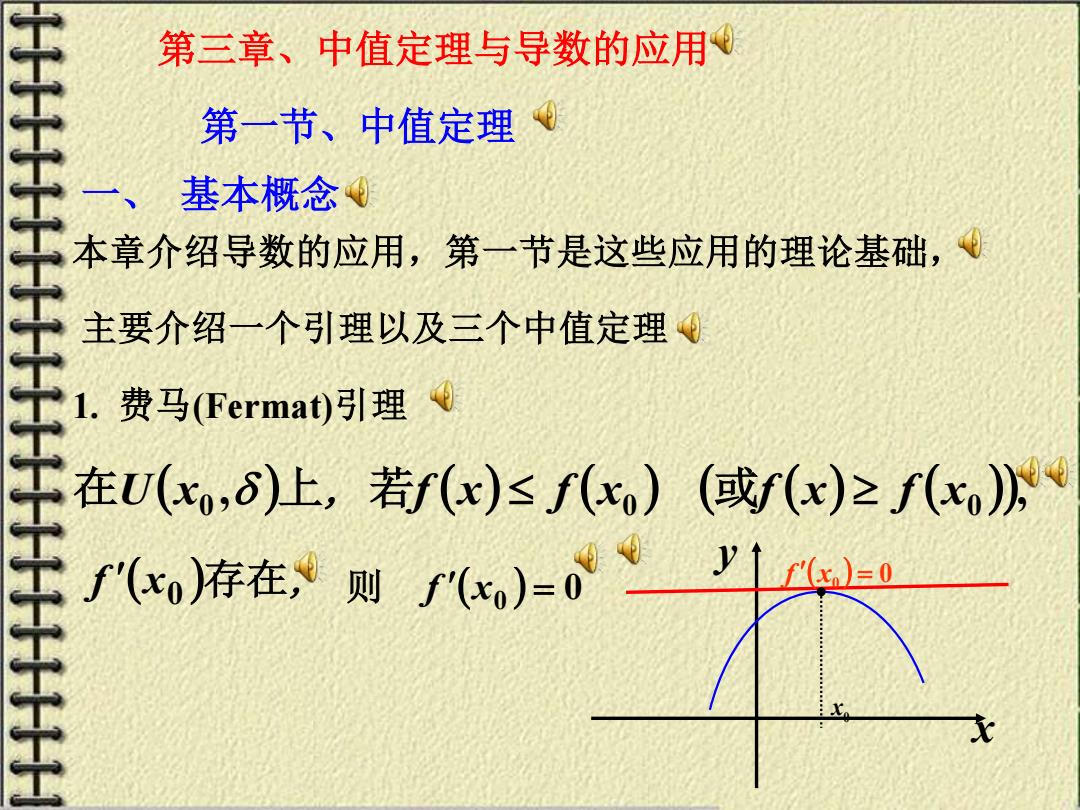
第三章、中值定理与导数的应用 第一节、中值定理 一、基本概念 本章介绍导数的应用,第一节是这些应用的理论基础, 主要介绍一个引理以及三个中值定理④ 1. 费马(Fermat)引理 在U(xo,6)上,若f(x)f(x)(或f(x)≥f(x) f(x)存在,9则f)=0'10
一、 基本概念 第三章、中值定理与导数的应用 本章介绍导数的应用,第一节是这些应用的理论基础, 第一节、中值定理 主要介绍一个引理以及三个中值定理 1. 费马(Fermat)引理 f (x0 )存在, ( , ) ( ) ( ) ( ( ) ( )), 0 0 x0 在U x 上, 若f x f x 或f x f 则 f (x0 ) = 0 x y 0 x ( ) 0 f x0 =

2、 罗尔(Rolle)定理g函数f(x)(1)闭区间[a,b1上连续,Q (2)在开区间(a,b)内可导, (3)区间端点的函数值相等,即f(a)=f(b), 那末在(a,b)内至少有一点(M<飞<b),0 干王王王王王 使得函数f(x)在该点的导数等于零,即f'(5)=0 例如f(x)=(x-1)(x-2)20 y=f(x) (1,2)内至少有一点50 0 使得f'(5)=0.0 51 2 b x
2、罗尔(Rolle)定理 (2)在开区间(a,b)内可导, (3)区间端点的函数值相等,即 f (a) = f (b), 那末在(a, b)内至少有一点(a b), 使得函数 f ( x)在该点的导数等于零, 即 f ( ) = 0 函数 f ( x)(1)闭区间 [a,b]上连续, a 1 2 b x y o y = f (x) C 例如 2 f ( x) = ( x − 1)( x − 2) 在 (1,2)内至少有一点 使得 f ( ) = 0
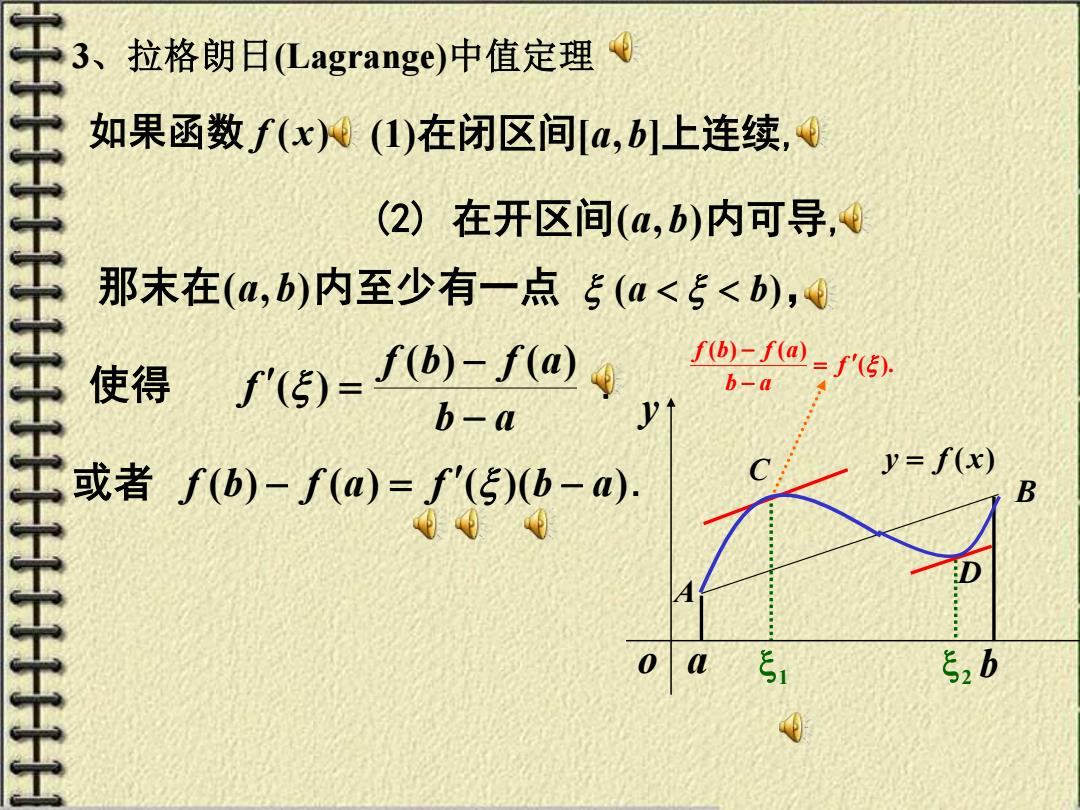
3、 拉格朗日(Lagrange)中值定理《 如果函数f(x)(1)在闭区间[a,b上连续, (2)在开区间(a,b)内可导,0 那末在(a,b)内至少有一点5(a<5<b),④ 使得 f'(5)= fb)-f(四g fb)-f@=f'传) b-a b-a 或者f(b)-f()=f'(5)b-a). y=f(x) 日00 52b
3、拉格朗日(Lagrange)中值定理 如果函数 f ( x) (2) 在开区间(a,b)内可导, 那末在(a, b)内至少有一点 (a b), 或者 f (b) − f (a) = f ( )(b − a). (1)在闭区间[a,b]上连续, 使得 b a f b f a f − − = ( ) ( ) ( ) . o a 1 2 b y y = f (x) A B C D ( ). ( ) ( ) f b a f b f a = − −

应用:0f(x)是区间1上的可导函数,9 (1)如果f'(x)>0,则f(x)是I上的单调递增函数. (2)如果f'(x)<0,则f(x)是I上的单调递减函数.④④④ 柯西(Cauchy)中值定理Q 如果函数f(x)及g(x)在闭区间[a,b]上连续,① 在开区间(a,b)内可导,且g'(x)在(a,b)内每一点处均不为零, 那末在(a,b)内至少有一点(a<<b),④ 使等式 f(b)-f(四)_f'(5) 成立. 3(b)-3(a) g'(5)
应用: (1)如果 f ( x) 0,则 f ( x)是I上 的单调递增函数. 4、柯西(Cauchy)中值定理 如果函数 f ( x)及g( x)在闭区间[a, b]上连续, 在开区间(a,b)内可导,且g ( x)在(a, b)内每一点处均不为零, 那末在(a,b)内至少有一点(a b), 使等式 ( ) ( ) ( ) ( ) ( ) ( ) g f g b g a f b f a = − − 成立. (2)如 果 f ( x) 0,则 f ( x)是I上 的单调递减函数. f ( x)是区间I 上的可导函数

三、课前思考问题 1.证明:在区间I上f'(x)>0,fx)是单调递增函数.④ 2.f(x)是二阶可导函数,如果f(a)=f(c)=f(b).0 证明:存在5∈(a,b)使得f"(5)=0,其中a<c<b. f(x),g(x)是可导函数,f(0)=g(0)=0,g'(x)≠0.④ 则只要x≠0,必存在0<0<1,使得 f(x)f() g(x)g'()
三、 课前思考问题 1. 证明:在区间I 上 f ( x) 0, f ( x)是单调递增函数. 2. f ( x)是二阶可导函数,如果 f (a) = f (c) = f (b). 证明:存在 (a,b)使得 f ( ) = 0, 其中a c b. 3. f ( x),g( x)是可导函数, f (0) = g(0) = 0,g ( x) 0. 则只要x 0,必存在0 1, 使得 ( ) ( ) ( ) ( ) g x f x g x f x =