
第四节 函数的单调性与曲线的凹凸性 一、 基本概念④ 如果在区间I上任意两点x1f(x2) 则称f(x)是区间I上的单调递增函数(或者单调递增函数) 函数的单调性(单调递增、单调递减)
一、 基本概念 第四节 函数的单调性与曲线的凹凸性 1. 如果在区间I 上任意两点 1 2 x x 都有 ( ) ( ) 1 2 f x f x , 则称 f ( x)是区间I上的单调递增函数(或者单调递增函数) (或者 ( ) ( ) 1 2 f x f x ) 函数的单调性(单调递增、单调递减)

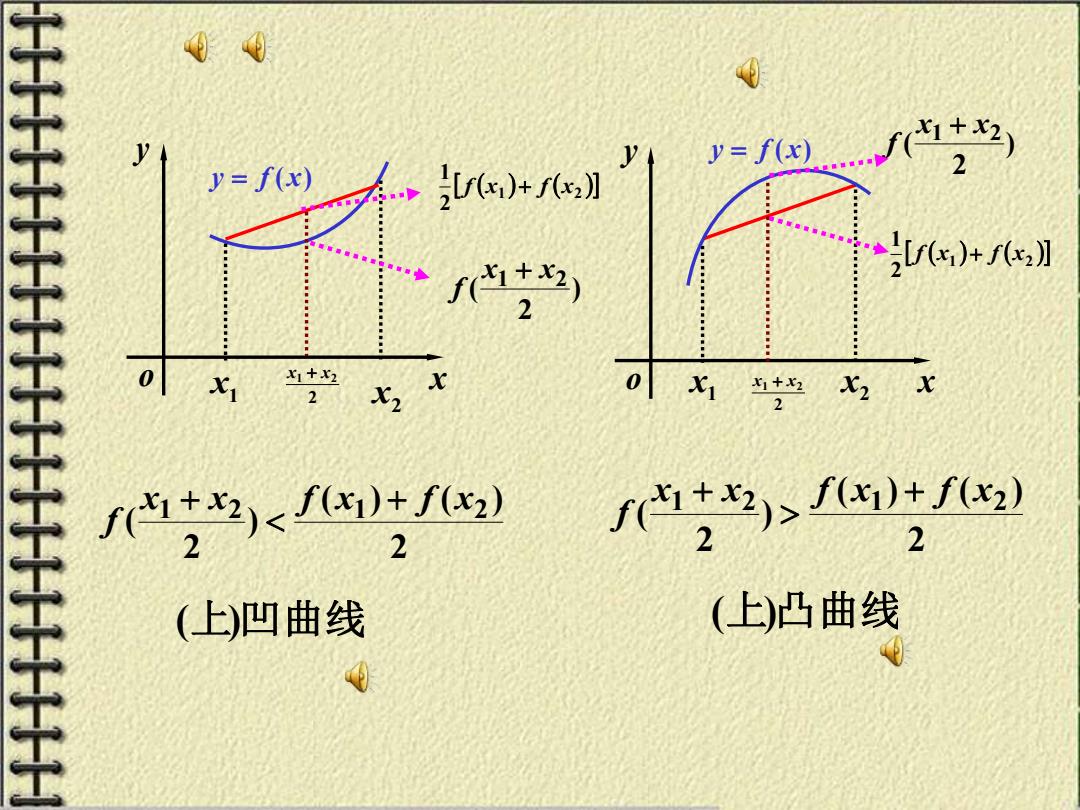
设f(x)是区间I上的连续函数,如果对于I上任意 不何的两点都有/)儿片f 2 那末称f(x)在I上的图形是(向上)凹的;④ 如果对1上任意不同两点x1,x2,恒有 f)>生f. 2 那末称f(x)在I上的图形是(向上)凸的;① 曲线上凹凸的分界点(x,y)称为曲线的拐点Q
如果对I上任意不同两点x1 , x2 , 恒 有 那末称 f (x)在I上的图形是(向 上)凹 的; , 2 ( ) ( ) ) 2 ( 1 2 1 x2 x x f x f f + + 那末称 f (x)在I上的图形是(向 上)凸 的; 2. 设 f ( x)是区间I 上的连续函数, 不同的两点 1 2 x , x 都 有 2 ( ) ( ) ) 2 ( 1 2 1 2 x x f x f x f + + 曲线上凹凸的分界点( , ) 0 0 x y 称为曲线的拐点 如果对于I 上任意
y y=f(x) =四) t o 0 七xx < 2 ) 2 (上)凹曲线 (上)凸曲线
x y o y = f ( x) x1 x2 2 1 2 x + x x y o 1 x 2 x y = f ( x) ) 2 ( x1 x2 f + ( ) ( ) 1 2 2 1 f x + f x ( ) ( ) 1 2 2 1 f x + f x ) 2 ( x1 x2 f + 2 x1 + x2 2 ( ) ( ) ) 2 ( 1 2 1 x2 x x f x f f + + 2 ( ) ( ) ) 2 ( 1 2 1 2 x x f x f x f + + (上)凹曲线 (上)凸曲线

定理与性质④ 设函数y=f(x)在a,b]上连续在(a,b)内可导d (1)如果在a,b)内f'(x)>0, 那末函数y=f(x)W 在[,b]上单调增加0(2)如果在(a,b)内f'(x)<0, 那末函数y=f(x)在[a,b]上单调减少d
二、 定理与性质 那末函数y = f (x)在[a,b]上单调减少. (1) 如果在(a,b)内f (x) 0, 1. 设函数y = f (x)在[a,b]上连续,在(a,b)内可导. 在[a,b]上单调增加; (2)如果在(a,b)内f (x) 0, 那末函数y = f (x)
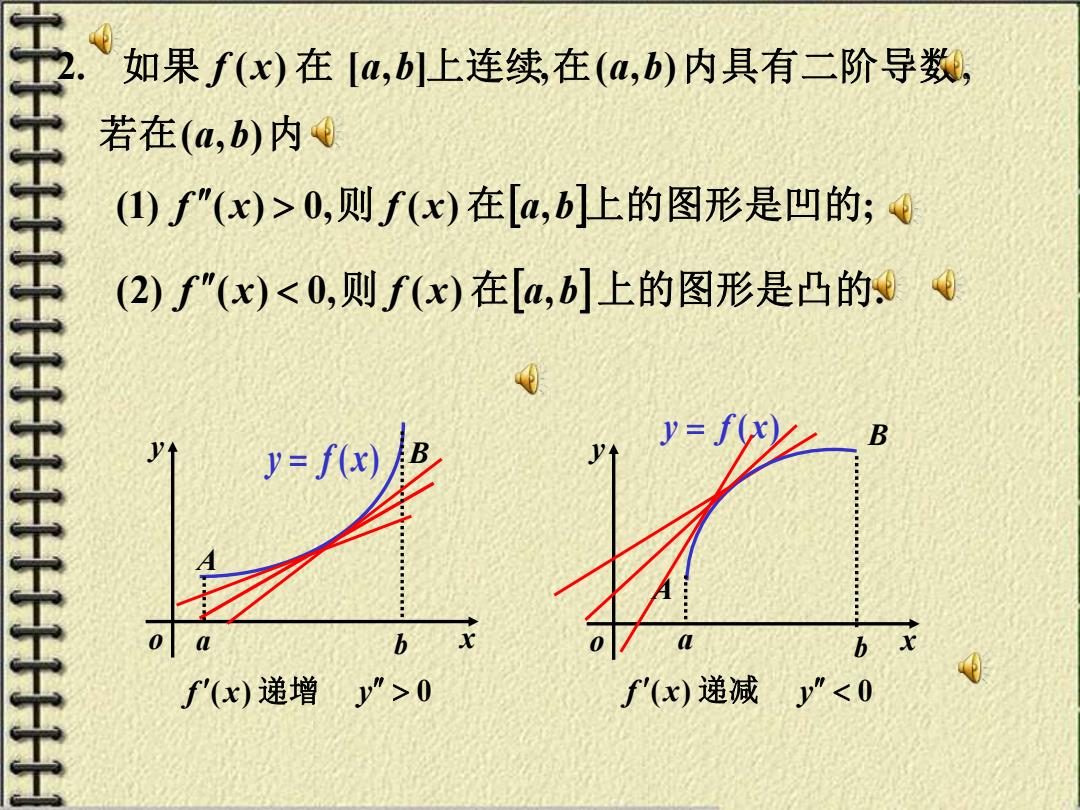
如果f(x)在[a,b]上连续,在(a,b)内具有二阶导数, 若在(a,b)内d (I)"(x)>0,则f(x)在[a,b]上的图形是凹的;d (2)f"(x)0 f'(x)递减y"<0
x y o y = f (x) x y o y = f (x) a b A B f (x) 递增 a b B A y 0 f ( x) 递减 y 0 2. 如 果 f ( x) 在 [a,b]上连续,在(a,b)内具有二阶导数, 若在(a,b)内 (1) f (x) 0,则 f (x) 在a,b上的图形是凹的; (2) f (x) 0,则 f (x) 在a,b上的图形是凸的

例.讨论y=xe的单调性与凹凸性.Q y'=(x+1)e*0 函数y=xe在x≤-1上单调递减 在x≥-1上单调递增④ y"=(x+2)e'④ 在x≤-2上,y=xe是(上)凸曲线④ 在x≥-2上,y=xe是(上)凹曲线. (-2,-2e-2)是曲线的拐点.0
例. 讨论 x y = xe 的单调性与凹凸性. x y = (x + 1)e x y = (x + 2)e 函数 x y = xe 在 x −1上单调递减 在 x −2上, x y = xe 是(上)凸曲线 在 x −1上单调递增 在 x −2上, x y = xe 是(上)凹曲线. ( 2, 2 ) −2 − − e 是曲线的拐点

三、课前思考问题 1.利用中值定理证明:在区间上f'(x)>0函数单调递增.《 2.证明在区间a,b]上,f"(x)>0,则f(x)的图形是凹的 3.( 1)利用函数的单调性证明:a>b(b>a>e) (2)利用曲线的凹凸性证明不等式: ana+bnb>(a+6n()( b>a>0)
三、 课前思考问题 1.利用中值定理证明:在区间上 f ( x) 0 函数单调递增. 2. 证明在区间[a,b]上 ,f (x) 0,则 f (x)的图形是凹的 (2)利用曲线的凹凸性证明不等式: ) ( 0) 2 ln ln ( )ln( + + + b a a b a a b b a b 3.(1)利用函数的单调性证明:a b (b a e) b a