
第五节 函数的极值与最大最小值④ 工二二二主二二二二主二二二十土 一、基本概念 1. 极值:如果存在一个x,的领域U(x。),使得 f(x)f(x))当≠x,时成立, 就称f(x)是函数f(x)的一个极大值(或极小值)① x称为f(x)的极值点.① 极大值 N 极小值 xo 0 xo
一、 基本概念 第五节 函数的极值与最大最小值 1. 极值: 如果存在一个 0 x 的领域 ( ) 0 U x ,使得 ( ) ( ) ( ( ) ( ) ) 0 0 f x f x 或f x f x 当 0 x x 时成立, 就 称 ( ) 0 f x 是函数 f ( x)的一个极大值(或极小值) 极大值 o x y o x y x0 0 x 极小值 0 x 称为 f ( x)的极值点

2.最大、最小值 函数f(x)在区间I上有定义,如果有x。∈I,使得① f(x)≤f(x)(或f(x)≥f(x)在区间I上恒成立,《 则称f(x)是f(x)在I上的最大值(或最小值 x,称为f(x)在I上的最大值点(或最小值点)① 例如f(x)=x,0≤x<1有最小值f(0)=0,没有最大值.00
2.最大、最小值 函 数 f ( x)在区间I 上有定义,如果有x I 0 ,使 得 则称 ( ) 0 f x 是 f ( x)在I 上的最大值(或最小值) ( ) ( ) 0 f x f x (或 ( ) ( ) 0 f x f x )在区间I 上恒成立, 0 x 称为 f ( x)在I 上的最大值点(或最小值点) 例 如 f ( x) = x, 0 x 1有最小值 f (0) = 0,没有最大值

工王 定理与性质④ (必要条件如果x。是f(x)的极值点,f(x)在x,点可导, 则f'(x)=C0(若f'(x)=0称x是f(x)的驻点) 注:若x,是f(x)在区间I的最(大,小)值点,并且x。Q 不是区间I的端点,若如果f'()存在,必有f'(x)=0 (第一充分条件)④ 如果f(x)在U(xo,δ)上连续, 0 在U(x,δ)上可导0 x是f(x)的极值点,则④ (1)当x∈(x,-6,xo),有f'(x)>0;而x∈(x,x0+6),0 有f'(x)<0,则f(x)在x处取得极大值0d
二、 定理与性质 1. (必要条件) (若 f ( x0 ) = 0 称x0是 f ( x)的驻点) 注:若 0 x 是 f ( x)在区间I的最(大,小)值点,并且 0 x 不是区间I的端点,若如果 ( ) 0 f x 存在,必有 ( ) 0 f x0 = 2. (第一充分条件) 则 ( ) 0 f x0 = 0 x 是 f ( x)的极值点,则 有 f ( x) 0,则 f ( x)在 0 x 处取得极大值. (1)当 ( , ), 0 0 x x − x 有 f ( x) 0;而 ( , ) x x0 x0 + , 如果 0 x 是 f ( x)的极值点, f (x)在 0 x 点可导, 如果 f ( x)在 ( , ) U x0 上连续, 在 ( , ) 0 0 U x 上可导
(2)如果x∈(x-6,x),有f'(x)0,则f(x)在x,处取得极小值. (3)如果当x∈(x-6,x)及x∈(x,x,+6)时,0 f'(x)符号相同,则f(x)在x,处无极值.Q ④y (是极值点情形) Xo x 0 Xo X y 不是极值点情形) 0 Xo x 0 Xo
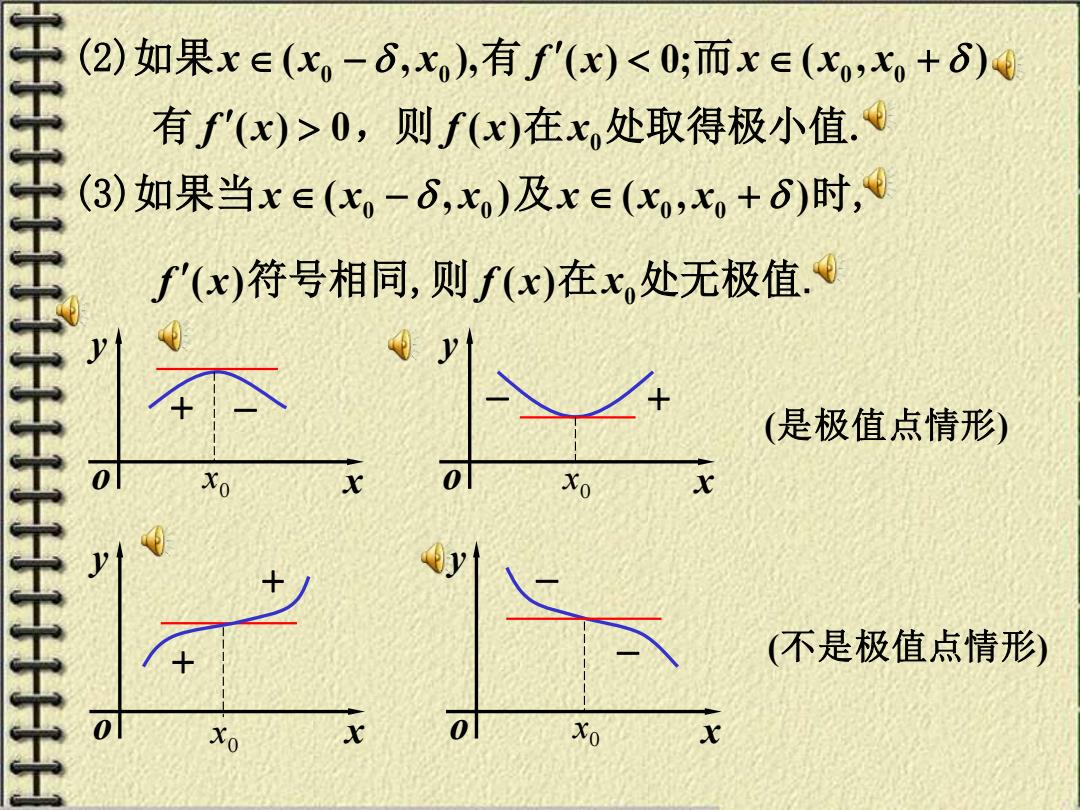
(3)如果当 ( , ) 0 0 x x − x 及 ( , ) x x0 x0 + 时, (2)如果 ( , ), 0 0 x x − x 有 f ( x) 0;而 ( , ) x x0 x0 + 有 f ( x) 0,则 f ( x)在 0 x 处取得极小值. f ( x)符号相同,则 f ( x)在 0 x 处无极值. x y o x y x0 o 0 x + − − + (是极值点情形) x y o x y o 0 x 0 x + − − + (不是极值点情形)

3 (第二充分条件)设f(x)在x处具有二阶导数, 且f'(x)=0,f"(x)≠0,那么《 (1)当f"()0时,函数f(x)在x处取得极小值. (最大,最小值)设f(x)是区间I上的可导函数, 若f(x)是函数f(x)在I上的最大或最小值,则⑤ x是f(x)驻点或者是区间I的端点.④④④
且 f ( x0 ) = 0, f ( x0 ) 0,那么 (1)当 f ( x0 ) 0时, 函数 f ( x)在 x0处取得极大值; (2)当 ( ) 0 f x0 时, 函数 f ( x)在 0 x 处取得极小值. 3. (第二充分条件) 4. (最大,最小值) 若 ( ) 0 f x 是函 数 f ( x)在I上 的最大或最小值,则 0 x 是 f ( x)驻点或者是区间I的端点. 设 f ( x)在 0 x 处具有二阶导数, 设 f ( x)是区间I上的可导函数

讨论函数y=2x3+3x2-12x+14抽-3,4]Q 上的极值与最大最小值④ ·f'(x)=6(x+2)x-1)0解方程f'(x)=0,得驻点 6--2,52=1.990 f"(x)=12x+60 f"(-2)=-1800 f(1)=7是极小值0 比较f(-2)=34;f1)=7;4f(-3)=23;f(4)=142 得到最大值f(4)=14经, 最小值f(1)=7
f (x) = 6(x + 2)(x −1) 2 3 12 14 [ 3,4] 3 2 例如 讨论函数 y = x + x − x + 在 − 解方程 f (x) = 0,得驻点 2, 1. x1 = − x2 = 比较 f (−2) = 34; f (1) = 7; f (−3) = 23; f (4) = 142 上的极值与最大最小值 f (x) = 12x + 6 f (−2) = −18 0 f (−2) = 34 是极大值 f (1) = 18 0 f (1) = 7 是极小值 得到最大值 f (4) = 142, 最小值 f (1) = 7

三、课前思考问题④ 可导函数的极值点一定是它的驻点, 举例说明:驻点未必是可导函数的极值点.④ 2. 说明第一充分条件的几何意义. 3.若f(x)是极小值,是否函数f(x)在x,的某邻域内Q 左侧下降,右侧上升.分析函数④ 2+r2+sin x≠0 f(x)= 2, x=0
三、 课前思考问题 1 .可导函数的极值点一定是它的驻点, 举例说明:驻点未必是可导函数的极值点. 2.说明第一充分条件的几何意义. = + + = 2, 0 ), 0 1 2 (2 sin ( ) 2 x x x x f x . 3 .若 ( ) x0 f 是极小值,是否函数 f (x)在x0的某邻域内 左侧下降,右侧上升.分析函数