
第三节泰勒(Taylor)公式 一、基本概念 工二二主二二二二二二二十土 如果函数f(x)可导,则f(x)-f(x)=f'(5)(x-x)W 或f(x)=f(x)+f'(5)(x-x)称为拉格朗日中值定理. 如果函数f(x)具有可导n或n+1阶导数本节介绍一个④ 更一般的中值定理:泰勒中值定理,又称为泰勒公式《
一、 基本概念 第三节 泰勒(Taylor)公式 如果函数 f ( x)可导,则 ( ) ( ) ( )( ) 0 0 f x − f x = f x − x 或 ( ) ( ) ( )( ) 0 0 f x = f x + f x − x 称为拉格朗日中值定理. 如果函数 f ( x)具有可导 n或n + 1 阶导数, 更一般的中值定理:泰勒中值定理,又称为泰勒公式 本节介绍一个

定理与性质 1.泰勒公式0 如果函数f(x)在含有x,的某个开区间(a,b)内具有直到 (n+1)阶的导数则当x在(a,b)内时, f()=f()+fo)x-x0)-xo) 21 ++fm(x-0+R(四0 n! 其中R(心=f5x-x,(5在x与x之间。 (n+1): 注:5又可记为x0+(x-x)其中0<0<1400
其中 1 0 ( 1) ( ) ( 1)! ( ) ( ) + + − + = n n n x x n f R x ( 在x0与x之间). 如果函数 f ( x)在含有 0 x 的某个开区间(a,b)内具有直到 (n + 1)阶的导数, 则当x在(a,b)内时, 2 0 0 0 0 0 ( ) 2! ( ) ( ) ( ) ( )( ) x x f x f x f x f x x x − = + − + ( ) ( ) ! ( ) 0 0 ( ) x x R x n f x n n n ++ − + ( ) 0 1 注 : 又可记为x0 + x − x0 其 中 二、 定理与性质 1.泰勒公式

R {-广52 称为拉格朗日形式的余项 又小 =:-+4-1+ k! (x-x0)"]。称为佩亚诺形式的余项Q
( ) 0 0 0 0 ( ) ( ) ( ) [( ) ] ! k n k n k f x f x x x o x x = k 又 = − + − [( 0 ) ] 称为佩亚诺形式的余项 n o x − x 称为拉格朗日形式的余项 ( ) + + = − + ( 1) 1 0 ( ) ( ) ( ) 1 ! n n n f R x x x n ,( 0 在x x 与 之间)

麦克劳林公式 fx=f0+f0x+202++f0x" 2! n! +ftax1 (0<0<1)0 (n+1)g =0+ox,,+0x+ 2! n! (带佩亚诺余项的麦克劳林公式)
( ) ! (0) 2! (0) ( ) (0) (0) 0 ( ) 2 n n n x x n f x f f x f f x + + + = + + 2.麦克劳林公式 (带佩亚诺余项的麦克劳林公式) n n x n f x f f x f f x ! (0) 2! (0) ( ) (0) (0) ( ) 2 + + = + + (0 1) ( 1)! ( ) 1 ( 1) + + + + n n x n f x

3. 常用函数带佩亚诺余项的麦克劳林公式 =0to+/0+0+e =1+x+ ++ 2! n! +0(x").0 sinx= + 5 :+o(r2n*)0 COSx 1~ 2: 4! 8*-小8* x ln(1+x)=x- 2 3 +0(x+1)W n+l
3. 常用函数带佩亚诺余项的麦克劳林公式 ( ) (2 1)! ( 1) 3! 5! sin 2 1 3 5 2 1 + + + + = − + − + − n n n o x n x x x x x ( ) (2 )! ( 1) 2! 4! 6! cos 1 2 2 4 6 2 n n n o x n x x x x x = − + − ++ − + ( ) 1 ( 1) 2 3 ln(1 ) 1 2 3 1 + + + + + = − + − + − n n n o x n x x x x x 0( ). 2! ! 1 2 n n x x n x x e = + x + ++ + ( ) ! (0) 2! (0) ( ) (0) (0) 0 ( ) 2 n n n x x n f x f f x f f x + + + = + +
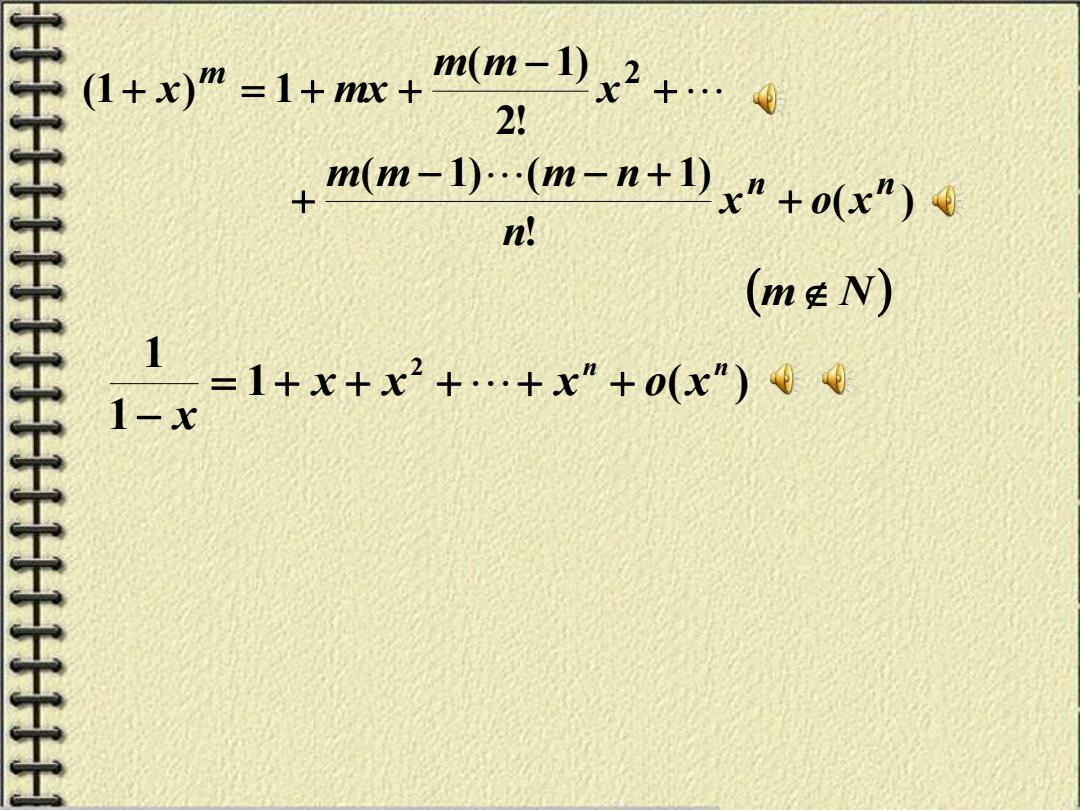
(1+x)m=1+xe m2+4 2! mm-)-m-n+1)x"+o(x") n! (mgN) 1 =1+x+x2+…+x"+0(x")00 1-x
+ − + = + + 2 2! ( 1) (1 ) 1 x m m x mx m ( ) ! ( 1) ( 1) n n x o x n m m m n + − − + + 1 ( ) 1 1 2 n n x x x o x x = + + + + + − (m N)

例如利用泰勒公式求极限im e*sinx-x(1+x) x→0 七3 24 +or sinx=x 3! +0(x3)0 lim e*sinx-x(1+x)_ x→0 (1+x+ +o(x3)-x(1+x) lim 2!3 x-→0 3 2!3! +0(x3) 1 lim x→>0 x3 3
( ), 2! 3! 1 3 2 3 o x x x e x x = + + + + ( ) 3! sin 3 3 o x x x = x − + = − + → 3 0 sin (1 ) lim x e x x x x x 3 3 3 3 2 3 0 ( )) (1 ) 3! ( )) ( 2! 3! (1 lim x o x x x x o x x x x x x + + + + − + − + → 3 1 ( ) 2! 3! lim 3 3 3 3 0 = − + = → x o x x x x 例如利用泰勒公式求极限 3 0 sin (1 ) lim x e x x x x x − + →

课前思考问题④ 1.正确叙述泰勒公式与麦克劳林公式的条件与结论④ 并解释拉格朗日与佩亚诺形式的余项的概念。 2. 利用公式推导出所列出基本函数的麦克劳林公式 3.写出sinx带有佩亚诺形式余项的n阶麦克劳林公式.W
三、 课前思考问题 1. 正确叙述泰勒公式与麦克劳林公式的条件与结论 2. 利用公式推导出所列出基本函数的麦克劳林公式 并解释拉格朗日与佩亚诺形式的余项的概念. 3. 写 出 x 2 sin 带 有佩亚诺形式余 项的n阶麦克劳林公式