
高等数学期末复习 可少习程学院
高等数学期末复习

第一章 函数与极限 (1)理解极限的概念 (2)理解无穷小量,无穷大量的概念,了解无穷小量的运算性质及其 与无穷大量的关系; (3)掌握极限的四则运算法则,掌握两个重要极限,掌握求极限的常 用方法; (④)理解函数在某点连续的概念,知道左连续和右连续的概念,会判 断函数在某点的连续性; (⑤)了解函数间断点的概念,会求函数的间断点,会判别函数间断点 的类型; (6)了解“初等函数在定义区间内连续”的结论,知道闭区间上的连 续函数的几个性质。 学院
第一章 函数与极限 ⑴理解极限的概念 ⑵理解无穷小量,无穷大量的概念,了解无穷小量的运算性质及其 与无穷大量的关系; ⑶掌握极限的四则运算法则,掌握两个重要极限,掌握求极限的常 用方法; ⑷理解函数在某点连续的概念,知道左连续和右连续的概念,会判 断函数在某点的连续性; ⑸了解函数间断点的概念,会求函数的间断点,会判别函数间断点 的类型; ⑹了解“初等函数在定义区间内连续”的结论,知道闭区间上的连 续函数的几个性质

第二章导数与微分 (1)理解导数与微分概念,了解导数的几何意义,会求曲线的切线和 法线方程,知道可导与连续的关系; (2)熟记导数与微分的基本公式,熟练掌握导数与微分的四则运算法 则; (3)掌握复合函数的求导法则; (4)掌握隐函数的求导法则、由参数方程确定的函数的求导法则,对 数求导数的方法; (⑤)知道一阶微分形式的不变性; (6)了解高阶导数概念,掌握求函数的二阶导数的方法,会求高阶导 数
第二章 导数与微分 ⑴理解导数与微分概念,了解导数的几何意义,会求曲线的切线和 法线方程,知道可导与连续的关系; ⑵熟记导数与微分的基本公式,熟练掌握导数与微分的四则运算法 则; ⑶掌握复合函数的求导法则; ⑷掌握隐函数的求导法则、由参数方程确定的函数的求导法则,对 数求导数的方法; ⑸知道一阶微分形式的不变性; ⑹了解高阶导数概念,掌握求函数的二阶导数的方法, 会求高阶导 数

第三章微分中值定理与导数的应用 (1)了解罗尔定理、拉格朗日中值定理何柯西中值的条件和结论,会 用他们证明一些结论; (2)掌握洛比塔法则,能用它求未定式的极限; (3)掌握用一阶导数求函数单调区间、极值与极值点(包括判别)的方 法,了解可导函数极值存在的必要条件,知道极值点与驻点的区别与 联系; (④)掌握用二阶导数求曲线凹凸(包括判别)的方法,会求曲线的拐点: (⑤)会求曲线的水平渐近线和垂直渐近线和斜渐近线: (6)掌握求解一些简单的实际问题中最大值和最小值的方法。 D可程学院
第三章 微分中值定理与导数的应用 ⑴了解罗尔定理、拉格朗日中值定理何柯西中值的条件和结论,会 用他们证明一些结论; ⑵掌握洛比塔法则,能用它求未定式的极限; ⑶掌握用一阶导数求函数单调区间、极值与极值点(包括判别)的方 法,了解可导函数极值存在的必要条件,知道极值点与驻点的区别与 联系; ⑷掌握用二阶导数求曲线凹凸(包括判别)的方法,会求曲线的拐点; ⑸会求曲线的水平渐近线和垂直渐近线和斜渐近线; ⑹掌握求解一些简单的实际问题中最大值和最小值的方法

第四章不定积分 (1)理解原函数与不定积分概念,了解不定积分的性质以及积分 与导数(微分)的关系; (2)掌握积分基本公式和直接积分法; (3)掌握第一换元积分法和分部积分法; (④)掌握第二换元积分法。 D可程学院
第四章 不定积分 ⑴理解原函数与不定积分概念,了解不定积分的性质以及积分 与导数(微分)的关系; ⑵掌握积分基本公式和直接积分法; ⑶掌握第一换元积分法和分部积分法; ⑷掌握第二换元积分法

第五章定积分 (1)理解定积分的概念,了解定积分的性质; (2)掌握积分上限函数,牛顿莱布尼公式; (3)掌握定积分的换元积分法和分部积分法: D可程学院
第五章 定积分 ⑴ 理解定积分的概念,了解定积分的性质; ⑵ 掌握积分上限函数,牛顿莱布尼公式; ⑶ 掌握定积分的换元积分法和分部积分法;

第六章定积分的应用 (1)掌握直角坐标系下平面图形的面积的求法 (2)了解极坐标下平面图形的面积的求法 (3)掌握旋转体体积的求法 (4)会求平面曲线的弧长 D可程学院
第六章 定积分的应用 (1)掌握直角坐标系下平面图形的面积的求法 (2)了解极坐标下平面图形的面积的求法 (3)掌握旋转体体积的求法 (4)会求平面曲线的弧长

第七章微分方程 (1)掌握变量可分离的方程及一阶线性方程的解法 (2)会解齐次方程,和三种可降阶的微分方程 (3)理解二阶线性微分方程解的结构 (4)掌握二阶常系数齐次线性微分方程的解法 (5)会求自由项形如:Pn(x)ex、e[Pcos@x-+P sin@x] 的二阶常系数非齐次线性微分方程的特解 D习程学院
第七章 微分方程 (1)掌握变量可分离的方程及一阶线性方程的解法 (2)会解齐次方程,和三种可降阶的微分方程 (3) 理解二阶线性微分方程解的结构 (4)掌握二阶常系数齐次线性微分方程的解法 (5)会求自由项形如: 的二阶常系数非齐次线性微分方程的特解. ( ) cos sin x x P x e e P x P x m l n 、 +
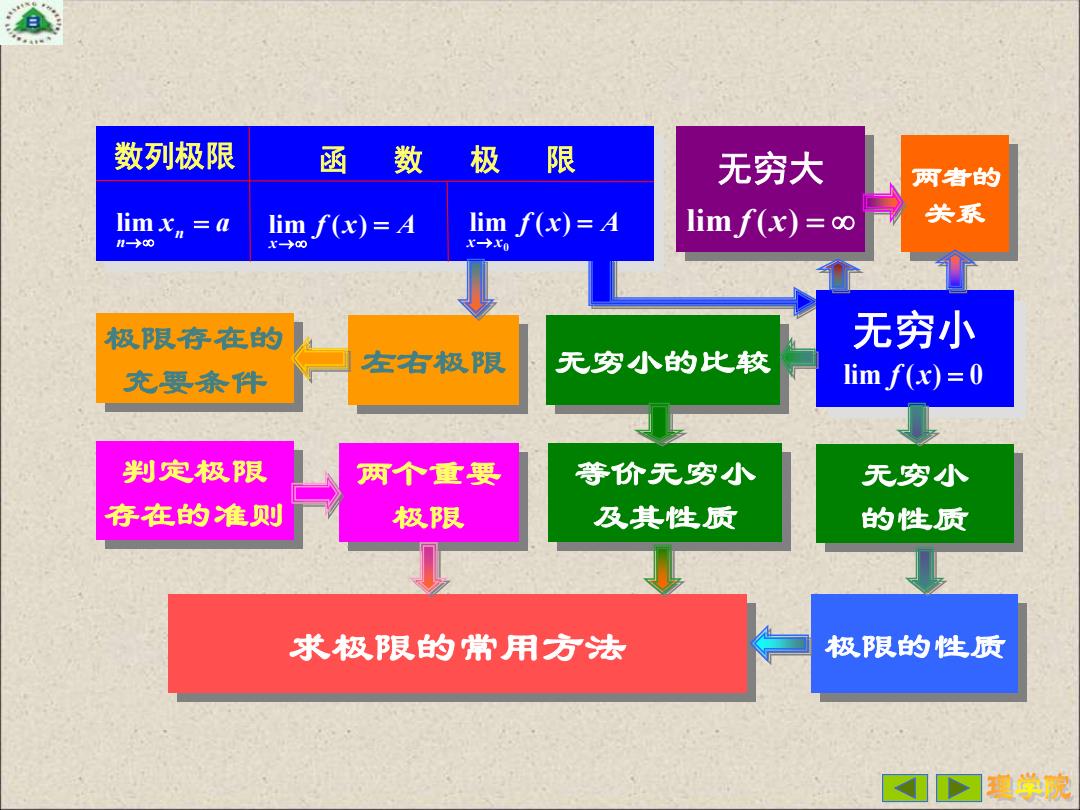
数列极限 函数极限 无穷大 两者的 lim x,=a lim f(x)=A lim f(x)=A lim f(x)=co 关系 n-→0 X->oo x→x0 极限存在的 无穷小 左右极限 无穷小的比较 充要条件 lim f(x)=0 判定极限 两个重要 等价无穷小 无穷小 存在的准则 极限 及其性质 的性质 求极限的常用方法 极限的性质 个少程学院
左右极限 两个重要 极限 求极限的常用方法 无穷小 的性质 极限存在的 充要条件 判定极限 存在的准则 无穷小的比较 极限的性质 数列极限 函 数 极 限 xn a n = → lim f x A x x = → lim ( ) 0 f x A x = → lim ( ) 等价无穷小 及其性质 无穷小 lim f (x) = 0 两者的 关系 无穷大 lim f (x) =
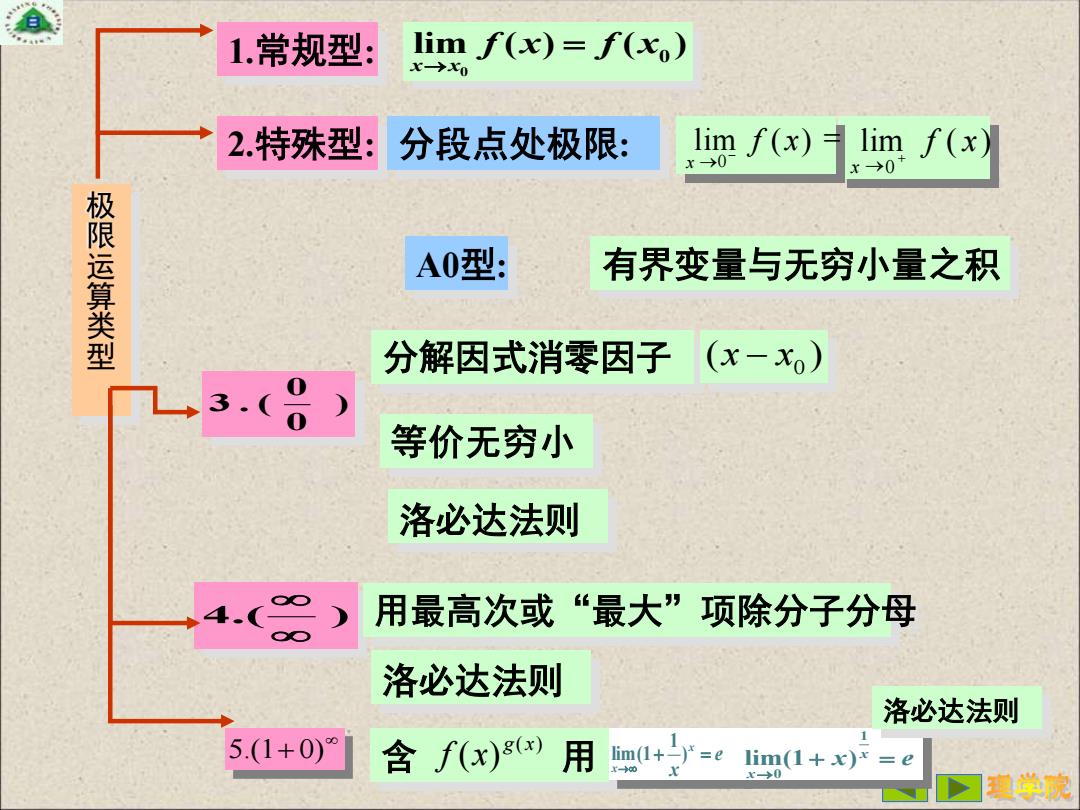
1.常规型 lim f(x)=f(o) x→x0 2.特殊型: 分段点处极限: lim f(x)lim f(x) x->07 x→0 极限运算类型 A0型: 有界变量与无穷小量之积 分解因式消零因子 (x-x) 3 8) 等价无穷小 洛必达法则 用最高次或“最大”项除分子分母 洛必达法则 洛必达法则 5.(1+0)° 含f(x)3) 用 lim(1+)*=e lim(1+x)*=e -00 0 程学院
含 用 极 限 运 算 类 型 1.常规型: 0 0 lim ( ) ( ) x x f x f x → = 2.特殊型: 分段点处极限: A0型: 有界变量与无穷小量之积 ) 0 0 3 .( 分解因式消零因子 ( ) 0 x − x 4.( ) 用最高次或“最大”项除分子分母 等价无穷小 5.(1+ 0) ( ) ( ) g x f x e x x x + = → ) 1 lim(1 x e x x + = → 1 0 lim(1 ) 洛必达法则 洛必达法则 洛必达法则 lim ( ) 0 f x x → + = → − lim ( ) 0 f x x