
函数的可积性 第五章 单变量函数的积分学 假定在区间[,b]上的函数f(x)是有界的,并设其上确界和下确界 分别是M和m,则m≤f(x)≤M,x∈[a,b], 对于区间[,b]的任意一个分割T:a=x,<x<…<x,=b,设函数 f(x)在区间[x1,x]上的上、下确界分别为 M,=sup{f:x∈[x-,x]},m=inf(x):x∈[x,x]} 并记 w=M-m;o=M,-m(1≤i≤n), 分别称为f(x)在区间[a,b]和[x1,x]上的振幅 2
2 函数的可积性 第五章 单变量函数的积分学 分别称为 在区间 假定在区间 上的函数 是有界的,并设其上确界和下确界 分别是 和 则 对于区间 的任意一个分割 设函数 在区间 上的上、下确界分别为 并记 和 上的振幅

函数的可积性 第五章 单变量函数的积分学 对于前面给定的有界函数f(x)和区间[a,b]的分割,和式 5(T=∑MAx,ST=∑mA i=l i=l 分别称之为函数f(x)的Darboux上和与Darboux下和. 显然,对于任意的点5∈[x,x],有 m≤m≤f(5)≤M≤M,i=l,…,n 因此函数f(x)的任意-个Riemann和,S(T)=∑f()△x一定介于 i= 它的Darboux.上和与Darboux下和之间,而且三种和都是有界的: m(b-a)≤S(T≤S(T)≤S(T)≤M(b-a 3
3 函数的可积性 第五章 单变量函数的积分学 对于前面给定的有界函数 和区间 的分割,和式 分别称之为函数 的Darboux上和与Darboux 下和. 显然,对于任意的点 有 因此函数 的任意一个Riemann和 它的Darboux上和与Darboux下和之间,而且三种和都是有界的: 一定介于
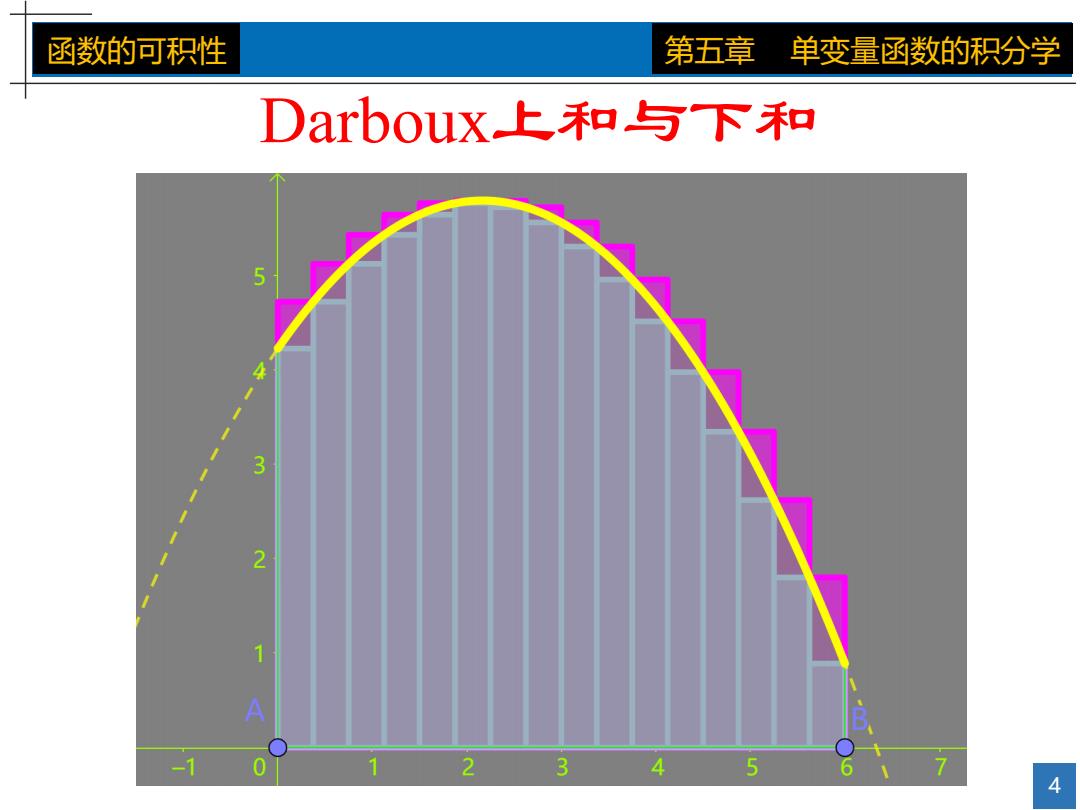
函数的可积性 第五章 单变量函数的积分学 Darb0uX上和与下和 5 3 2 1 A -1 0 1 23 45 6 4
4 函数的可积性 第五章 单变量函数的积分学 Darboux上和与下和

函数的可积性 第五章 单变量函数的积分学 现在考虑分割的变化对Darboux?和的影响.注意到,如果T是分割 T中增加一个分割点x形成的分割,即 T:a=<X<<xk1<x<<x,=b, T:q=x<x<.<x<xp<x<.<X=b. 则①S(T-S(T)=M(K-x)-M1(xe-x)-M2(xe-xx) =(M-Mx-x-1)+(M-M2x-e)≥0. ②S(T)-S(T≤M(&-x-)-1,(xx-x-i)-m(x-xe) =(M:-m.)(xe-x1)+(M:-m)(x-x)swT 即有:0≤5(T)-S(T)≤wW7 同理可得,插入一个节点时,0≤S(T)-ST)≤WT 5
5 函数的可积性 第五章 单变量函数的积分学 现在考虑分割的变化对Darboux和的影响. 注意到,如果 是分割 中增加一个分割点 形成的分割, 即 则 ① ② 即有: 同理可得,插入一个节点时

函数的可积性 第五章 单变量函数的积分学 在分割T的基础上增加一个节点得到分割T',两者的Darbouxa和 满足: 0≤5(T-S(T)≤wT: 0≤S(T)-S(T)≤wWT: 更一般地,设T新增1个节点,加密到T,则 0≤S(T-S(T)≤hwT 0≤S(T)-S(T)≤WT. 加密分割,上和不增,下和不减.Danx和对分割具有“单调性”, 6
6 函数的可积性 第五章 单变量函数的积分学 在分割 的基础上增加一个节点得到分割 两者的Darboux和 满足: 更一般地,设 新增 个节点,加密到 则 加密分割,上和不增,下和不减. Darboux和对分割具有“单调性

函数的可积性 第五章 单变量函数的积分学 f6=0x+20- 积分 25.28 6 上 和:34.72 下和:5.33 5 3 2 1 A 2 -1 0 1 2 3 4 5 6 7 7
7 函数的可积性 第五章 单变量函数的积分学 积 分: 25.28

函数的可积性 第五章 单变量函数的积分学 对于区间[☑,b]的任意两个分割T和T,将两个分割的分割点合起 来形成一个新的分割T,则T既是对T,的加密,也是对T,的加密 于是: S(T)≤S(T)≤S(T)≤S(T,) 即有:一个分割对应的下和,总是不超过另一个分割对应的上和: 定义:记T=infS(T),I=supS(T),分别称为f(x)的下积分 和上积分. 定理:设f(x)有界,则imS()=7,即S(T)=L TI->0 8
8 函数的可积性 第五章 单变量函数的积分学 对于区间 的任意两个分割 和 将两个分割的分割点合起 来形成一个新的分割 则 既是对 的加密,也是对 的加密, 于是 : 即有: 一个分割对应的下和,总是不超过另一个分割对应的上和. 定义 : 记 分别称为 的下积分 和上积分. 定理 : 设 有界,则

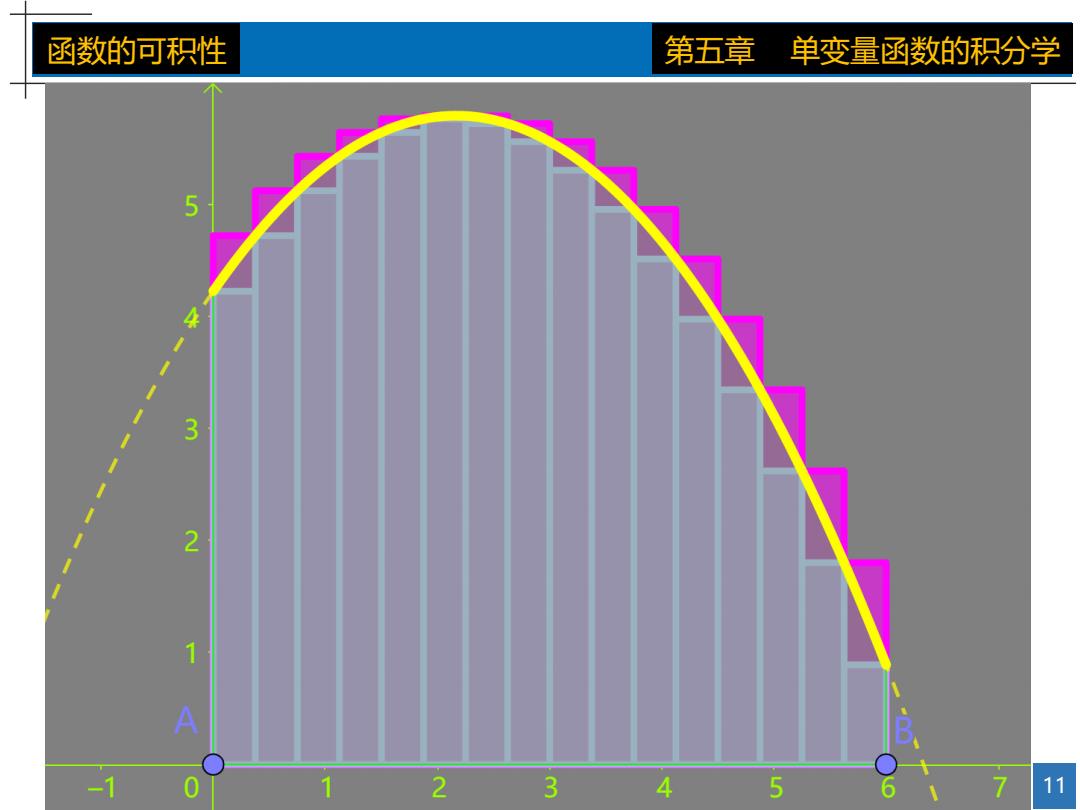
函数的可积性 第五章 单变量函数的积分学 定理:设f(x)在[a,b]上有界,则f(x)在[a,b]上可积当且仅当 7-I=1im(S(T)-ST))=0. 几何意义:Darboux上和与下和的差就是那些正好覆盖函数图像的 一些小矩形的面积之和.若随着分割的加密它趋于零(即,函数图像 的面积为零),函数就是可积的. 定理:设f(x)在[a,上可积台1im∑o,△x,=0.其中0,为 1T→0 i=1 f(x)在分割T的小段[x-1,x]上的振幅 10
10 函数的可积性 第五章 单变量函数的积分学 定理 : 设 在 上有界,则 在 上可积当且仅当 定理 : 设 在 上可积 其中 为 在分割 的小段 上的振幅. 几何意义: Darboux上和与下和的差就是那些正好覆盖函数图像的 一些小矩形的面积之和. 若随着分割的加密它趋于零 (即, 函数图像 的面积为零),函数就是可积的
函数的可积性 第五章 单变量函数的积分学 5 4 3 2 1 A -1 0 2 3 4 5 7 11
11 函数的可积性 第五章 单变量函数的积分学

函数的可积性 第五章 单变量函数的积分学 定理:连续函数都可积:f(x)∈C[a,b]→f(x)∈R[a,b]: 定理:若f(x)在[a,b]上只有有限个间断点,则f(x)在[a,b上 可积 定理:若f(x)在[a,b]上单调,则f(x)在[a,b]上可积 13
13 函数的可积性 第五章 单变量函数的积分学 定理 : 连续函数都可积 : 定理 : 若 在 上只有有限个间断点,则 在 上 可积. 定理 : 若 在 上单调,则 在 上可积