
中国辩空我术大学 University of Science and Technology of China 第五章单变量函数的积分学 §5.1 定积分 §5.2 函数的可积性 §5.3 积分的应用 育創 §5.4反常积分 天下 寰宇 英 學 题 府
1 定积分 第五章 单变量函数的积分学 第五章 单变量函数的积分学 §5.1 定积分 §5.2 函数的可积性 §5.3 积分的应用 §5.4 反常积分

定积分 第五章 单变量函数的积分学 几个典型的定积分问题 1.曲边梯形的面积 y=f(x) 曲边梯形是由连续曲线 y=f(x)(f(x)≥0) X轴以及两直线x=a,x=b a b X 所围成,求其面积A. h l 矩形面积 三角形面积 多边形面积 A=Ih A=二1h A=4+4+4+A 2
2 定积分 第五章 单变量函数的积分学 曲边梯形是由连续曲线 X轴以及两直线 所围成 ,求其面积 A . 矩形面积 三角形面积 多边形面积 1.曲边梯形的面积 几个典型的定积分问题 X Y
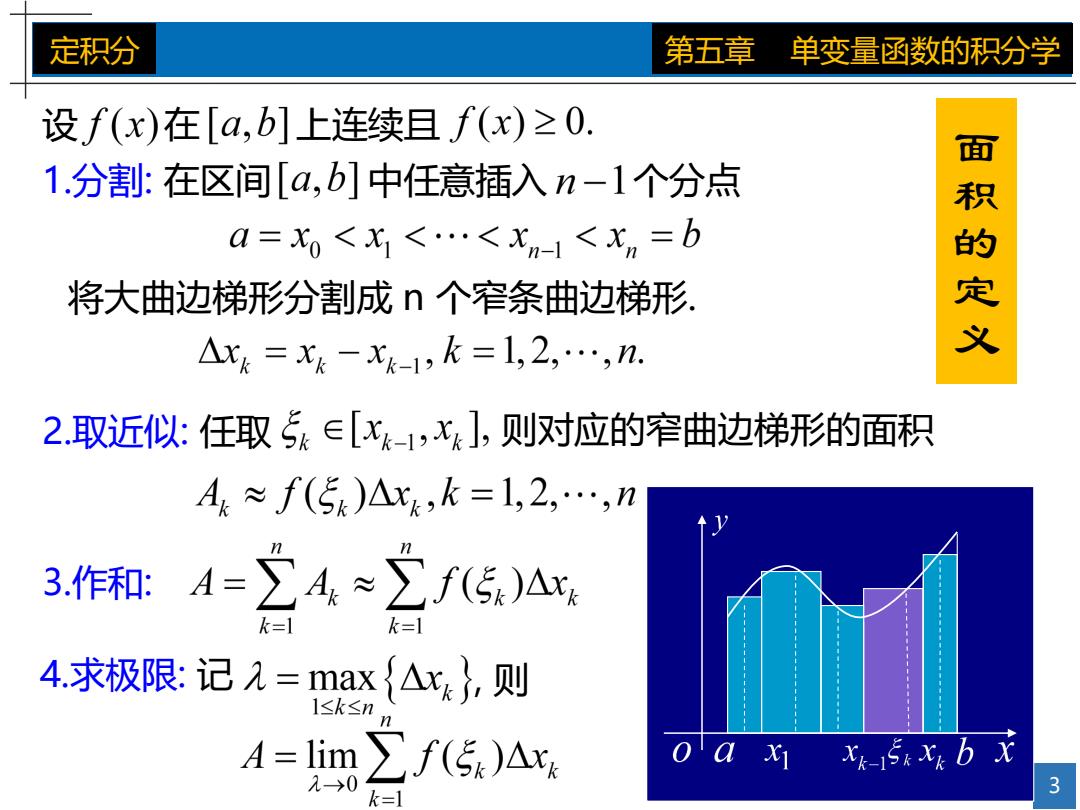
定积分 第五章 单变量函数的积分学 设f(x)在[a,b]上连续且f(x)≥0. 1.分割:在区间[a,b]中任意插入n-1个分点 a=七0<X1<<Xn-1<xn=b 将大曲边梯形分割成n个窄条曲边梯形. 面积的定义 △xk=Xk-xk-1,k=1,2,…,n. 2.取近似:任取5∈[x-1,x],则对应的窄曲边梯形的面积 A≈f(5)△xk,k=1,2,…,n 3.作和:A=∑4≈∑f(5)△x k=1 k=1 4.求极限:记元=max{△x},则 l≤k≤n A=lim∑f(5)△x XK-15kxb x
3 定积分 第五章 单变量函数的积分学 1.分割: 在区间 中任意插入 个分点 将大曲边梯形分割成 n 个窄条曲边梯形. 2.取近似: 任取 则对应的窄曲边梯形的面积 3.作和: 4.求极限: 记 , 则 设 在 上连续且 面 积 的 定 义

定积分 第五章 单变量函数的积分学 2变速直线运动的位移 某物体作变速直线运动,设速度v(t)∈C[T,T,],求这段时间内 物体经过的位移S. (1)分割:在区间[T,T,]中任意插入n-1个分点 H=t<<.<I<=12 记△tk=tk-tk-1,k=1,2,…,n. (2)取近似任取k∈[1k-1,t],则对应该时段上的位移 △Sk≈v(tk)△tk,k=1,2,…,n (3)作和: s=∑△s≈∑)A: 4④求极限:记入=ax{A,}则s=m∑(:)A4: 4
4 定积分 第五章 单变量函数的积分学 2.变速直线运动的位移 (1)分割: 在区间 中任意插入 个分点 (2)取近似: 任取 则对应该时段上的位移 (3)作和: (4)求极限: 记 ,则 某物体作变速直线运动,设速度 求这段时间内 物体经过的位移 . 记

定积分 第五章 单变量函数的积分学 3.变力沿直线做功 某物体受同向变力沿力的方向移动1,受力F=F(S)∈C[0,] 求变力所做的功w. (1)分割:在区间[0,]中任意插入n-1个分点 0=S0<S1<…<Sm-1<Sn=l 记ASk=Sk-Sk-1,k=1,2,…,n (2)取近似:任取5k∈[Sk-1,Sk],则对应该时段上的位移 △wk≈F(5k)△Sk,k=1,2,…,n (3)作和: w=∑Aw≈∑F(5)A 4④求极限:记=max{As:,则w=m∑F(5)A 5 k=1
5 定积分 第五章 单变量函数的积分学 3.变力沿直线做功 (1)分割: 在区间 中任意插入 个分点 (2)取近似: 任取 则对应该时段上的位移 (3)作和: (4)求极限: 记 ,则 某物体受同向变力沿力的方向移动 受力 求变力所做的功 . 记

定积分 第五章 单变量函数的积分学 上述几个问题具有两个共同的基本特征: ()所求总量等于各小区间上的部分量之和; (2)所求部分量近似等于某常量与对应区间长度之乘积. 解决问题方法的共性: (1)解决问题的步骤相同 分割 →近似→求和→取极限 (2)所求量的结构式相同 A=lim ∑f5)Ax,s=1im∑v(z)At:, 2→0 k=1 1→0 k= W=lim∑F(5A)△s: →0 k=1 6
6 定积分 第五章 单变量函数的积分学 上述几个问题具有两个共同的基本特征: (1)所求总量等于各小区间上的部分量之和; (2)所求部分量近似等于某常量与对应区间长度之乘积. 解决问题方法的共性: (1)解决问题的步骤相同 分割 近似 求和 取极限 (2)所求量的结构式相同

定积分 第五章 单变量函数的积分学 定积分的定义 定义:设函数f(x)在[a,b]上有定义,对[a,b]的任意一个分割 T:a=00,36>0,st.对任意满足T<δ的[a,b]的分 割T和任意气∈[xx]有立f(,)A,-<6,则称f四)在 k=1 [a,b]上((Riemann)可积,且积分值为I,记为I=∫心f(x)dx 即:fx)de1im∑f5)△x T→0 K= 7
7 定积分 第五章 单变量函数的积分学 称为分割 的分割宽度. 定积分的定义 定义: 设函数 在 上有定义,对 的任意一个分割 记 再在每个分割的区间上选 可得到Riemann和 若实数 使得: 对任意满足 的 的分 割 和任意 有 则称 在 上(Riemann)可积,且积分值为 ,记为 即:

定积分 第五章 单变量函数的积分学 积分上限 [a,b]称为积分区间 f(x)dx=lim ∑f(5)△x T→0 i=1 积分下限 被积函数 被积表达式 积分变量 黎曼和 注 (1)定积分仅与被积函数及积分区间有关,与极限过程中分割T和点5,的选取 方式无关 (2)在已知函数可积的前提下,可以选择特殊的分割T和点5来计算定积分, (3)积分的值与变元名字无关,即f()dx=∫。fudl=∫f)du 8
8 定积分 第五章 单变量函数的积分学 积分上限 积分下限 被 积 函 数 被 积 表 达 式 积 分 变 量 黎 曼 和 (1) 定积分仅与被积函数及积分区间有关,与极限过程中分割 和点 的选取 注: 方式无关. (2) 在已知函数可积的前提下,可以选择特殊的分割 和点 来计算定积分. (3) 积分的值与变元名字无关,即
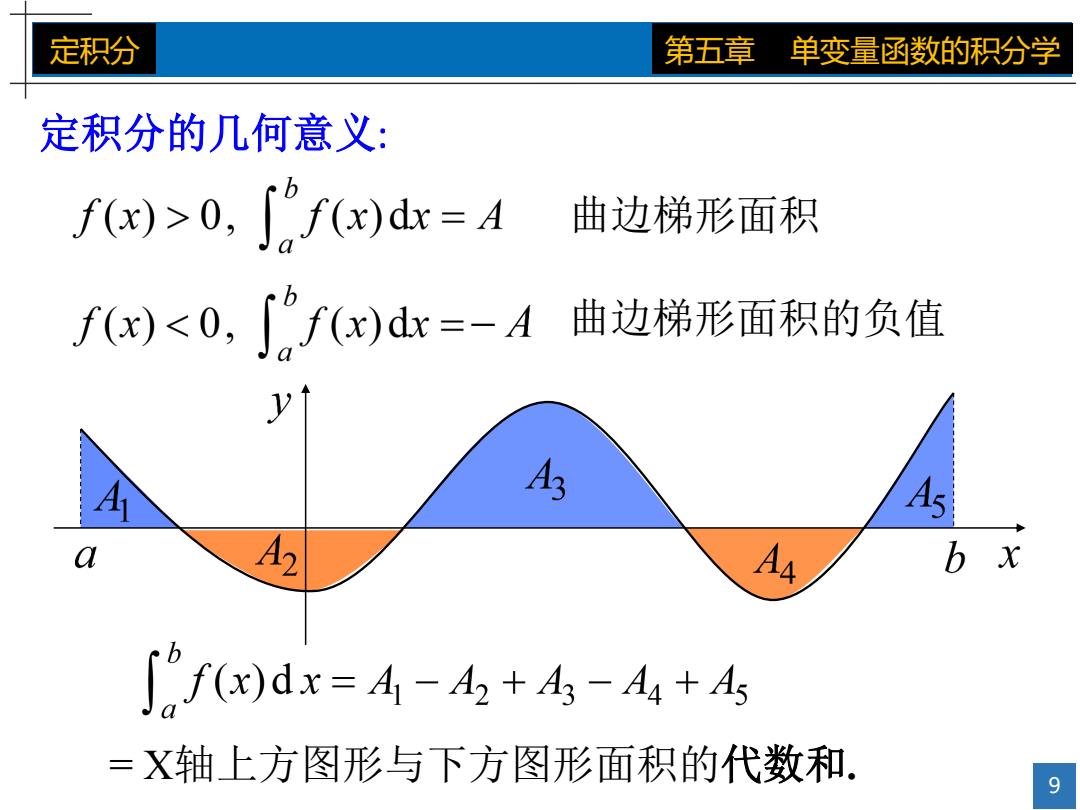
定积分 第五章 单变量函数的积分学 定积分的几何意义: f(x)>0,∫2f(x)d=A 曲边梯形面积 fx)<0,∫f)dr=-A 曲边梯形面积的负值 y A2 b x ∫f)dx=4-+4-A4+4 =X轴上方图形与下方图形面积的代数和. 9
9 定积分 第五章 单变量函数的积分学 定积分的几何意义: 曲边梯形面积 曲边梯形面积的负值 = X轴上方图形与下方图形面积的代数和

定积分 第五章 单变量函数的积分学 问题:什么样的函数Riemann可积,怎么计算定积分? 定理:若函数f(x)在[a,b]上可积,则f(x)在[a,b]上有界 反之,有界未必可积,例如Dirichlet函数不可积. 定理:若函数f(x)在[a,b]上连续,则f(x)在[a,b]上可积, 甚至,若f(x)在[a,b]上有界,且至多只有有限多个间断点,则 f(x)在[a,b]上可积 定理:若函数f(x)在[a,b]上单调,则f(x)在[a,b]上可积 定理(Lebegue):有界函数f(x)在[a,b]上可积,当且仅当f(x) 在[a,b]上几乎处处连续 10
10 定积分 第五章 单变量函数的积分学 问题: 什么样的函数Riemann可积,怎么计算定积分? 定理: 若函数 在 上可积,则 在 上有界. 反之,有界未必可积,例如Dirichlet函数不可积. 定理: 若函数 在 上连续,则 在 上可积. 甚至,若 在 上有界,且至多只有有限多个间断点,则 在 上可积. 定理: 若函数 在 上单调,则 在 上可积. 定理(Lebegue): 有界函数 在 上可积,当且仅当 在 上几乎处处连续