
ch8多元函数微分法及其应用 §1多元函数的基本概念 多元函数的概念 二元函数的极限 二元函数的连续性
多元函数的概念 二元函数的极限 二元函数的连续性

一、多元函数的概念 1.定义 例1V=πr2h r,h(r>0,h>0)可独立取 值,取定一对值,V随之确定· 例2 电流通过电阻所作的功 P与R,I,t P=I2Rt I,t,R可独立取值,取定一组值,P随之 确定
1.定义 , , . , ( 0, 0) 2 值 取定一对值 随之确定 可独立取 V V r h r h r h . , , , , , , 2 确定 可独立取值 取定一组值 随之 电流通过电阻所作的功 与 I t R P P I Rt P R I t 一、多元函数的概念 例1 例2

定义(二元函数) 设有变量x,y和z,若当x,y在一定范围内 任意取定一对值,量按照一定法则,总有 确定的数值与它们对应则称z是x,y的 二元函数. 记作z=f(x,y,或z=z(x,y) 其中:x,y--称为自变量.z--因变量, x,y的变化范围--定义域D zz=f(x,y),(x,y)∈D}值域
. , , , , , , , 二元函数 确定的数值与它们对应 则称 是 的 任意取定一对值 量 按照一定法则 总有 设有变量 和 若当 在一定范围内 z x y z x y z x y 值域 的变化范围 定义域 其中 称为自变量 因变量 z z f x y x y D x y D x y z | ( , ), ( , ) , : , . . 定义(二元函数) 记作z f x, y,或z zx, y~~~~~~~~~~~~ ~~~~~~~~~~ ~~~~~~ ~~~~~~ ~~~~~~

注 ()可类似定义三元函数u=f(x,y,z) 以及三元以上的函数. 例2表明P是R,I,t的函数. 二元及二元以上函数统称为多元函数 (2)数轴上的点←→实数x U=f(x) 平面上的点→(x,y)→U=f(x,y) 空间上的点(x,y,z)U=f(x,,z) 可统一简记为U=f(P),称为点P的函数
注 . (1) , , 以及三元以上的函数 可类似定义三元函数 u f x y z 例2表明P是R,I,t的函数. 二元及二元以上函数统称为多元函数. ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ (2)数轴上的点 实数x U f ( x) 可统一简记为U f P,称为点P的函数. 平面上的点 x, y U f (x, y) 空间上的点 x, y,z U f x, y,z ~~~~~~~~~~~

2.定义域的求法 二元函数z=f(x,y)的定义域D求法: 一切使算式有意义的变量x,y所确定的 点的集合即具有某种意义的点的全体) 例3z=√1-x2-y2 解1-x2-y2≥0,即x2+y2≤1 X 记D:x2+y2≤1 或D={(x,yx2+y2≤1} D:x2+y2≤1
2.定义域的求法 二元函数 z f ( x, y)的定义域 D求法: . , 点的集合即具有某种意义的点的全体 一切使算式有意义的自变量x y所确定的 2 2 例3 z 1 x y 1 0, 1 2 2 2 2 解 x y 即x y , 1 : 1 2 2 2 2 D x y x y D x y 或 记 x y o : 1 2 2 D x y

例4 :=及n(r+月 解 1 x>0; In(x+y) x+y>0 或D={(,)川x>0,y>-x}
ln 0 0; 1 x y x y x x x y x z ln 1 例4 解 x y o y x x D 0 : D x y x y x y x x D , 0, 0 : 或

3.一些概念 邻域以P(x,y为中心6>0为半径的圆的内 部点的全体一点P的6邻域记U(P,6) ppo<δ 即V(,6)=x,yx-xP+-}<6y 内点设E为平面点集,点P∈E, 且存在U(P,6)cE, P就称为E的内点. 开集若E的点都是内点,则称之开集(例4)
3.一些概念 , , 0 0 0 0 0 0 P U P P x y 部点的全体 — 点 的 邻域记 邻域 以 为中心 为半径的圆的内 , { , } 0 2 2 0 2 0 0 pp P 即U P x y x x y y . , , , , 就称为 的内点 且存在 设 为平面点集 点 P E U P E E P E 内点 开集 若E的点都是内点 ,则称之开集 例4. P0 E P

边界 如果点P的任一个邻域内既有属于E的点, 也有不属于E的点(点P本身可以属于E, 也可以不属于E),则称P为E的边界点, E的边界点的全体称为E的边界. 例3圆周x2+y2=1为 D:x2+y2<1的边界 连通性设D是开集. 如果对于D内 任何两点,都可用折线连结 起来,且该折线上的点都属 于D,则称开集D是连通的
也可以不属于 ),则称 为 的边界点. 也有不属于 的点(点 本身可以属于 , 如果点 的任一个邻域内既有属 于 的点, E P E E P E P E D E 的边界点的全体称为 E 的边界. 于 ,则称开集 是连通的. 起来,且该折线上的点 都属 任何两点,都可用折线 连结 设 是开集.如果对于 内 D D D D : 的边界 例 圆周 为 1 3 1 2 2 2 2 D x y x y ~~~~~~ ~~~~ 边界 E P ~~~~~~ 连通性
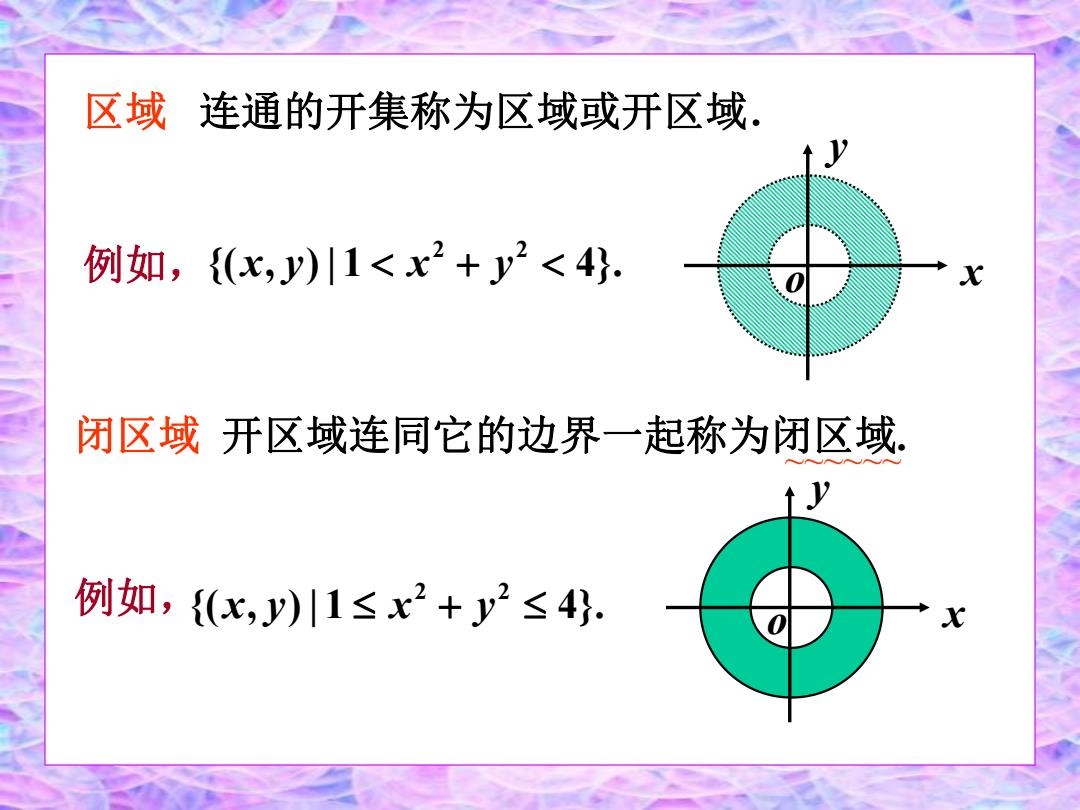
区域 连通的开集称为区域或开区域, 例如,{(x,y)川1<x2+y2<4. X 闭区域开区域连同它的边界一起称为闭区域. 例如,{(x,y)川1≤x2+y2≤4
区域 连通的开集称为区域或开区域. {( , ) | 1 4}. 2 2 例如, x y x y x y o {( , ) | 1 4}. 2 2 例如, x y x y x y o 闭区域 开区域连同它的边界一起称为闭区域. ~~~~~~
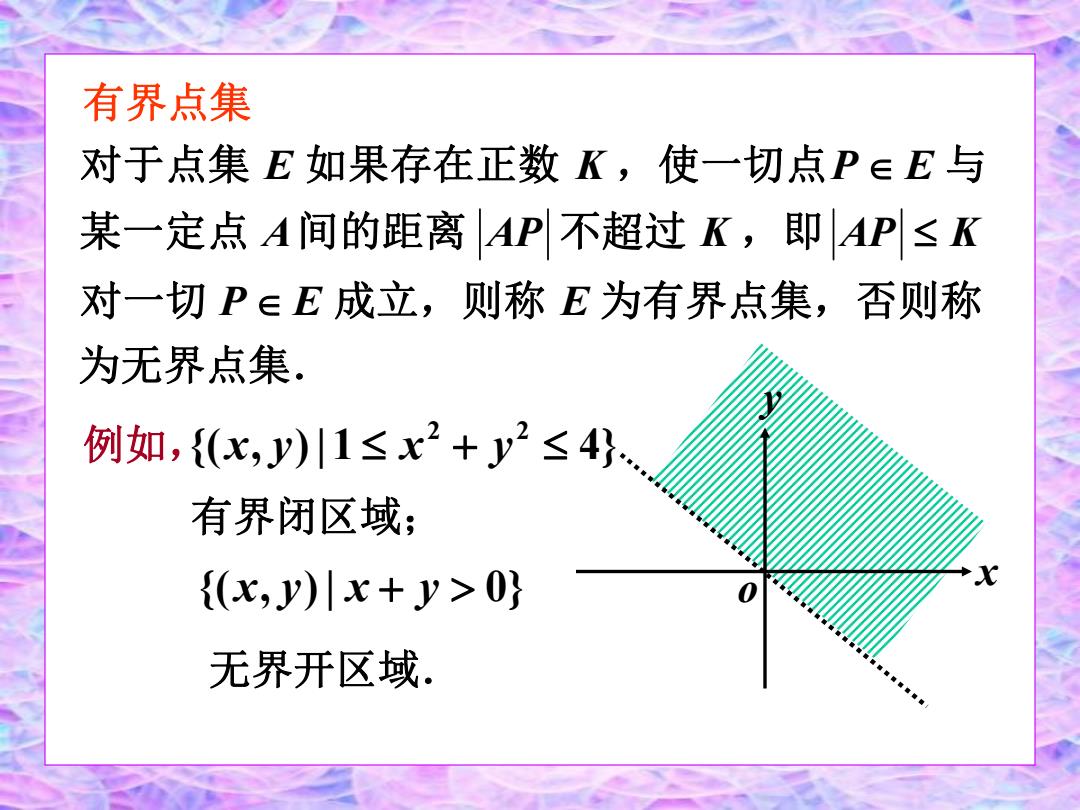
有界点集 对于点集E如果存在正数K,使一切点P∈E与 某一定点A间的距离AP不超过K,即AP≤K 对一切P∈E成立,则称E为有界点集,否则称 为无界点集。 例如,{(x,y)川1≤x2+y2≤4} 有界闭区域; (x,y)x+y>0} 无界开区域
为无界点集. 对一切 成立,则称 为有界点集,否则称 某一定点 间的距离 不超过 ,即 对于点集 如果存在正数 ,使一切点 与 P E E A AP K AP K E K P E {( x, y)| x y 0} 有界闭区域; 无界开区域. x y o 例如,{( , )|1 4} 2 2 x y x y 有界点集