
中国辩空我术大学 University of Science and Technology of China 第六章常微分方程初步 §6.1 一阶微分方程 §4.2 二阶线性微分方程 育 創 天下 寰宇 英 學 府
1 一阶ODE 第六章 常微分方程初步 第六章 常微分方程初步 §6.1 一阶微分方程 §4.2 二阶线性微分方程

一阶ODE 第六章 常微分方程初步 基本概念 定义:含有自变量x,未知函数y以及其导数或微分的关系式称为 常微分方程,简称ODE(Ordinary Differential Equation). 在微分方程中,未知函数导数的最高阶数称为该微分方程的阶· 下面是一些常微分方程的例子. y'=f(x). dy =1+y2 d x dy+ay=0(其中a为常数) xdx+ydy =0. d x2 2
2 一阶ODE 第六章 常微分方程初步 定义: 含有自变量 未知函数 以及其导数或微分的关系式称为 在微分方程中,未知函数导数的最高阶数称为该 微分方程的阶. 下面是一些常微分方程的例子. (其中 为常数) 基本概念 常微分方程,简称ODE(Ordinary Differential Equation)

一阶ODE 第六章 常微分方程初步 般的n阶微分方程的形式为 F(x,y,y',…,y)=0 特别地,称下面的n阶常微分方程 y(+a(x)y(+...+a(x)y'+ao(x)y=f(x) 为n阶线性微分方程(LOD);若f(x)≡O,则称此LODE是齐次的, 否则,称它是非齐次的 dy=ky, iy-x. dy =1+y2, dx d x2 dx 3
3 一阶ODE 第六章 常微分方程初步 一般的 阶微分方程的形式为 为 阶线性微分方程(LODE);若 则称此LODE是齐次的, 特别地,称下面的 阶常微分方程 否则,称它是非齐次的

一阶ODE 第六章 常微分方程初步 定义:设函数p(x)满足 F(x,p(x),p'(x),…,pm(x)≡0(x∈I) 则称y=(x)为方程 F(x,y,y',…,ym)=0 在I上的一个解;包含个相互独立的任意常数的解称为 方程的通解;不含任意常数的解称为特解. 例如,对微分方程y”+a2y=0: y=sin ax,y=c0Sax是两个特解; y=(C,+C2)sinax,y=Ce9 cos ax是解,但不是通解. y=C1 sinax+C2 cos ax是通解. 4
4 一阶ODE 第六章 常微分方程初步 定义: 设函数 满足 则称 为方程 在 I 上的一个解; 包含 个相互独立的任意常数的解称为 方程的通解; 是通解. 例如,对微分方程 是解,但不是通解. 是两个特解; 不含任意常数的解称为特解

一阶ODE 第六章 常微分方程初步 注意:通解未必包含所有的解 例如,y(x)=sin(x+C)是方程(y')2+y2=1的通解 y=±1也是该方程的解,但通解不包含y=±1. 实际问题中,微分方程的解通常还要满足一些条件,这些条件称为 定解条件 常用的定解条件是初始条件,即指定阶微分方程的解在某一点 X=X,满足 y(x)=yo,y'(x)=y0,…,y-(x)=y-. 阶微分方程联合初始条件,称为初值问题或柯西问题 5
5 一阶ODE 第六章 常微分方程初步 注意:通解未必包含所有的解. 是方程 的通解, 也是该方程的解,但通解不包含 例如, 实际问题中,微分方程的解通常还要满足一些条件,这些条件称为 定解条件. n 阶微分方程联合初始条件,称为初值问题或柯西问题. 常用的定解条件是初始条件,即指定 n 阶微分方程的解在某一点 满足:

一阶ODE 第六章 常微分方程初步 可分离变量的一阶ODE 形如 f(x)g(y) dx 的一阶常微分方程称为可分离变量的方程. 解法: ∫布小wa=e:o=叹 例:求下列微分方程的通解。 d y X dx 2.(1+x2)ydy+V1-y2dx=0 y 7
7 一阶ODE 第六章 常微分方程初步 可分离变量的一阶ODE 形如 的一阶常微分方程称为可分离变量的方程 . 例 : 求下列微分方程的通解. dy f x dx g y ( ) ( ) 解法 : y c g c : ( ) 0 .
一阶ODE 第六章 常微分方程初步 齐次一阶ODE 形如 =0 d dx 的一阶微分方程称为齐次的. 解法:令u=卫」 y'=(ux)'=u+xu'=p(u) X →d'=(p(0)-w) 可分离变量ODE 将待解ODE通过变量代换转为已知类型的ODE,是一种常见的 技巧. 8
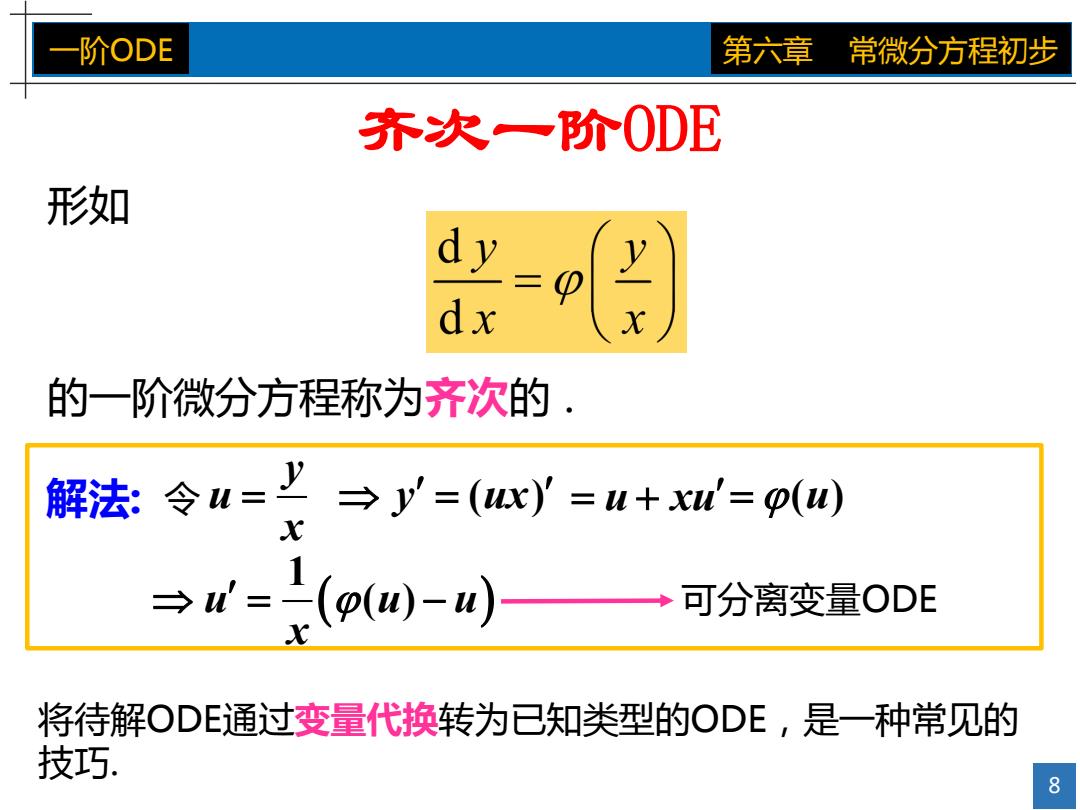
8 一阶ODE 第六章 常微分方程初步 齐次一阶ODE 形如 的一阶微分方程称为齐次的 . y u x 解法: 令 y ux ( ) u xu ( ) u u u u x 1 ( ) 可分离变量ODE 将待解ODE通过变量代换转为已知类型的ODE,是一种常见的 技巧

一阶ODE 第六章 常微分方程初步 例:求下列微分方程的通解. 1 dy x+y dx x-y 2.xdy=(y+y*+y)dx dy-7x+3y+7 3. dx 3x-7y-3 x=X+k dy ax+by+c y=Y+h dY AX+BY dx azx+b2y+c2 dX」 A,X+B,Y 坐标平移 (齐次) 9
9 一阶ODE 第六章 常微分方程初步 例 : 求下列微分方程的通解. (齐次) 坐标平移

一阶ODE 第六章 常微分方程初步 一阶线性ODE 一阶线性ODE标准形式: +2wP=g田"首- 若q(x)=0,称为齐次方程; 若q(x)≠0,称为非齐次方程. 非齐次方程的通解 齐次方程的通解十非齐次方程的特解 >1.求齐次线性方程的通解 >2.找一个非齐次线性方程的特解 10
10 一阶ODE 第六章 常微分方程初步 一阶线性ODE标准形式: 称为非齐次方程. 若 , 称为齐次方程 ; 若 , 一阶线性ODE 2. 找一个非齐次线性方程的特解 1. 求齐次线性方程的通解 非齐次方程的通解 齐次方程的通解 非齐次方程的特解 (“首一”)

一阶ODE 第六章 常微分方程初步 待解方程为: dy+p(x)y=q(x) d L对应的济次方程为:十p少中 其通解为:yn(x)=Cepd 2.用常数变易法求解线性非齐次方程的特解:设 y(x)=C()·eJur 代入方程得: C-Jq)x 11
11 一阶ODE 第六章 常微分方程初步 2. 用常数变易法求解线性非齐次方程的特解:设 待解方程为: 1. 对应的齐次方程为: 其通解为: 代入方程得: