
第三章多维随机变量及其分布 9§3.1二维随机变量 。§3.2边缘分布 §3.3条件分布 。§3.4相互独立的随机变量 §3.5两个随机变量的函数的分布 2/102
2/102 第三章 多维随机变量及其分布 §3.1 二维随机变量 §3.2 边缘分布 §3.3 条件分布 §3.4 相互独立的随机变量 §3.5 两个随机变量的函数的分布
§3.1二维随机变量 定义2.3:设E是一个随机试验,它的样本空间是 S={e},设X=X(e)和Y=Y(e)是定义在S上的随机 变量,由它们构成的一个向量X,Y),叫做二维随 机向量,或二维随机变量 X(e) 2 Y(e) 3/102
3/102 §3.1 二维随机变量 定义2.3: 设E是一个随机试验,它的样本空间是 S={e},设X=X(e)和Y=Y(e)是定义在S上的随机 变量,由它们构成的一个向量(X,Y),叫做二维随 机向量,或二维随机变量 • e •Y(e) • X(e)

§3.1二维随机变量 实例1炮弹的弹着点的位置(X,) 就是一个二维随机变量 实例2考查某一地区学前儿童的 发育情况,则儿童的身高H和 体重W就构成二维随机变量 (H,W) ⊙两个分量是有内在联系的,因 此要将X,Y作为整体来研究 。其性质与X、Y及X,Y之间的关系 均有关,逐个研究X,Y的性质是不 够的。 4/102
4/102 §3.1 二维随机变量 实例1 炮弹的弹着点的位置 (X,Y) 就是一个二维随机变量 实例2 考查某一地 区学前儿童的 发育情况 , 则儿童的身高 H 和 体重 W 就构成二维随机变量 (H,W) 两个分量是有内在联系的,因 此要将X,Y作为整体来研究 ⚫ 其性质与X、Y及X,Y之间的关系 均有关,逐个研究X,Y的性质是不 够的

§3.1二维随机变量 AN 二维随机变量分布函数的定义 定义设(仪,Y)是二维随机变量,对于任意实数x,y, 二元函数: Fxy)=P{X≤x)∩(Y≤y)},记做P{X≤,Y≤y} 称为二维随机变量(X,Y)的分布函数,或称为随机 变量X和Y的联合分布函数。 5/102
5/102 §3.1 二维随机变量 二维随机变量分布函数的定义 定义 设(X,Y)是二维随机变量,对于任意实数x,y, 二元函数: F(x,y)=P{(X≤x)∩(Y≤y)},记做P{X≤x,Y≤y} 称为二维随机变量(X,Y)的分布函数,或称为随机 变量X和Y的联合分布函数

§3.1二维随机变量 ·二维随机变量分布函数的意义 将(X,Y)看成是平面上随机点的坐标,则分布函数F化,y) 在点(化,y)处的函数值是随机点X,Y)落在以(x,)为顶点的 左下方的无穷矩形区域内的概率 随机点落在矩形区域的概率: Pix1<XSx2,y1<YSV2=F(x2V2)-F(x2V)-F(X1)+F(x1V) ↑y (x,y) (1,y2) y2 c2,y2) X≤x,Yy V1 2,y1) c1,1) x X1 X2 6/102
6/102 §3.1 二维随机变量 二维随机变量分布函数的意义 ⚫ 将(X,Y)看成是平面上随机点的坐标,则分布函数F(x,y) 在点(x,y)处的函数值是随机点(X,Y)落在以(x,y)为顶点的 左下方的无穷矩形区域内的概率 ⚫ 随机点落在矩形区域的概率: ⚫ P{x1<X≤x2,y1<Y≤y2 }=F(x2 ,y2 )-F(x2 ,y1 )-F(x1 ,y2 )+F(x1 ,y1 ) o x y (x, y) • X x,Y y y x o x1 x2 y1 y2 (X, Y ) (x2 , y2 ) (x2 , y1 ) (x1 , y2 ) (x1 , y1 )
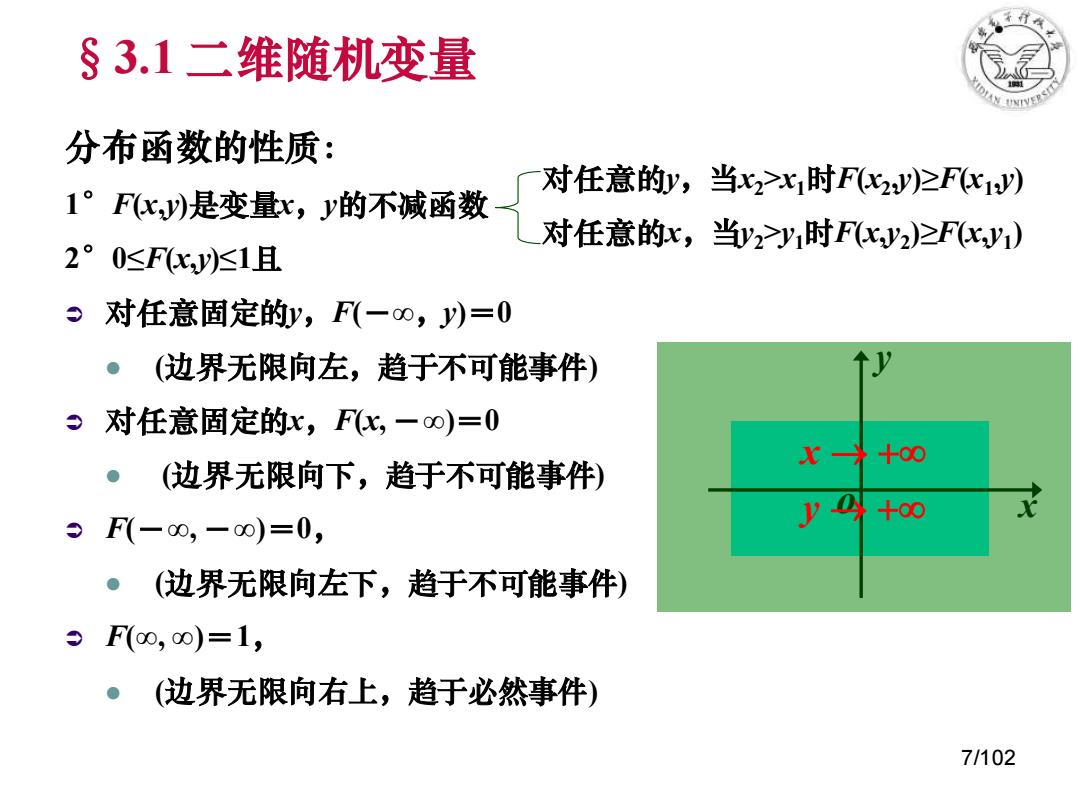
§3.1二维随机变量 分布函数的性质: 对任意的y,当x2>x1时Fx2y)≥Fc1y) 1°Fc,y)是变量,y的不减函数 对任意的,当y2y1时FKy2)≥F(cy1) 2°0sFKy1且 9对任意固定的y,F(一0,y)=0 (边界无限向左,趋于不可能事件) 对任意固定的x,F化,一oo)=0 (边界无限向下,趋于不可能事件) +00 9F(-00,-0)=0, y (边界无限向左下,趋于不可能事件) 9F(0,0)=1, (边界无限向右上,趋于必然事件) 7/102
7/102 §3.1 二维随机变量 分布函数的性质: 1°F(x,y)是变量x,y的不减函数 2°0≤F(x,y)≤1且 对任意固定的y,F(-∞,y)=0 ⚫ (边界无限向左,趋于不可能事件) 对任意固定的x,F(x, -∞)=0 ⚫ (边界无限向下,趋于不可能事件) F(-∞, -∞)=0, ⚫ (边界无限向左下,趋于不可能事件) F(∞, ∞)=1, ⚫ (边界无限向右上,趋于必然事件) o x y → + → + y x 对任意的y,当x2>x1时F(x2 ,y)≥F(x1 ,y) 对任意的x,当y2>y1时F(x,y2 )≥F(x,y1 )

§3.1二维随机变量 3 F(xy)=F(x+0,y),F(xy)=F(x3y+0) ● Fxy)关于x右连续,关于y也右连续 4°对于任意点K1y1),(心2y2),x1x2,y'2, 下述不等式成立: ●Fx2y'2)-Fx2y1)-Fx1y'2)+FK1y1)≥0 。矩形区内的概率,及概率非负性 8/102
8/102 §3.1 二维随机变量 3°F(x,y)=F(x+0,y),F(x,y)=F(x,y+0) ⚫ F(x,y)关于x右连续,关于y也右连续 4°对于任意点(x1 ,y1 ),(x2 ,y2 ),x1<x2,y1<y2, 下述不等式成立: ⚫ F(x2 ,y2 )-F(x2 ,y1 )-F(x1 ,y2 )+F(x1 ,y1 )≥0 ⚫ 矩形区内的概率,及概率非负性

§3.1二维随机变量 o推广到n维: 定义:一般,设E是一个随机试验,它的样本空间是S= {e},设X1=X(e),X2=X2(e),…,Xm=Xn(e)是定义在S 上的随机变量,由它们构成的一个n维向量(X1,X2,…,Xm) 叫做n维随机向量,或n维随机变量 分布函数 定义设(X1,X2,,Xm)是n维随机变量,对于n个任意实数 K1,2,,Xn,n元函数: FK1,X2,,Xn=P{X1≤x1,X2≤x2,…,Xm≤xn} 称为n维随机变量(X1,X2,,X)的分布函数,或称为随机 变量X1,X2)…,Xm的联合分布函数。 。具有同二维类似的性质。 9/102
9/102 §3.1 二维随机变量 推广到n维: ⚫ 定义:一般,设E是一个随机试验,它的样本空间是S= {e},设X1=X1 (e),X2=X2 (e),…,Xn =Xn (e)是定义在S 上的随机变量,由它们构成的一个n维向量(X1 ,X2 , …,Xn ) 叫做n维随机向量,或n维随机变量 分布函数 ⚫ 定义 设(X1 ,X2 , …,Xn )是n维随机变量,对于n个任意实数 x1,x2,…,xn,n元函数: ⚫ F(x1,x2,…,xn )=P{ X1x1 ,X2x2 , …,Xnxn } ⚫ 称为n维随机变量(X1 ,X2 , …,Xn )的分布函数,或称为随机 变量X1 ,X2 , …,Xn的联合分布函数。 具有同二维类似的性质

§3.1二维随机变量 。二维离散型的随机变量: 01 定义:若二维随机变量(X,Y)全部可能取到的不相同的值 是有限对或可列无限多对,则称(X,Y)是离散型随机变量 9二维离散型随机变量的分布律: 设二维离散型随机变量(X,Y)所有可能取的值为化y),i, j=1,2,…, ·记P{X=xY=y}=P,i,=1,2,,则由概率的定义有: PP0,∑∑p,1 i=1 i= 则称P{X=xY=y=P,i,广=1,2,…为二维离散型随机变 量(X,Y)的分布律,或随机变量X和Y的联合分布律 10/102
10/102 §3.1 二维随机变量 二维离散型的随机变量: ⚫ 定义:若二维随机变量(X,Y)全部可能取到的不相同的值 是有限对或可列无限多对,则称(X,Y)是离散型随机变量 二维离散型随机变量的分布律: ⚫ 设二维离散型随机变量(X,Y)所有可能取的值为(xi ,yj ),i, j=1,2,…, ⚫ 记P{X=xi ,Y=yj }=pij,i,j=1,2,…,则由概率的定义有: ⚫ pij≥0, =1 ⚫ 则称P{X=xi ,Y=yj }=pij,i,j=1,2,…为二维离散型随机变 量(X,Y)的分布律,或随机变量X和Y的联合分布律。 = i 1 j=1 pij

§3.1二维随机变量 9也可以用表格的形式给出: X X2 乃 P11 P21 Pa P12 P22 : .:: yj Pu 2 P 11/102
11/102 §3.1 二维随机变量 也可以用表格的形式给出: X Y 1 x 2 x … i x … 1 y 11 p p21 … i1 p … 2 y p12 p22 i2 p … j y j p1 j p2 … ij p …