
内容介绍 三、数理统计 1.Matlab统计工具箱中常见的统计命令 2.直方图和箱线图实验 3.抽样分布实验 4.参数估计和假设检验实验 2/87
2/87 内容介绍 三、数理统计 1. Matlab统计工具箱中常见的统计命令 2. 直方图和箱线图实验 3. 抽样分布实验 4. 参数估计和假设检验实验

Matlab统计工具箱中常见的统计命令 。1、基本统计量 对于随机变量x,计算其基本统计量的命令如下: 均值:mean() 标准差:std(x) 中位数:median(x) 方差:var(x) 偏度:skewness(x)峰度:kurtosis(x) 。2、频数直方图的描绘 oA、给出数组data的频数表的命令为:[N,X灯=hist(data,k) 此命令将区间[min(data),max(data)]分为k个小区间(缺省为1o),返回数组 data落在每一个小区间的频数N和每一个小区间的中点X。 B、描绘数组data的频数直方图的命令为:hist(data,k) 3/87
3/87 Matlab统计工具箱中常见的统计命令 1、基本统计量 对于随机变量x,计算其基本统计量的命令如下: ⚫ 均值:mean(x) 标准差:std(x) ⚫ 中位数:median(x) 方差:var(x) ⚫ 偏度:skewness(x) 峰度:kurtosis(x) 2、频数直方图的描绘 ⚫ A、给出数组data的频数表的命令为:[N,X]=hist(data,k) ⚫ 此命令将区间[min(data),max(data)]分为k个小区间(缺省为10),返回数组 data落在每一个小区间的频数N和每一个小区间的中点X。 ⚫ B、描绘数组data的频数直方图的命令为: hist(data,k)

Matlab统计工具箱中常见的统计命令 93、参数估计 A、对于正态总体,点估计和区间估计可同时由以下命令获得: [muhat,sigmahat,muci,sigmaci]=normfit(x,alpha) 此命令在显著性水平alpha下估计x的参数(alpha缺省值为5%),返回值 muhat是均值的点估计值,sigmahat是标准差的点估计值,muci是均值的区 间估计,sigmaci-是标准差的区间估计。 B、对其他分布总体,两种处理办法:一是取容量充分大的样本,按中 心极限定理,它近似服从正态分布,仍可用上面估计公式计算;二是使 用特定分布总体的估计命令,常用的命令如: [muhat,muci]=expfit(x,alpha) [lam bdahat,lam bdaci]=poissfit(x,alpha) [phat,pci]=weibfit(x,alpha) 4/87
4/87 3、参数估计 ⚫ A、对于正态总体,点估计和区间估计可同时由以下命令获得: ⚫ [muhat,sigmahat,muci,sigmaci]=normfit(x,alpha) ⚫ 此命令在显著性水平alpha下估计x的参数(alpha缺省值为5%),返回值 muhat是均值的点估计值,sigmahat是标准差的点估计值,muci是均值的区 间估计,sigmaci是标准差的区间估计。 ⚫ B、对其他分布总体,两种处理办法:一是取容量充分大的样本,按中 心极限定理,它近似服从正态分布,仍可用上面估计公式计算;二是使 用特定分布总体的估计命令,常用的命令如: ⚫ [muhat,muci]=expfit(x,alpha) ⚫ [lambdahat, lambdaci]=poissfit(x,alpha) ⚫ [phat, pci]=weibfit(x,alpha) Matlab统计工具箱中常见的统计命令

Matlab统计工具箱中常见的统计命令 。4、正态总体假设检验 A、单总体均值的z检验: [h,sig,ci]=ztest(x,m,sigma,alpha,tail) 检验数据x关于总体均值的某一假设是否成立,其中sigmai为已知方差, alpha为显著性水平,究竟检验什么假设取决于tail的取值: tail=0,检验假设“x的均值等于m” tail=1,检验假设“x的均值大于m” tail=-1,检验假设“x的均值小于m” tail的缺省值为0,alpha的缺省值为5%。 返回值h为一个布尔值,h=1表示可拒绝原假设,h=0表示不可拒绝原假 设,sig为假设成立的概率,ci为均值的1-apha置信区间。 5/87
5/87 4、正态总体假设检验 ⚫ A、单总体均值的z检验: ⚫ [h,sig,ci]=ztest(x,m,sigma,alpha,tail) ⚫ 检验数据x关于总体均值的某一假设是否成立,其中sigma为已知方差, alpha为显著性水平,究竟检验什么假设取决于tail的取值: ⚫ tail=0,检验假设“x的均值等于m” ⚫ tail=1,检验假设“x的均值大于m” ⚫ tail=-1,检验假设“x的均值小于m” ⚫ tail的缺省值为0, alpha的缺省值为5%。 ⚫ 返回值h为一个布尔值,h=1表示可拒绝原假设, h=0表示不可拒绝原假 设,sig为假设成立的概率,ci为均值的1- alpha置信区间。 Matlab统计工具箱中常见的统计命令

Matlab统计工具箱中常见的统计命令 ●B、单总体均值的检验: [h,sig,ci]=ttest(x,m,alpha,tail) ●C、双总体均值的t检验: [h,sig,ci]=ttest2(x,y,alpha,tail) 6/87
6/87 ⚫ B、单总体均值的t检验: ⚫ [h,sig,ci]=ttest(x,m,alpha,tail) ⚫ C、双总体均值的t检验: ⚫ [h,sig,ci]=ttest2(x,y,alpha,tail) Matlab统计工具箱中常见的统计命令

Matlab统计工具箱中常见的统计命令 5、非参数检验:总体分布的检验 Matlab统计工具箱提供了两个对总体分布进行检验的命令: 。A、h=normplot(x) 此命令显示数据矩阵x的正态概率图,如果数据来自于正态 分布,则图形显示出直线形态,而其他概率分布函数显示 出曲线形态。 oB、h=weibplot(x) 此命令显示数据矩阵x的Veibull概率图,如果数据来自于 Veibu川分布,则图形显示出直线形态,而其他概率分布函 数显示出曲线形态。 7187
7/87 5、非参数检验:总体分布的检验 ⚫ Matlab统计工具箱提供了两个对总体分布进行检验的命令: ⚫ A、 h=normplot(x) ⚫ 此命令显示数据矩阵x的正态概率图,如果数据来自于正态 分布,则图形显示出直线形态,而其他概率分布函数显示 出曲线形态。 ⚫ B、h=weibplot(x) ⚫ 此命令显示数据矩阵x的Weibull概率图,如果数据来自于 Weibull分布,则图形显示出直线形态,而其他概率分布函 数显示出曲线形态。 Matlab统计工具箱中常见的统计命令

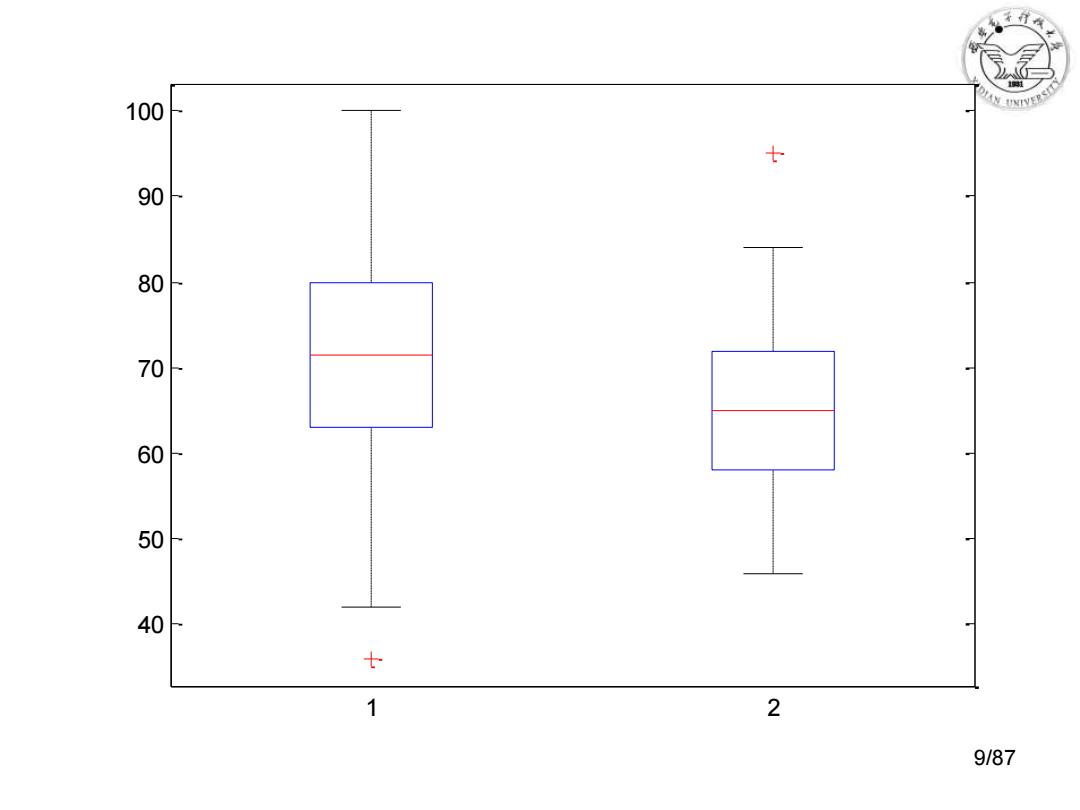
2.直方图和箱线图实验 例1在同一坐标轴上画box图,并对两个班的成绩进行初步 的分析比较。 两个教学班各30名同学,在数学课程上,A班用新教学方法 组织教学,B班用传统方法组织教学,现得期末考试成绩如 下。 A:82,92,77,62,70,36,80,100,74,64,63,56,72,78, 68,65,72.70,58,92,79,92,65,56,85,73,61,71,42,89 B:57,67,64,54,77,65,71,58,59,69,67,84,63,95,81, 46,49,60,64,66,74,55,58,63,65,68,76,72,48,72 解>>clear X=[82,92,77,62,70,36,80,100,74,64,63,56,72,78,68,65,72,70,58,92,79,92,6 5,56,85,73,61,71,42,89;57,67,64,54,77,65,71,58,59,69,67,84,63,95,81,46, 49,60,64,66,74,55,58,63,65,68,76,72,48,72] boxplot(x') 8/87
8/87 例1 在同一坐标轴上画box图,并对两个班的成绩进行初步 的分析比较。 两个教学班各30名同学,在数学课程上,A班用新教学方法 组织教学,B班用传统方法组织教学,现得期末考试成绩如 下。 A:82,92,77,62,70,36,80,100,74,64,63,56,72,78, 68,65,72.70,58,92,79,92,65,56,85,73,61,71,42,89 B:57,67,64,54,77,65,71,58,59,69,67,84,63,95,81, 46,49, 60, 64,66,74,55,58,63,65,68,76,72,48,72 解 >> clear x=[82,92,77,62,70,36,80,100,74,64,63,56,72,78,68,65,72,70,58,92,79,92,6 5,56,85,73,61,71,42,89;57,67,64,54,77,65,71,58,59,69,67,84,63,95,81,46, 49,60,64,66,74,55,58,63,65,68,76,72,48,72]; boxplot(x') 2. 直方图和箱线图实验
100 + 90 80 70 60 50 40 七 1 2 9/87
9/87 40 50 60 70 80 90 100 1 2

从图中直观地看出,两个班成绩的分布是正态(对称) 的,A班成绩较为分散(方差大),B班成绩则较集中(方差 小)。A班成绩明显高于B班(均值比较.并且A班25%低分 段上限接近B班中值线,A班中值线接近B班25%高分段下 限)。A班的平均成绩约为70分(中值),B班约为65分(中值)。 A班有一名同学的成绩过低(离群),而B班成绩优秀的只有 一人(离群)。 需要注意的是,从图中我们不能得出新教学方法一定 优于传统教学方法的结论,因为我们并不知道两个班级原 有的数学基础是怎样的。 10/87
10/87 从图中直观地看出,两个班成绩的分布是正态(对称) 的,A班成绩较为分散(方差大),B班成绩则较集中(方差 小)。A班成绩明显高于B班(均值比较.并且A班25%低分 段上限接近B班中值线,A班中值线接近B班25%高分段下 限)。A班的平均成绩约为70分(中值),B班约为65分(中值)。 A班有一名同学的成绩过低(离群),而B班成绩优秀的只有 一人(离群)。 需要注意的是,从图中我们不能得出新教学方法一定 优于传统教学方法的结论,因为我们并不知道两个班级原 有的数学基础是怎样的

例2用模拟试验的方法直观地验证教材§6.3抽样分布定 理一的结论。 假定变量X~N60,52),用随机数生成的方法模拟 对X的500次简单随机抽样,每个样本的容量为16。利用 这500×16个样本数据直观地验证样本均值X的抽样分布 为均值等于60、方差等于25/16的正态分布,即 X~N60,1.252) 11/87
11/87 例2 用模拟试验的方法直观地验证教材§6.3抽样分布定 理一的结论。 假定变量 ,用随机数生成的方法模拟 对 的500次简单随机抽样,每个样本的容量为16。利用 这500×16个样本数据直观地验证样本均值 的抽样分布 为均值等于60、方差等于25/16的正态分布,即 X X ( ) 2 X ~ N 60,1.25 ( ) 2 X ~ N 60,5