西安电子科技大学：《数学模型》课程教学资源（PPT课件讲稿）优化模型——整数规划

http://Ixy.xidian.edu.cn/shumo/ 2.整数线性规划 整数线性规划建模一引例 整数线性规划模型 整数线性规划的解法 特殊形式的整数规划问题 整数线性规划建模示例

http://lxy.xidian.edu.cn/shumo/ 2. 整数线性规划 整数线性规划建模——引例 整数线性规划模型 整数线性规划的解法 特殊形式的整数规划问题 整数线性规划建模示例

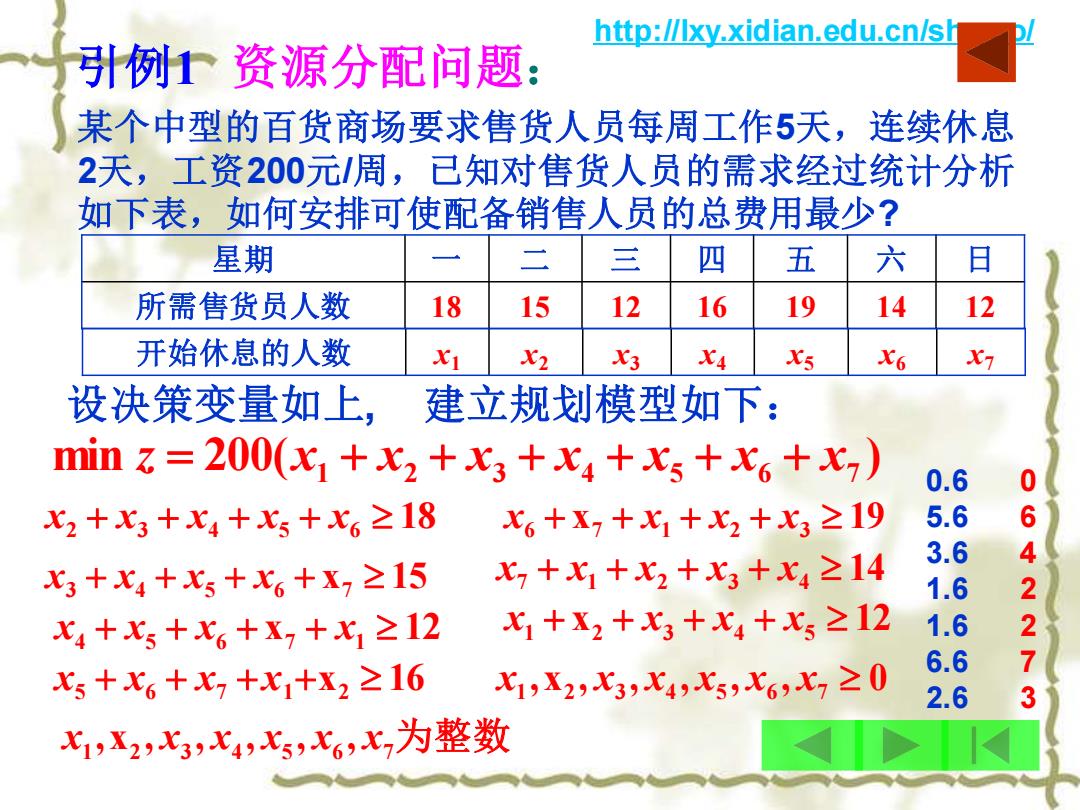
http://Ixy.xidian.edu.cn/sh 引例资源分配问题 某个中型的百货商场要求售货人员每周工作5天，连续休息 2天，工资200元/周，已知对售货人员的需求经过统计分析 如下表，如何安排可使配备销售人员的总费用最少？ 星期 三 四 五 六 日 所需售货员人数 18 15 12 16 19 14 12 开始休息的人数 X1 X2 X3 X4 X5 X6 X7 设决策变量如上，建立规划模型如下： minz=200(x1+x2+x3+x4+xs+x6+x7) 0.6 0 x2+x3+x4+xs+x6≥18 x6+X7+x1+X2+x3≥19 5.6 6 3.6 x3+x4+x5+x6+x7≥15 x7+x1+x2+x3+x4≥14 1.6 2 x4+x5+x6+x2+X1≥12 x1+X2+x3+x4+x5≥12 1.6 2 x5+x6+x7+x1+x2≥16 1,X2X3x4x5,X6,X7≥0 6.6 7 2.6 3 七1，X2七3X4,七，X6,七7为整数

http://lxy.xidian.edu.cn/shumo/ 某个中型的百货商场要求售货人员每周工作5天，连续休息 2天，工资200元/周，已知对售货人员的需求经过统计分析 如下表，如何安排可使配备销售人员的总费用最少? 引例1 资源分配问题： 星期 一 二 三 四 五 六 日 所需售货员人数 18 15 12 16 19 14 12 min 200( ) x1 x2 x3 x4 x5 x6 x7 z = + + + + + + x2 + x3 + x4 + x5 + x6  18 开始休息的人数 x1 x2 x3 x4 x5 x6 x7 设决策变量如上, 建立规划模型如下： x3 + x4 + x5 + x6 + x7  15 x 12 x4 + x5 + x6 + 7 + x1  x 16 x5 + x6 + x7 +x1 + 2  x6 + x7 + x1 + x2 + x3  1914 x7 + x1 + x2 + x3 + x4  x 12 x1 + 2 + x3 + x4 + x5  ,x , , , , , 0 x1 2 x3 x4 x5 x6 x7  x1 ,x2 , x3 , x4 , x5 , x6 , x7 为整数 0.6 5.6 3.6 1.6 1.6 6.6 2.6 0 6 4 2 2 7 3

http://Ixy.xidian.edu.cn/shumo/ 整数线性规对的模型 要求变量取为整数的线性规划问题，称为整数 线性规划问题。如果所有的变量都要求为整数，称 之为纯整数规划或全整数规划；如果仅有一部分变 量要求为整数，则称为混合整数规划 整数线性规划的一般形式（极小化）是： min =CX AX≤(=)b 2ax,≤(eb,i=12,,分 X为整数 i= x为整数j=1,2,…,n (或部分分量为整数

http://lxy.xidian.edu.cn/shumo/ 要求变量取为整数的线性规划问题，称为整数 线性规划问题。如果所有的变量都要求为整数，称 之为纯整数规划或全整数规划；如果仅有一部分变 量要求为整数，则称为混合整数规划。 整数线性规划的模型 整数线性规划的一般形式(极小化)是：            =  = = =   = = x j n a x b i m z c x j n j i j j j n j j j , , , , ( ) , , , , min ,   1 2 1 2 1 1 为整数         = =  ( ) ( ) min 或部分分量为整数 X为整数 AX b z C X T

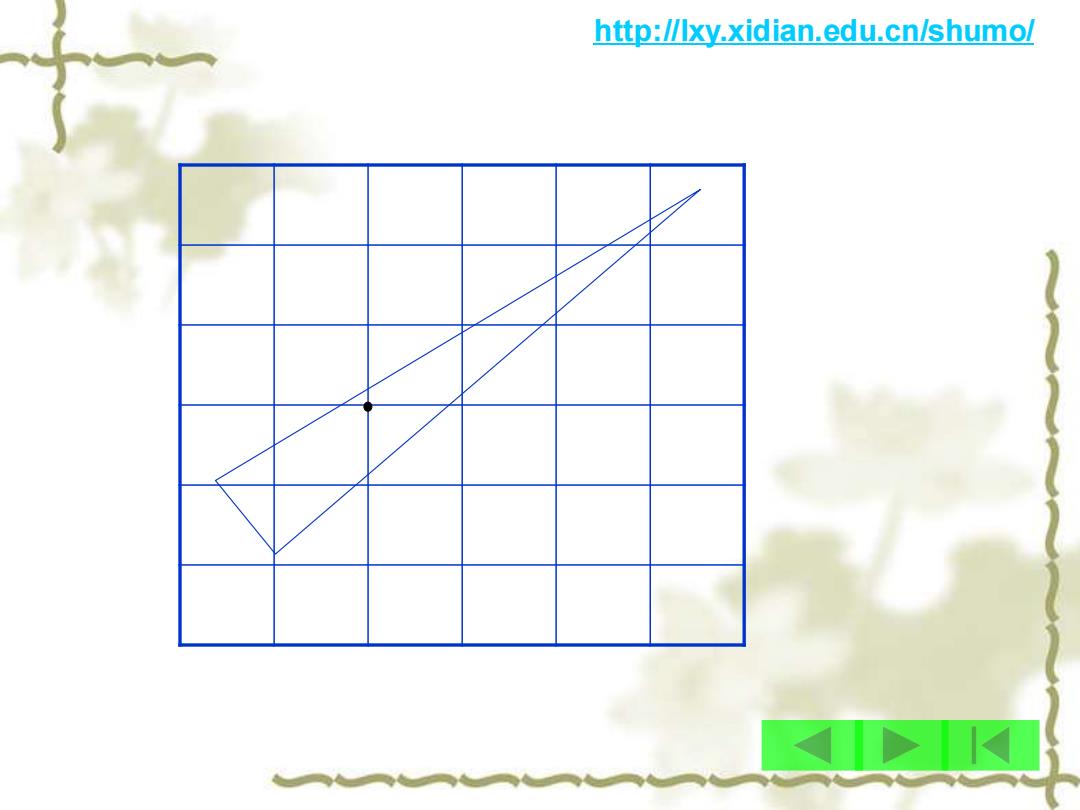
http://Ixy.xidian.edu.cn/shumo/ 举例—图解 max z=20+10 X2 5x+4x2≤24 2x+5x2≤13 2 x,2≥0 五，x2为整数 0 2 3 不考虑整数约束，可得x=4.8,X2=0,目标值96；但 由显然可得最优整数解为x1=4,x2=1,目标值90；

http://lxy.xidian.edu.cn/shumo/ 不考虑整数约束，可得x1=4.8, x2=0,目标值96; 但 由显然可得最优整数解为x1＝4, x2＝1，目标值90； 举例——图解

http://Ixy.xidian.edu.cn/shumo/ 4

http://lxy.xidian.edu.cn/shumo/

http://lxy.xidian.edu.cn/shumo/ 基本求解方法)一分支限界算法 基本思路：先去掉整数约束求解相应的线性规划，若解x 为整数则结束，否则该线性规划的最优值cTx是P问题的上 界U,而P的任一可行解对应一个下界L；进一步将可行域 分枝，逐步减少上界和增大下界，二者相等时终止算法。 min c"x min c"x min c"x s.t.Ax=b s.t.Ax=b s.t.Ax=b →→ x≥0 x≥0 x≥0 x,≥Lx+1 x,sx」 x∈Zm x∈Z axz=40x,+90x2 上界U=356,→(4.81,1.52) S.t.9x1+7x2≤56 下界L=0,→0,0) 7x1+20x2≤70 将原问题分成2个子问题： x1≥0，x2≥0 1)原规划加上≤4； 2)原规划加上x≥5； 1,X2为整数

http://lxy.xidian.edu.cn/shumo/ 基本思路：先去掉整数约束求解相应的线性规划，若解x 0 为整数则结束，否则该线性规划的最优值c Tx 0是IP问题的上 界U，而IP的任一可行解对应一个下界L；进一步将可行域 分枝，逐步减少上界和增大下界，二者相等时终止算法。 max 40x1 90x2 z = + 0, 0 7 20 70 . . 9 7 56 1 2 1 2 1 2   +  +  x x x x s t x x x1 , x2为整数. 上界U＝356，→(4.81,1.52) 下界L＝0，→(0,0) 将原问题分成2个子问题： 1)原规划加上x1≤4； 2)原规划加上x1≥5； 基本求解方法1)——分支限界算法              +  =   n i i T x Z x x x s t Ax b c x 1 0 . . min 0               = x Z x x x s t Ax b c x i i T 0 0 . . min  n T x Z x s t Ax b c x   = 0 . . min

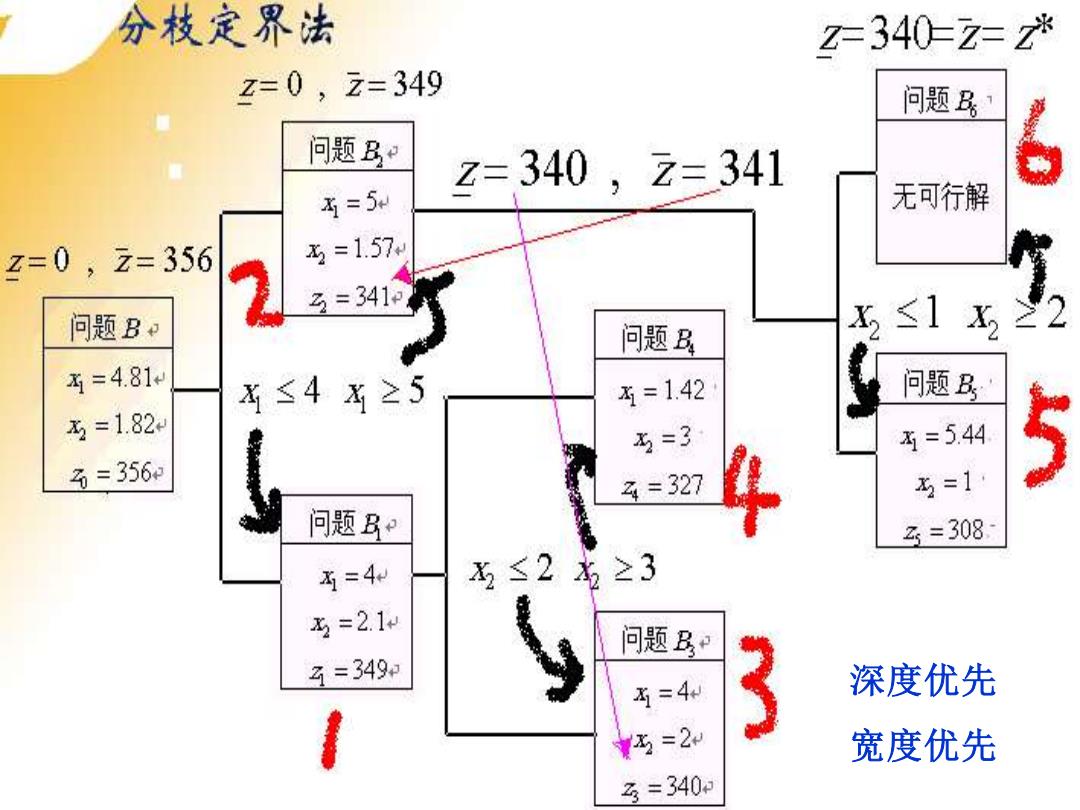
分枝定界法 Z=340-z=z* z=0,z=349 问题B 问题B z=340,z=341 五=5 无可行解 z=0,z=356 五=1.57w 2 3=341P 问题Be 问题B ≤12 5=4.81 ≤4x≥5 五=1.42 问题B x=1.82 五=3 =5.44 石=356 4=327 五=1 问题Be 35=308 五=4 为≤2本≥3 五=2.1 问题B 3=349知 西=4 深度优先 五=2 宽度优先 3=340

http://lxy.xidian.edu.cn/shumo/ 深度优先 宽度优先

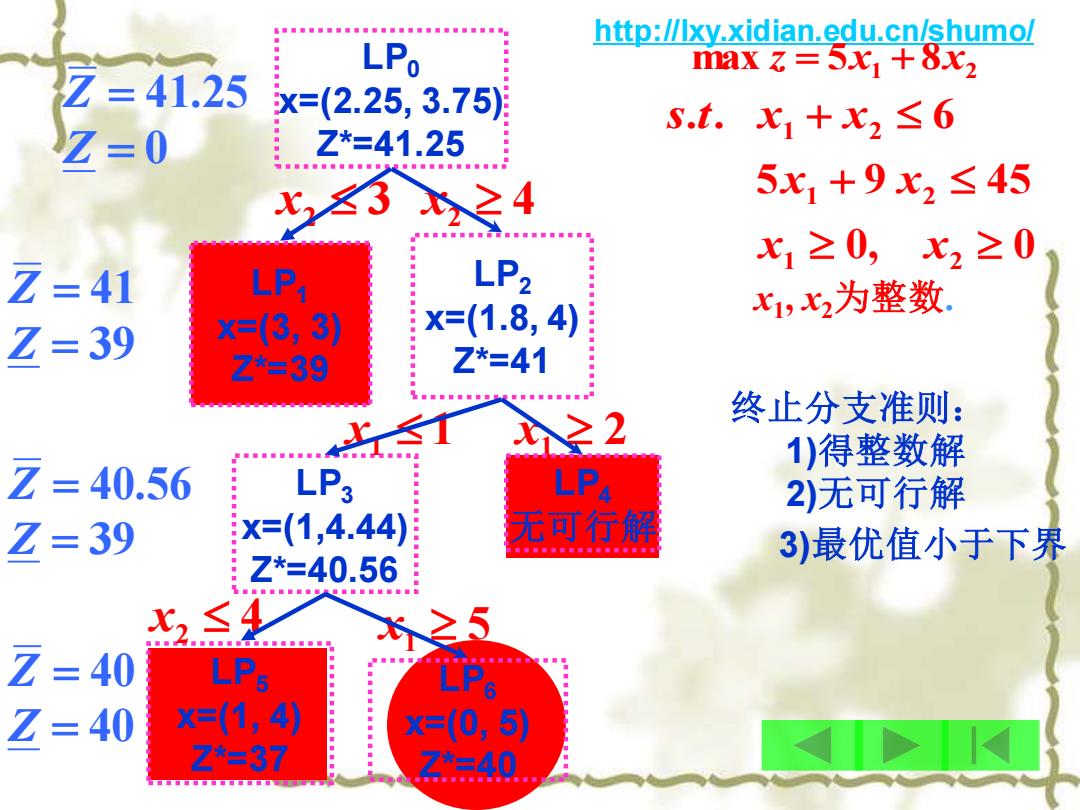
http://lxy.xidian.edu.cn/shumo/ Z=41.25 LPo max=5x+8x2 x=(2.25,3.75) Z=0 Z*=41.25 S.t.x1+x2≤6 x3之4 5x1+9x2≤45 LP2 x1≥0，x2≥0 z=41 LP1 x1,x2为整数. Z=39 x=(3,3) x=(1.8,4) Z*=39 Z*=41 ≥2 终止分支准则： 1)得整数解 Z= 40.56 LP3 LP4 2)无可行解 Z=39 x=(1,4.44)月 无可行解 00日0●■后B00后00B0 3)最优值小于下界 Z*=40.56 X2≤4 Z = LPs Z = 40 X=(1,4) X=(0,5) Z*=37 7*=40

http://lxy.xidian.edu.cn/shumo/ max 5x1 8x2 z = + 0, 0 5 9 45 . . 6 1 2 1 2 1 2   +  +  x x x x s t x x x1 , x2为整数. LP0 x=(2.25, 3.75) Z*=41.25 LP1 x=(3, 3) Z*=39 x2  3 x2  4 LP2 x=(1.8, 4) Z*=41 LP3 x=(1,4.44) Z*=40.56 x1  1 x1  2 LP4 无可行解 LP5 x=(1, 4) Z*=37 x2  4 x1  5 LP6 x=(0, 5) Z*=40 Z = 41.25 Z = 0 Z = 41 Z = 39 Z = 40.56 Z = 39 Z = 40 Z = 40 终止分支准则： 1)得整数解 2)无可行解 3)最优值小于下界

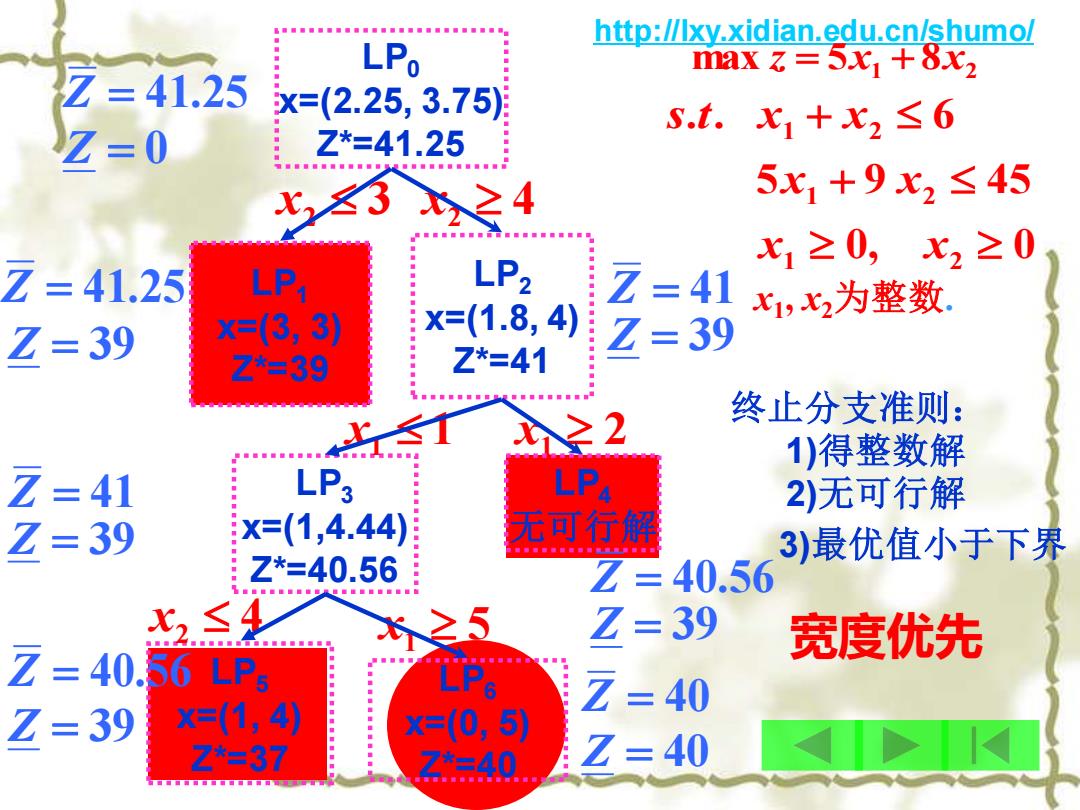
http://lxy.xidian.edu.cn/shumo/ Z=41.25 LPo max=5x+8x2 x=(2.25,3.75) Z=0 Z*=41.25 S.t.x1+x2≤6 x3之4 5x1+9x2≤45 x1≥0，x2≥0 Z=41.25 LP1 LP2 Z=41 x1,x2为整数. Z=39 x=(3,3) x=(1.8,4)月 Z=39 Z*=39 Z*=41 ≥2 终止分支准则： 1)得整数解 z Z == 39 LP3 2)无可行解 x=(1,4.44)月 无可行解 3)最优值小于下界 Z*=40.56 Z = 40.56 X2≤ Z=39 宽度优先 Z LPs 39 40 Z= X=(1,4) X=(0,5) Z*=37 7*=40 Z 40

http://lxy.xidian.edu.cn/shumo/ max 5x1 8x2 z = + 0, 0 5 9 45 . . 6 1 2 1 2 1 2   +  +  x x x x s t x x x1 , x2为整数. LP0 x=(2.25, 3.75) Z*=41.25 LP1 x=(3, 3) Z*=39 x2  3 x2  4 LP2 x=(1.8, 4) Z*=41 LP3 x=(1,4.44) Z*=40.56 x1  1 x1  2 LP4 无可行解 LP5 x=(1, 4) Z*=37 x2  4 x1  5 LP6 x=(0, 5) Z*=40 Z = 41.25 Z = 0 Z = 41.25 Z = 39 Z = 41 Z = 39 Z = 40.56 Z = 39 终止分支准则： 1)得整数解 2)无可行解 3)最优值小于下界 Z = 41 Z = 39 Z = 40.56 Z = 39 Z = 40 Z = 40 宽度优先

http://lxy.xidian.edu.cn/shumo/ Z=41.25 LPo max=5x+8x2 x=(2.25,3.75) Z=0 Z*=41.25 S.t.x1+x2≤6 x34 5x1+9x2≤45 LP2 x1≥0，x2≥0 Z=41.25 Z=41 x1,x2为整数. Z=39 x=(3,3) x=(1.8,4)月 Z=39 Z*=39 Z*=41 ≥2 终止分支准则： 1)得整数解 Z == 9 LP3 LP4 2)无可行解 x=(1,4.44) 无可行解 3)最优值小于下界 Z*=40.56 Z = 40 x2≤4 40 深度优先 NN =9 LPs X=(1,4) 41 ×=(0,5) Z*=37 7*=40 Z 40

http://lxy.xidian.edu.cn/shumo/ max 5x1 8x2 z = + 0, 0 5 9 45 . . 6 1 2 1 2 1 2   +  +  x x x x s t x x x1 , x2为整数. LP0 x=(2.25, 3.75) Z*=41.25 LP1 x=(3, 3) Z*=39 x2  3 x2  4 LP2 x=(1.8, 4) Z*=41 LP3 x=(1,4.44) Z*=40.56 x1  1 x1  2 LP4 无可行解 LP5 x=(1, 4) Z*=37 x2  4 x1  5 LP6 x=(0, 5) Z*=40 Z = 41.25 Z = 0 Z = 41.25 Z = 39 Z = 41 Z = 39 Z = 41 Z = 39 终止分支准则： 1)得整数解 2)无可行解 3)最优值小于下界 Z = 41 Z = 39 Z = 40 Z = 40 Z = 41 Z = 40 深度优先