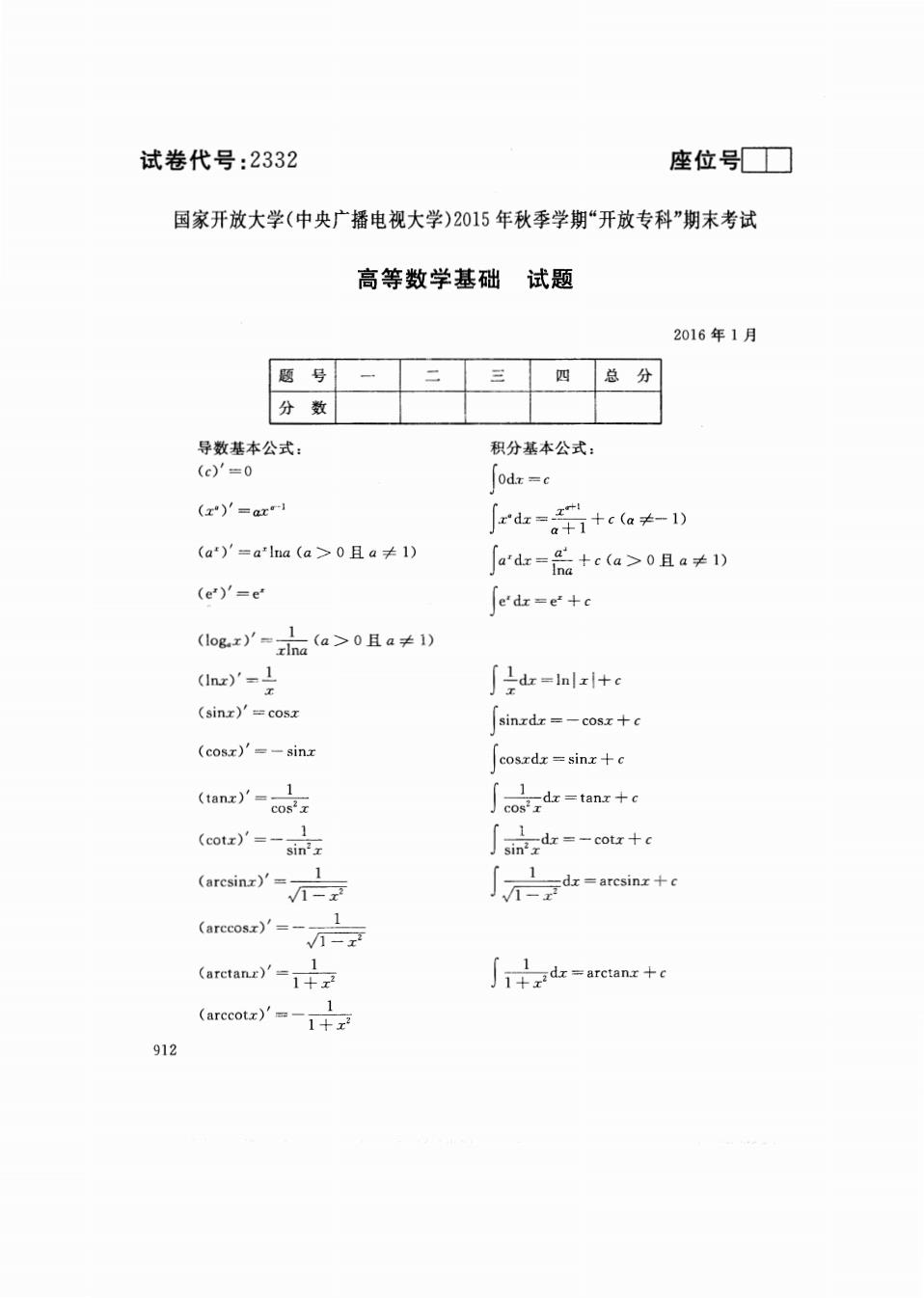
试卷代号:2332 座位号口 国家开放大学(中央广播电视大学)2015年秋季学期“开放专科”期末考试 高等数学基础 试题 2016年1月 题号 三 四 总 分 分数 导数基本公式: 积分基本公式: (c)'=0 0dx=c (z)'=axI r'd= a+7+c(a≠-1) (a)'=a'lna(a>0且a≠1) jard=品+ca>0且a≠1) (e')'=e Je'dr=e+c (1ogx)'=1(a>0且a≠1) xIna (lnx)'= x ∫2=lalz+ (sinz)'=cosx sinxdr=-cosx十c (cosx)'=-sinx cosxdx =sinx+c (tanz)'=-1 s2x ∫od=tar+ (cotx)'=-1 sin'x ∫2d女=-or+c (arcsinz)'=-1 -x _dx =arcsinx+c (arccosz)'=- 1 -x (arctanz)'= 1 1+x 912
试卷代号 :2332 座位号OJ 国家开放大学(中央广播电视大学)2015 年秋季学期"开放专科"期末考试 高等数学基础试题 2016 : j 导数基本公式 (c)' =0 Am?C (x Q )' = ar .,- ~l (a I )' =a"lna (a > 手1) jfd x=-fl 一一十 (u #-一 1) α+1 山=正-卡 (a > 手1) lna (e 巾== X )' = e-' (1 (l 即lX工〉 ,=l_z Csinx)' = cosx (cosx)' = ~- sinx f ! dx =1 中|十 f sinxdx = - cosx f cosxdx = sinx + c (tanz)'=-17 cos- x JJTdz=ta cos- x … (ωz)'=-Jsm~ x j 亘古zdz=-cotzh (aresind=t7 jt7dz= csinx +c (arccoω ,一 主二 Jl-xz -ZI--JU --+-L aa ao nt zz f 1 ~ x2 dx = arct 912

得分评卷人 一、单项选择题(每小题4分,本题共20分) 1.函数曲线y=十二的图形关于( 2 )对称 A.y=z B.x轴 C.y轴 D.坐标原点 2.若函数f(x)= (sin2z, x ,在x=0处连续,则k=(). k, x=0 A.1 B.2 C.-1 n含 3.下列函数在区间(一,十0)上单调诚少的是(). A.cosx B.3-x C.x2 D.2x 4.下列等式成立的是(). A是xd=fe) B.f(r)dz=f(z) C.d f(x)dz=f(x) D.df(z)=f(z) 5.下列无穷限积分收敛的是( 广 nr 得 分 评卷人 二、填空题(每小题4分,共20分) 6.函数y= 9-x n(x-1 、的定义域是 7.函数f(x)= xsin 1 x x<0 的间断点是 x2+1x≥0 8.曲线f(x)=√/x+2在x=2处的切线斜率是 9.函数y=(x十1)2十1的单调减少区间是 10.若f(x)dx=sinx+c,则f(x)= 913
一、单项选择题{每小题 分,本题共 20 分) y …-2 )对称. B. D. 坐标原点 r~旦盐 2. 若函数 fCx) =~工 ,在 x=O 处连续,则是= ( ). !是, .r=O A.1 B.2 c-1D÷ 3. 下列函数在区间(一∞,+∞)上单调减少的是 ). A. cosx B.3-x C.x 2 D.2x 4. 下列等式成立的是 ). A. .~ r fCx)dx = JCx) B. r r Cx)dx = JCx) QXJ J c. dfJ x=J 5. 下列无穷限积分收敛的是( A. ∞叫 c. 2Z dx D.f仙) = JCx) R. 了主dx D. tz 二、填空题(每小题 分,共 20 分) 6. 函数 y=iE J ln(.r 三王-的定义域是 _. 1 ) 函数 fb)=Jzmf I zC) 的间断点是二二- lx .:r二三 8. 曲线 J(.r) ="f~丰言在工 =2 处的切线斜率是 9. 函数 y=C.:r 1)2 的单调减少区间是 10 fJ lnx fω= 913

得分 评卷人 三、计算题(每小题11分,共44分) 11.计算极限im sin3x o sin2x l2.设y=ew+x3,求dy 13.计算不定积分 克. 14.计算定积分 xsinxdx. 得 分 评卷人 四、应用题(本题16分) 15.圆柱体上底的中心到下底的边沿的距离为1,问当底半径与高分别为多少时,圆柱体 的体积最大? 914
们叫 三、计算题(每小题 11 分,共 44 分} 1.计算极限 lim 坐字 .0 S InL;X 12. y=e叩十 dy. 13 计算不定积分 14 计算定积分 xsinxdx 四、应用题{本题 16 分) 15. 圆柱体上底的中心到下底的边沿的距离为/,问当底半径与高分别为多少时,圆柱体 的体积最大? 914

试卷代号:2332 国家开放大学(中央广播电视大学)2015年秋季学期“开放专科”期末考试 高等数学基础试题答案及评分标准 (供参考) 2016年1月 一、单项选择题(每小题4分,本题共20分) 1.C 2.B 3.B 4.A 5.B 二、填空题(每小题4分,本题共20分) 6.(1,2)U(2,3] 7.x=0 8.是 9.(-o,-1) 10.c0s.x 三、计算题(每小题11分,共44分) sin3x lim sin3x 1l.解:lim sin3r=lim3. 3z 3 .63x 3 2 sin2x -2 ……………11分 o sin2x lim sin2r 2 2I 2x 12.解:由微分运算法则和微分基本公式得 dy=d(esinu+')=d(e"in)+d(x) =ed(sin.x)+3x2dx =e"in cosxdx+3x'dx =(ewc0sx+3x2)dx…11分 13.解:由换元积分法得 ∫gdr=-je2d)=-e+c 11分 915
试卷代号 :2332 国家开放大学(中央广播电视大学 )2015 年秋季学期"开放专科"期末考试 高等数学基础 试题答案及评分标准 (供参考) 一、单项选择题{每小题 分,本题共 20 分) l. C 2. B 3. B 4. A 二、填空题{每小题 分,本题共 20 分) 6. (1, 2) U (2 , 3J 7. x=O 8÷ 9. (一∞,一1) 10. cosx 三、计算题(每小题 11 分,共 44 分) -…一 sin3x ,- sin3x 3 3x 3 ~r~~-Õ 3x 3 1.解: lim 豆豆主 =lim 一·一一一=一.二三一一一=一 ;~: • .-õ sin2x ~r-:''-Õ 2 sin2x 2 ,. sin2x 2 一一?一- 11 一-一一 L.- L.- 12. 由微分运算法则和微分基本公式得 dy=d(e'Ül.C +X3) =d( 矿山)十 d(x ) == d(sinx) 3x dx = e"nr cosxdx 3x dx 5. B 2016 -11 = (e cosx + 3x2 ) dx ……………………………………………………………… 11 13. 解:由换元积分法得 jEdz= 归中 =-e +c .11 915

14.解:由分部积分法得 xsinxdx =-xcos +cord 0+sinz =1 …11分 四、应用题(本题16分) 15.解:如图所示,圆柱体高h与底半径r满足 h2+r2= 圆柱体的体积公式为 V=xrh 将2=2一h2代入得 V=x(l-h2)h 求导得 V=π(-2h2+(12-h2)=π(l2-3h2) 令V=0得A-停1,并由此解出=1.即当底半径r-1,高为=时,圆柱体的 3 3 3 体积最大 …16分 916
14. 解:由分部积分法得 二叫工 =-zcOMif+jjc0 = 0 + sin.x I 2 = ………………………………………………………… 11 四、应用题(本题 16 分} 15. 解:如图所示,圆柱体高 与底半径 满足 h2 + r2 = [2 圆柱体的体积公式为 v= h =l2 - 代人得 v= π([2 _ h2)h 求导得 v'= π(- 2h2 + ([2 -h2)) π([2 _ 3h2) v'=o h= .f![, 并由此解出 r= !Ç3 _ . l. 即当底半径 _-. ~ ".~ ,~ r= 3 =,.f! 时,圆柱体的 体积最大. ………........……………………………………………………………………. 16 916