
对偶理

最大最小对偶 目标函数: F(x,y) x∈X,y∈Y x方的目标是无论y怎样,都应使越小越好 y方的目标是无论x怎样,都应使F越大越好; minmax F(x,y) 立于不败之地的决策方法 x∈Xy∈Y 对对偶问题 maxmin F(x,y) 保守主义决策 yeYx∈X 相关结论: 1) minF(x,y)≤F(x,y)≤maxF(x,y),x∈X,y∈Y XEX vEY 2) max min F(x,y)<minmax F(x,y) 一弱对偶定理 yEY xEX x∈XyeY 3) g仰=min max F(x,y)-max min F(x,y)一对偶间隙 x∈XyeY yEY xEX inf 2 min max→ sup
2 最大最小对偶 x X y Y minmax ( , ) F x y F x y x X y Y ( , ) , y Y x X maxmin ( , ) F x y 目标函数: x方的目标是无论y怎样,都应使F越小越好; y方的目标是无论x怎样,都应使F越大越好; 立于不败之地的决策方法 ——保守主义决策 相关结论: ——一对对偶问题 x X y Y 1) min ( , ) ( , ) max ( , ), , F x y F x y F x y x X y Y y Y y Y x X x X 2) maxmin ( , ) minmax ( , ) F x y F x y ——弱对偶定理 x X x X y Y y Y 3) minmax ( , ) maxmin ( , ) gap F x y F x y = − ——对偶间隙 min max inf sup

最大最小对偶举例一博弈 x∈X={1,2},y∈Y={1,2,F(x,y)=ag, 4a,)[日 min max F(x,y)=2 xEX yEY 8p=0 max min F(x,y)=2 yeYx∈X =,[日到 min max F(x,y)=2 x∈XyeY 8吧=1≠0 max min F(x,y)=1 vEY xEX 3
3 最大最小对偶举例——博弈 x X y Y minmax ( , ) 2 F x y = x X y Y = = 1,2 , 1,2 , y Y x X maxmin ( , ) 2 F x y = F x y axy ( , ) , = A aij 1 2 ( ) 4 3 − = = gap = 0 A aij 1 2 ( ) 4 1 − = = x X y Y minmax ( , ) 2 F x y = y Y x X maxmin ( , ) 1 F x y = gap = 1 0

最大最小对偶 鞍点条件:对 F(x,y),x∈X,y∈Y,若有点x∈X,y∈Y F(x,y)≤F(x,y)≤F(x,Jy),x∈X,y∈Y 则称(x*y*)满足鞍点条件。 相关结论: 1) minF(x,y)≤F(x,y)≤maxF(x,y),x∈X,y∈Y XEX yey 2) max min F(x,y)≤min max F(x,y)一弱对偶定理 yEY xEX xEx yEY 3) gap minmax F(x,y)-max min F(x,y) x∈XyeY yEY xEX 一对偶间隙 4) minmax F(x,y)=max min F(x,y) xEX yEY yEY xEX 台(x,y)满足鞍点条件。 强对偶定理 4
4 最大最小对偶 鞍点条件: 对 F x y x X y Y ( , ), , , 相关结论: x X y Y 1) min ( , ) ( , ) max ( , ), , F x y F x y F x y x X y Y y Y y Y x X x X 2) maxmin ( , ) minmax ( , ) F x y F x y ——弱对偶定理 x X x X y Y y Y 3) minmax ( , ) maxmin ( , ) gap F x y F x y = − ——对偶间隙 若有点 * * x X y Y , F x y F x y F x y x X y Y * * * * ( , ) ( , ) ( , ), , 则称(x*,y*)满足鞍点条件。 x X x X y Y y Y 4) minmax ( , ) maxmin ( , ) F x y F x y = ——强对偶定理 x y * * ( , ) 满足鞍点条件

Lagrange对偶 min f(x) 原规划: s.t.gxy≤0,h(x)=0 Lagrange函数 L(x,u,v)=f(x)+u'g(x)+vh(x) (u≥0) Lagrange对偶 maxθ(u,y) 凹函数 ≥0,y 其中i)=mi{f)+ug()+vx},u≥0 弱对偶性: 1) x∈S,w≥0,y, f(x),x∈S minL(x,4,y)≤L(x,u,y)=f(x)≤maxL(x,u,y)= x∈R" 20,y +o0,x庄S 2) max min L(x,w,)=max(u,)≤min max L(x,D弱对偶定理 u20,v xER" l≥0,y XER,v 原规划 min max L(x,u,v)-max min L(x,u,v) x∈R"20,y ≥0,yx∈R" 一对偶间隙 5
5 f x s t g(x) h x min ( ) . . 0, ( ) 0 = 原规划: Lagrange对偶 T T Lagrange函数 L x u v f x u g x v h x u ( , , ) ( ) ( ) ( ) ( 0) = + + Lagrange对偶 n T T x R ( , ) min ( ) ( ) ( ) , 0 u v f x u g x v h x u 其中 = + + 弱对偶性: n n u v u v u v x R x R L x u v u v L x u v 0, 0, 0, 2) maxmin ( , , ) max ( , ) minmax ( , , ) = n x R u v f x x S L x u v L x u v f x L x u v 0 , x S ( ), min ( , , ) ( , , ) ( ) max ( , , ) , = = + 1) , 0, , x S u v n n x R x R u v u v L x u v L x u v 0, 0, 3) minmax ( , , ) maxmin ( , , ) − ——弱对偶定理 ——对偶间隙 原规划 u v u v 0, max ( , ) 凹函数

Lagrange对偶举例 min max L(x,u,v)-max min L(x,u,v) x∈R"20,y u20,v xER" min x2 min 2 x∈0,2] s.t.1-x≤0 S.t.1-x=0 min x好+x号 minx好+x好 S.t.4-x1-X2≤0 S.t.4-X1-2=0 1,x2≥0 七1,x2≥0 mi 1-2x1+2 S.t.3-X1-x2=0 (x1,x2)∈{(0,0),(0,4),(4,4),(4,0),(1,2),(2,1)} 6
6 x s t x 2 min . . 1 0 − Lagrange对偶举例 2 [0,2] min . . 1 0 x x s t x − − = n n x R x R u v u v L x u v L x u v 0, 0, minmax ( , , ) maxmin ( , , ) − x x s t x x x x 2 2 1 2 1 2 1 2 min . . 4 0 , 0 + − − x x s t x x x x 1 2 1 2 1 2 min -2 . . 3 0 ( , ) (0,0),(0,4),(4,4),(4,0),(1, 2),(2,1) + − − = 2 2 1 2 1 2 1 2 min . . 4 0 , 0 x x s t x x x x + − − =
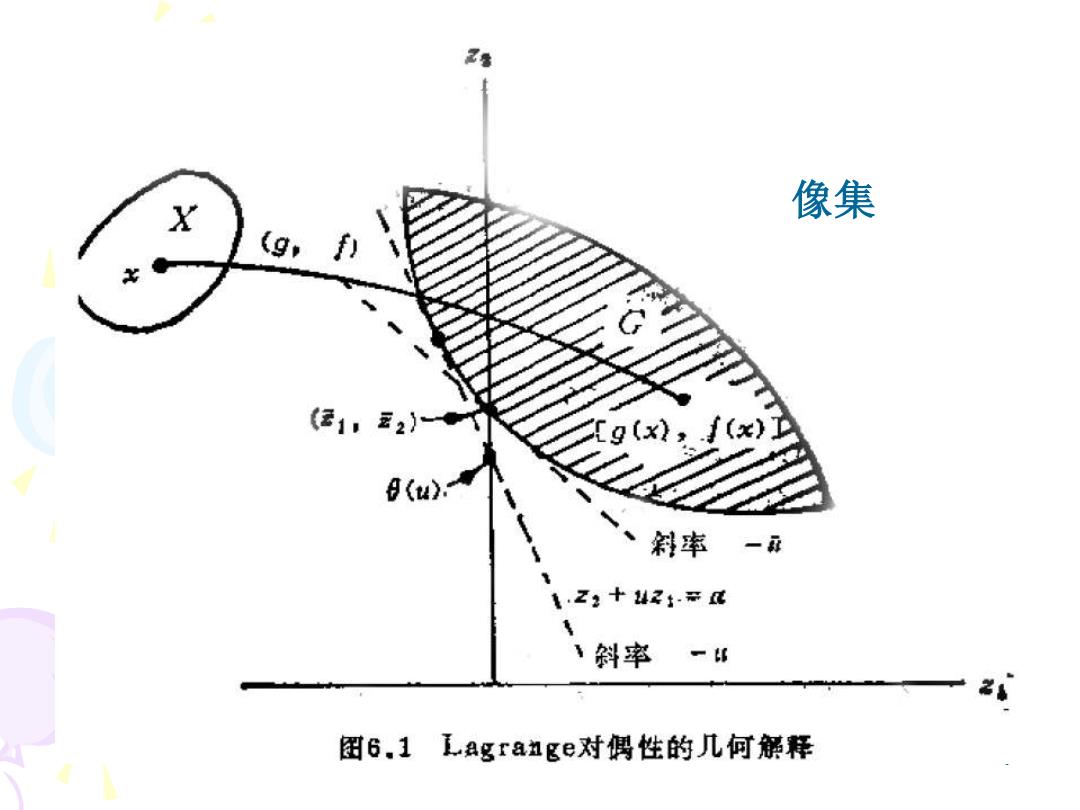
乙堡 X 像集 (g,f) (运1,玉2) (x)D (u. 斜率一麻 122+42:=d 、斜率 -i 图6.1 Lagra边ge对偶性的几何解释
7 像集
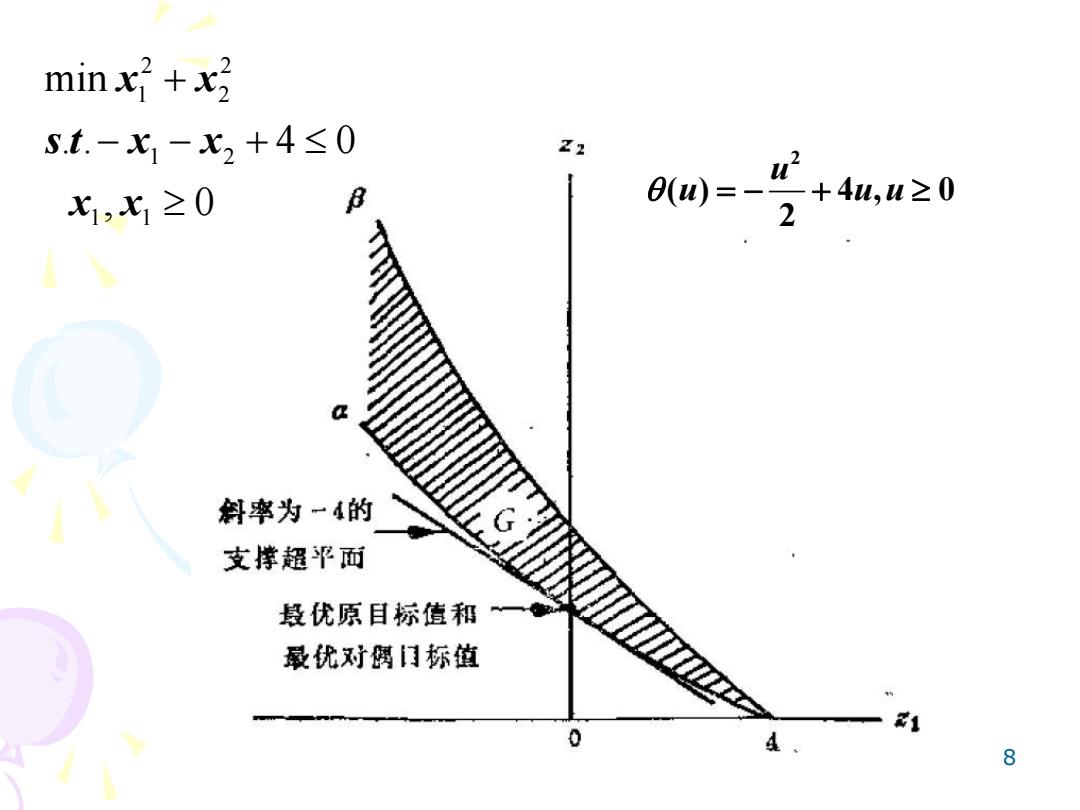
minx2+x号 S.t.-x1-x2+4≤0 Z2 X1,x1≥0 ®C=-+4u,w≥0 斜率为一4的 支撑超平而 最优原目标值和 最优对俩日标值 1 0 4、 8
8 2 2 1 2 1 2 1 1 min . . 4 0 , 0 x x s t x x x x + − − + 2 ( ) 4 , 0 2 u u u u = − +
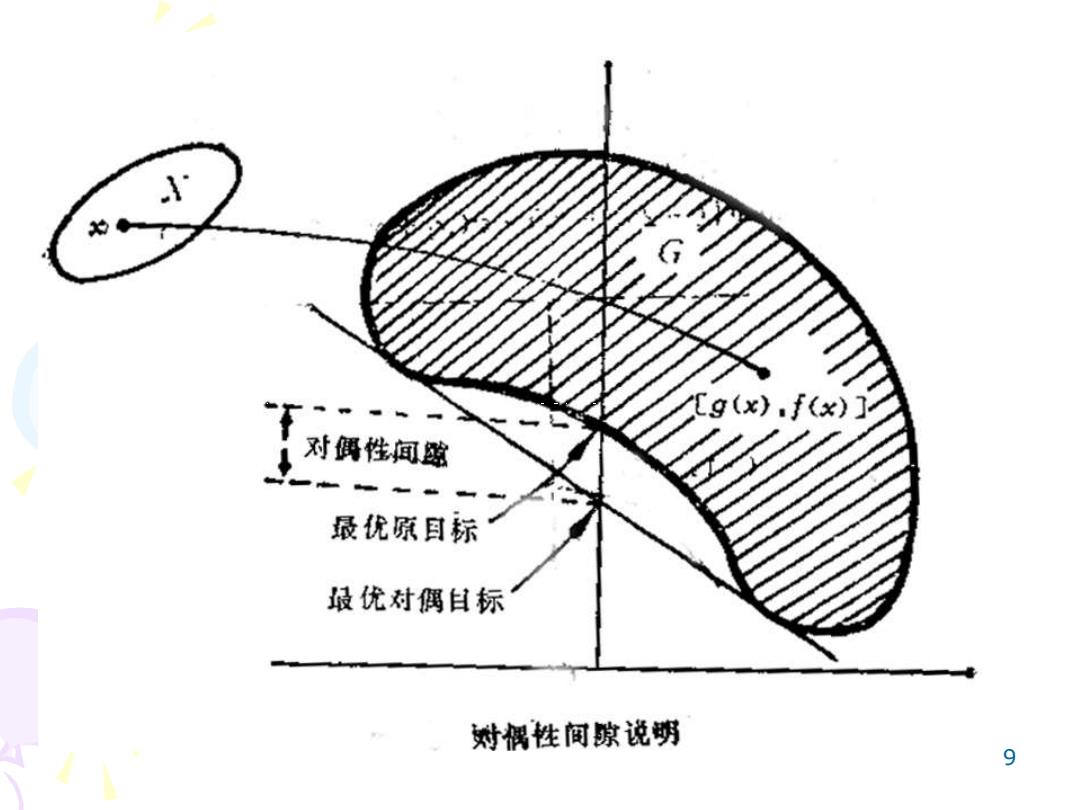
[g(x).f(x) 对偶性闻噬 最优原耳标 最优对偶目标 射偶性间隙说明 9
9

Lagrange对偶的强对偶定理 min f(x) 连续可微凸规划: s五.gy≤0,h(x)=0不8可微凸,h线性 强对偶定理:连续可微凸规划,满足一约束规格,则 1):若原问题有解,则对偶问题也有解; 2):若原问题与对偶问题分别有可行解,则他们是最优解的充分 必要条件是他们对应相同的目标值(对偶间隙为0). 3):对偶问题无上界,则原问题不可行;原问题无下界,则对偶 问题不可行。 证1):即证可微凸规划的最优解x与其KKT条件的乘子(u,) 满足鞍点条件! 证2):利用鞍点条件可得。 参阅《Nonlinear Programming-Theory and Algorithm》第6章 M.S.Bazaraa&C.M.Shetty(图书馆有中译本) 10
10 f x s t g(x) h x min ( ) . . 0, ( ) 0 = 连续可微凸规划: 强对偶定理:连续可微凸规划,满足一约束规格,则 Lagrange对偶的强对偶定理 f、g可微凸,h线性 1):若原问题有解,则对偶问题也有解; 2):若原问题与对偶问题分别有可行解,则他们是最优解的充分 必要条件是他们对应相同的目标值(对偶间隙为0). 证1):即证可微凸规划的最优解 x 与其KKT条件的乘子 (u v, ) 满足鞍点条件! 证2):利用鞍点条件可得。 参阅《Nonlinear Programming-Theory and Algorithm》第6章 M. S. Bazaraa & C. M. Shetty(图书馆有中译本) 3):对偶问题无上界,则原问题不可行;原问题无下界,则对偶 问题不可行