
数学建模讲义 建模慨论与初等模型
数学建模讲义 建模概论与初等模型
数学建模概论 什么是数学模型 玩具、照片 实物模型 我们常见 风洞中的飞机. 物理模型 的模型 地图、电路图… 符号模型 模型是为了一定目的,对客观事物的一部分进行 简缩、抽象、提炼出来的原型的替代物。 模型集中反映了原型中人们需要的那一都分特征
风洞中的飞机… ——物理模型 地图、电路图… ——符号模型 模型是为了一定目的,对客观事物的一部分进行 简缩、抽象、提炼出来的原型的替代物。 模型集中反映了原型中人们需要的那一部分特征. 我们常见 的模型 什么是数学模型 一、数学建模概论 玩具、照片…… ——实物模型

数学模型 (Mathematical Model) 数学建模 (Mathematical Modeling) 数学模型—一对于一个现实对象,为了一个特定目的 根据其内规律,作出必要的简化假设,运用适当的数 学工具,得到的一个数学结构 数量关系 数学建模一是利用数学方法解决实际问题的一种 实践过程.即通过抽象、简化、假设、引进变量等处 理过程后,将实际问题用数学方式表达,以建立起数 学模型,然后运用先进的数学方法及计算机技术进行 求解. 数学建模指建立数学模型的全过程。 包括模型建立、求解、分析、检验。 观点:“所谓高科技就是一种数学技术
数学模型 (Mathematical Model) 数学建模(Mathematical Modeling) 数学建模指建立数学模型的全过程。 ——包括模型建立、求解、分析、检验。 数学模型——对于一个现实对象,为了一个特定目的, 根据其内规律,作出必要的简化假设,运用适当的数 学工具,得到的一个数学结构。 数学建模——是利用数学方法解决实际问题的一种 实践过程. 即通过抽象、简化、假设、引进变量等处 理过程后, 将实际问题用数学方式表达,以建立起数 学模型, 然后运用先进的数学方法及计算机技术进行 求解. 观点:“所谓高科技就是一种数学技术” 数量关系

R+r 数学建模三大功能一解释,判断,预见 1.解释 孟德尔遗传定律的“3:1” Rr(xRr) 2.判断 放射性废物处理 RRRr rR 美国原子能委 员会提出如下处理 3预见 谷神星的发现 浓缩放射性废物 : 阻 0.08y 封装入密封性很好 浮 行星的轨R=0×+3x2四) 的坚固的桶中 道半径 沉入300f的海里 n=-10,0,1,2,?,4,5 而一些工程师提出 水、金、地、火、木、土 质疑?需要判断方 案的合理性。 1781年,利用这个结果发现了天王 星,1802年,发现了谷神星与3对 重 V30o940t/s 应(有故事),之后还发现了海王星、 冥王星
1. 解释——孟德尔遗传定律的“3:1” 数学建模三大功能——解释, 判断, 预见 美 国原 子能委 员会提出如下处理 浓缩放射性废物: 封装入密封性很好 的坚固的圆桶中, 沉入300ft的海里, 而一些工程师提出 质疑?需要判断方 案的合理性。 2.判断——放射性废物处理 R + r Rr (Rr) RR Rr rR rr 3.预见——谷神星的发现 ( ) n R 4 3 2 10 1 行星的轨 = + 道半径 n = −10,0,1,2,?,4,5 水、金、地、火、木、土 1781年, 利用这个结果发现了天王 星, 1802年,发现了谷神星与3对 应(有故事),之后还发现了海王星、 冥王星。 F浮 f 阻 = 0.08v F重 v 40 ft / s 300 ?

你碰到过的数学模型 航行问题 甲乙两地相距750公里,船从甲到乙顺水航行 需30小时,从乙到甲逆水航行需50小时,问船的速 度是多少? 用x表示船速,y表示水速,列出方程: (x+y)×30=750 (x一y)×50=750 求解得到x=20,y=5,答:船速每小时20公里
你碰到过的数学模型——航行问题 用x表示船速,y表示水速,列出方程: ( ) 50 750 ( ) 30 750 − = + = x y x y 求解得到 x=20, y=5,答:船速每小时20公里. 甲乙两地相距750公里,船从甲到乙顺水航行 需30小时,从乙到甲逆水航行需50小时,问船的速 度是多少?

航行问题建立数学模型的基本步骤 作出简化假设(船速、水速为常数,方向一致); 用符号表示有关量化,y表示船速和水速); ·用物理定律(匀速运动的距离等于速度乘以 时间)列出数学式子(二元一次方程); 求解得到数学解答(x=20,y=5); 回答原问题(船速每小时20公里)
航行问题建立数学模型的基本步骤 • 作出简化假设(船速、水速为常数, 方向一致); • 用符号表示有关量(x, y表示船速和水速); • 用物理定律(匀速运动的距离等于速度乘以 时间)列出数学式子(二元一次方程); • 求解得到数学解答(x=20, y=5); • 回答原问题(船速每小时20公里)

录象机计数器的用途 经试验,一盘录像带从头走到尾, 时间用了183分30秒,计数器读数从 0000变到6152。在一次使用中录像带已 题 经转过大半,计数器读数为4580,问剩 下的一段还能否录下1小时的节目? 聚 不仅仅回答问题,而且建立计数器读数与 绿像带转过时间的关系 个数学模型 日常问题:常见的录音机的转轴转动是匀速的吗? 思考 本题中计数器读数是均匀增长的吗?
录象机计数器的用途 问 题 经试验,一盘录像带从头走到尾, 时间用了183分30秒,计数器读数从 0000变到6152。在一次使用中录像带已 经转过大半,计数器读数为4580,问剩 下的一段还能否录下1小时的节目? 要 求 不仅仅回答问题, 而且建立计数器读数与 录像带转过时间的关系——一个数学模型! 思考 本题中计数器读数是均匀增长的吗? 日常问题:常见的录音机的转轴转动是匀速的吗?

等 万 000 的 4
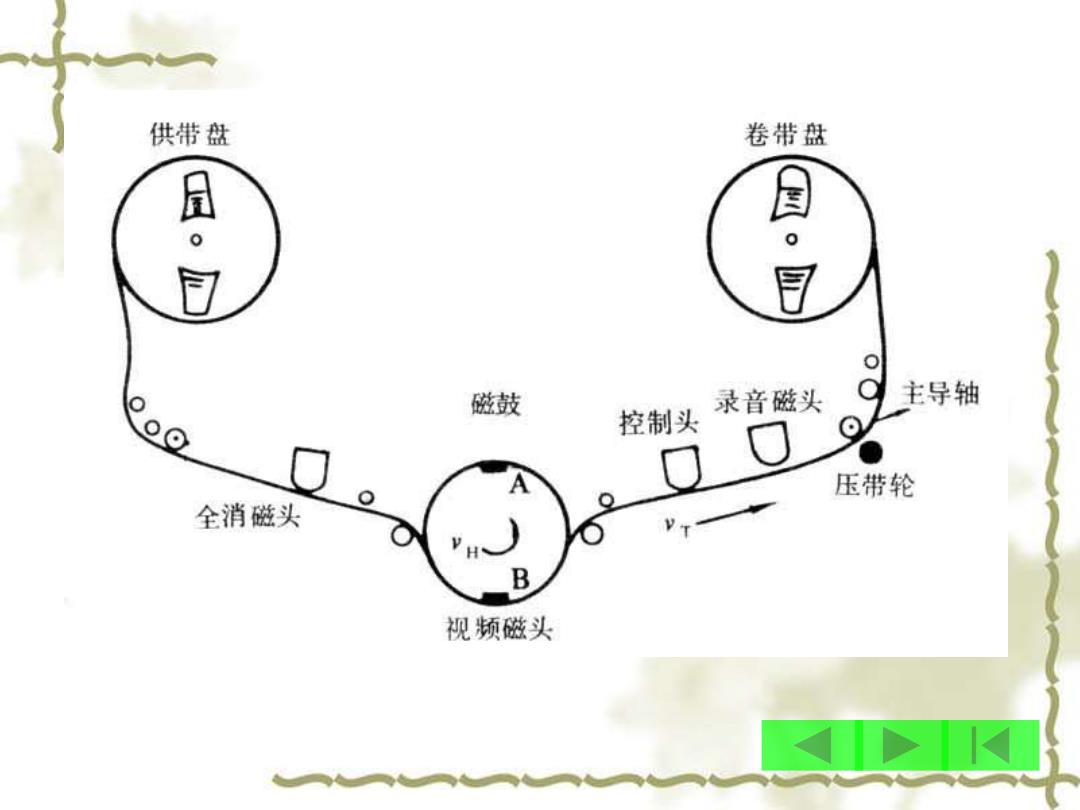
供带盘 卷带盘 员 0 0 包 磁鼓 录音磁头 主导轴 控制头 压带轮 全消磁头 B 视频磁头
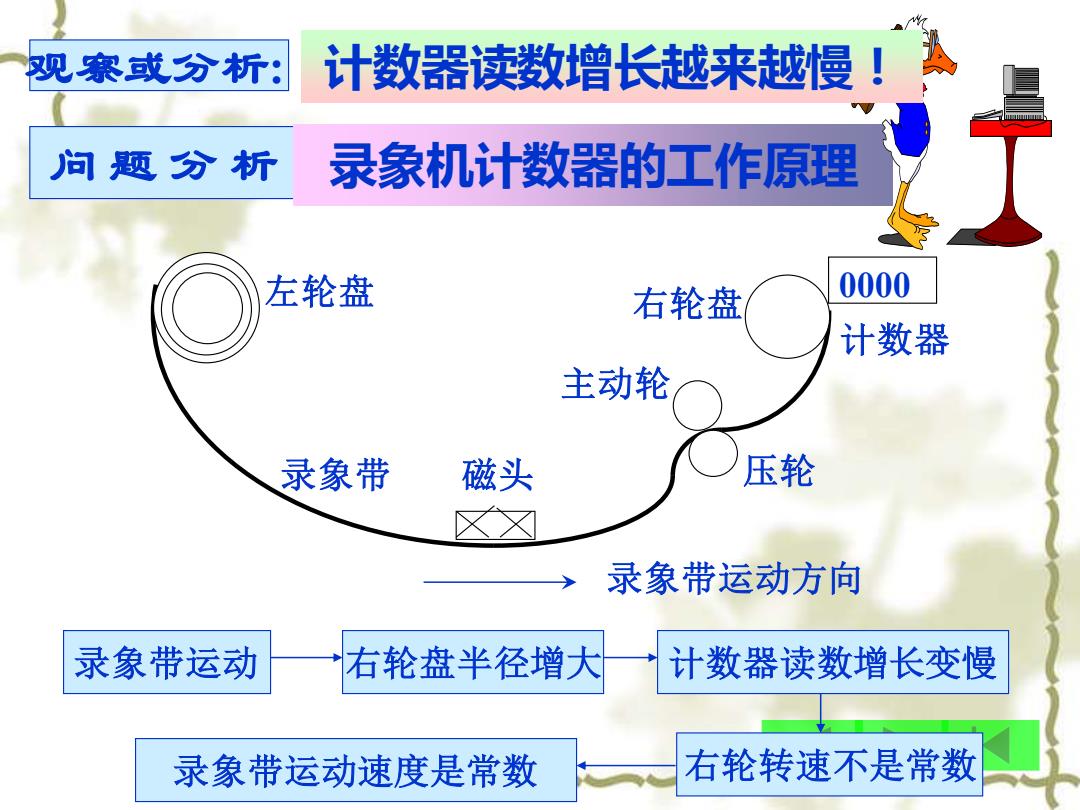
观察或分析: 计数器读数增长越来越慢! 问题分析 录象机计数器的工作原理 左轮盘 右轮盘 0000 计数器 主动轮 录象带 磁头 压轮 录象带运动方向 录象带运动 右轮盘半径增大 计数器读数增长变慢 录象带运动速度是常数 右轮转速不是常数
问 题 分 析 录象机计数器的工作原理 左轮盘 0000 右轮盘 磁头 主动轮 压轮 计数器 录象带 录象带运动方向 录象带运动 右轮盘半径增大 录象带运动速度是常数 右轮转速不是常数 计数器读数增长变慢 观察或分析: 计数器读数增长越来越慢!