西安电子科技大学：《工程优化方法》课程教学资源（PPT课件讲稿）约束优化（非线性规划理论与算法）

非线性规划理论与算法 ·非线性规划及其最优性条件 ·对偶理论 ·外点罚函数法 ·内点罚函数法 1

1 非线性规划理论与算法 • 非线性规划及其最优性条件 • 对偶理论 • 外点罚函数法 • 内点罚函数法

非线性规划 设x=(x1,,xn)I∈R”,f(x),C,(x):R”→R,i=1,2,,p+q,如下约束问 题称为非线性规划(Nonlinear Programming,NP): min f(x) min f(x) p=q=0即无约束规划 s.t.c,(x)≤0，i=1,,p x∈S c,(x)=0,i=p+1,,p+q 约束集或可行域：S={x∈R”c,(x)≤0，i=1,p,c,(x)=0,j=p+1,,p+q} x*是整体（全局）极小点台∈S,f(x)≥f(x*) x*是严格整体（全局）极小点台Vx∈S\{x,f(x)>f(x*) x*是局部极小点÷x∈Sn{x∈R”lx-x*f(*) 非线性规划向量化表示 令g(x)=(c(x,cn(x)》, min f(x) s.t. gy≤0 x)=(cp+1(x,cp+p(x》 3 h(x)=0

3 设 T n x = (x1 ,..., xn )  R ， ( ), ( ) : n i f x c x R R , i p q = + 1,2, , ，如下约束问 题称为非线性规划(Nonlinear Programming, NP)： min ( ) . . ( ) 0, 1,..., ( ) 0, 1,..., i i f x s t c x i p c x i p p q     =  = = + +   ( ) 0, 1,..., , ( ) 0, 1,...,  n 约束集或可行域: S x R c x i p c x j p p q =   = = = + + i i 非线性规划 x*是整体(全局)极小点     x S f x f x , ( ) ( *) x*是严格整体(全局)极小点     x S x f x f x \ { }, ( ) ( *) x*是局部极小点  * , ( ) ( *)  n     −   x S x R x x f x f x  x*是严格局部极小点  * , ( ) ( *)  n     −   x S x R x x f x f x  min ( ) x S f x  1 1 ( ) ( ( ),..., ( )) , ( ) ( ( ),..., ( )) T p T p p p g x c x c x h x c x c x + + = = 令 min ( ) . . 0 ( ) 0 f x s t g(x) h x       = 非线性规划向量化表示 p=q=0即无约束规划

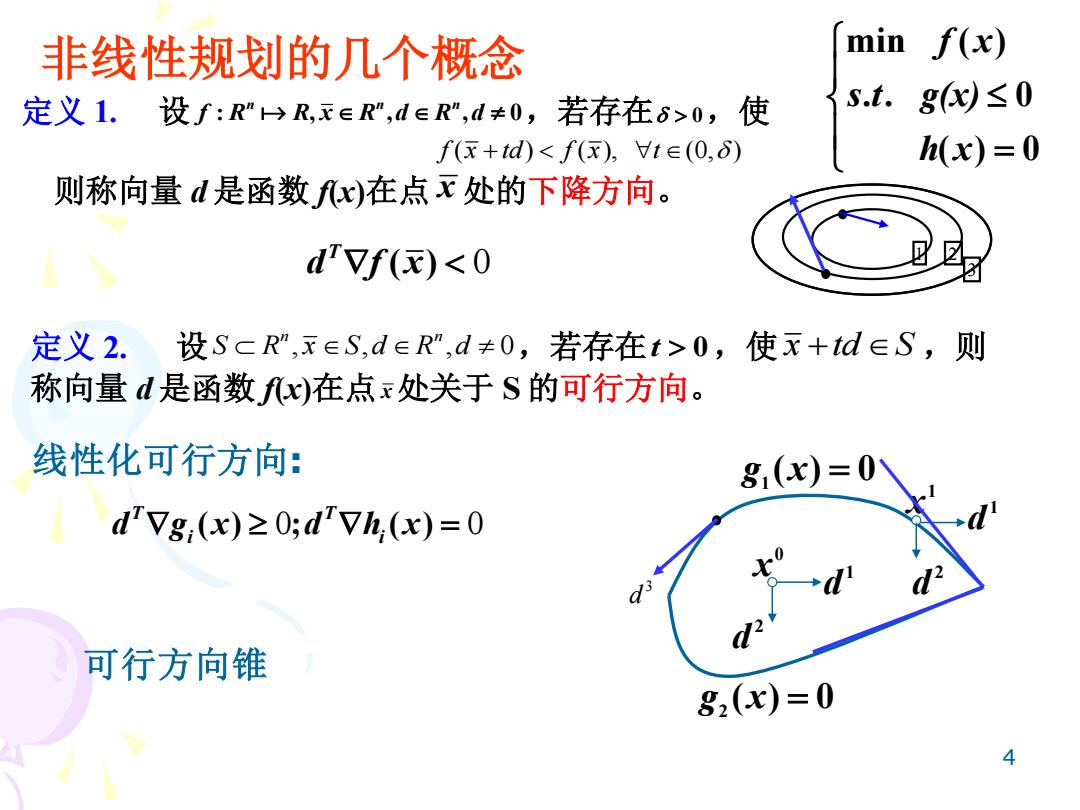
非线性规划的几个概念 min f(x) 定义1.设f:R"→R,x∈R",d∈R",d≠0，若存在6>0，使 s.t.gx≤0 f(x+td)0,使x+td∈S,则 称向量d是函数fx)在点x处关于S的可行方向。 线性化可行方向： 81(x)=0\ dVg,(x)≥0；drVh,(x)=0 可行方向锥 82(x)=0 4

4 非线性规划的几个概念 定义 1. 设 : , , , 0 n n n f R R x R d R d    ，若存在  0，使 f x td f x t ( ) ( ), (0, ) +     则称向量 d 是函数 f(x)在点 x 处的下降方向。 定义 2. 设 , , , 0 n n S R x S d R d     ，若存在t  0，使 x td S +  ，则 称向量 d 是函数 f(x)在点x处关于 S 的可行方向。 线性化可行方向: ( ) 0 T d f x   ( ) ; ( ) 0 0 T T i i d g x d h x    = min ( ) . . 0 ( ) 0 f x s t g(x) h x       = g1 (x) = 0 g2 (x) = 0 0 x 1 x 1 d 1 d 2 d 2 d 1 2 3 3 d 可行方向锥

min f(x) s.t.g≤0 定义3：积极约束： h(x)=0 设点x∈Q,对于不等式约束g,(x)≤0，如果g()=0, 则称g,(x)≤0是点x处的积极约束。 或起作用约束（紧约束积极约束八有效约束) 。 记1()={ig,()=0,1≤i≤)，称I()为点x处的积极约束指标集。 例：设g(x)=V2x2-x2≤0,8()=x2+x号-1≤0,8，()=-x≤0. 令x=(5,5y,则)=，24 2’2 x2 g2(x)=0 g1(x)=0 83(x)=0 5

5 定义3: 积极约束: , ( ) 0 ( ) 0, ( ) 0 i i i x Q g x g x g x x   =  设点 对于不等式约束 ，如果 则称 是点 处的积极约束。 或起作用约束（紧约束\积极约束\有效约束）。 ( ) { | ( ) 0,1 }, ( ) i 记I x i g x i l I x x = =   称 为点 处的积极约束指标集。 2 2 2 1 1 2 2 1 2 3 1 ( ) 2 0, ( ) 1 0, ( ) 0 2 2 ( , ) ( ) 2 2 T g x x x g x x x g x x x I x = −  = + −  = −  = = 例：设 . 令 ，则 {1,2}. 1 x 2 x O g2 (x) = 0 g1 (x) = 0 g3 (x) = 0 x min ( ) . . 0 ( ) 0 f x s t g(x) h x       =

min f(x) 定理1： s.t.g(x≤0 给定点x∈Q,记点x的积极约束指标集为 I(x)。给定向量d, 如果对任意的i∈I(x)有Vg:(x)'d0。则对任意的i∈I(x),有 8(x')=g:(x)+t7gx)'d+o(td2) =tVg;(x)'d+o(ltd)<0 ∴.x'∈Q,即d为可行方向。 定义4：可行下降方向 设点x∈O,给定向量d,如果d既是点x处的可行方向， 又是该点的下降方向， 则称d为点x处的可行下降方向：

6 令 x'= x + t d ,t  0。则对任意的i  I(x),有 ( ') ( ) ( ) (|| || ) 2 g x g x t g x d o td T i = i +  i + ( ) (|| || ) 2 t g x d o td T =  i +  0  x'Q,即d为可行方向。 又是该点的下降方向，则称 为点 处的可行下降方向。 设点 ，给定向量 ，如果 既是点 处的可行方向， d x x Q d d x 证明: 定理1: 定义4: 可行下降方向 如果对任意的 有 则 是 点 的可行方向。 给定点 记 点 的积极约束指标集为 。给定向量 ， i I x g x d d x x Q x I x d T i ( ) ( ) 0, , ( )     min ( ) . . 0 f x s t g(x)    

定理2： min f(x) 给定点x∈2，记点x的积极约束指标集为(x)。给定(S.t.g)≤0 向量d,如果d满足 7g,(x)'d<0i∈1x) Vf(x)'d<o 则向量d是点x处的可行下降方向。 证略 ③极值点的必要条件： 定理3： 设x*∈Q,I(*)是其积极约束指标集。 f(x)和gi(x)(i∈I(x*)在点x*处可微， g(x)(i庄I(x*)在点x*处连续。 如果x*是约束极值问题)的局部极小点，则在 点x*处没有可行下降方向。 7

7 则向量 是 点 处的可行下降方向。 向 量 ，如果 满 足 给定点 记 点 的积极约束指标集为 。给定 d x f x d g x d i I x d d x Q x I x T T i          ( ) 0 ( ) 0 ( ) , ( ) 设 x*Q，I(x*)是其积极约束指标集。 定理2: 定理3: 证略 ③极值点的必要条件: f (x)和gi (x)(i  I(x*))在点x*处可微， gi (x)(i  I(x*))在点x*处连续。 点 处没有可行下降方向。 如 果 是约束极值问题 的局部极小点，则在 * * (1) x x min ( ) . . 0 f x s t g(x)    

定义5. 设ScR",称S为凸集当且仅当x1,x2∈S及V1∈0，山都有 2x1+(1-2)x2∈S 定义6. 设x,,,xne”,称x是xx2…,x,的一个凸组合当且仅当存在 ∑=1,20使x=1。 定义7.设S∈R”,称f是S上的凸函数当且仅当对x,x2∈S及 H∈0，川都有 f(2x1+(1-兄)x2)≤元fx1)+(1-)f(x2) 严格凸组合 严格凸 线性组合 定理若fx)是S上的凸函数，则ceR,水平集X={xESf(,x)≤c是凸集 若是凸函数，S是凸集，inf(X)为凸规划。凸规划的局部解是整体解！ x∈S S={x∈R”lc,()≤0，i=1,P,c(x)=0,j=p+1,p+4 般要求C,(x)当=1,2，.…p时为凸函数，当p叶1，…p叶g时为线性函数。 8

8 定义 5. 设 n S R  ，称 S 为凸集当且仅当 1 2   x x S , 及  [0,1]都有 1 2   x x S + −  (1 ) 定义 6. 设 1 2 , , , n p x x x R  ，称 x是 1 2 , , , p x x x 的一个凸组合当且仅当存在 1 1, 0 l i i i   =  =  使 1 l i i i x x  = =  。 定义 7. 设 n S R  ，称 f 是 S 上的凸函数当且仅当对 1 2   x x S , 及   [0,1]都有 1 2 1 2 f x x f x f x ( (1 ) ) ( ) (1 ) ( )     + −  + − 严格凸组合 严格凸 线性组合 定理 若 f(x)是 S 上的凸函数，则 c R，水平集 X x S f x c =    ( ) 是凸集. min ( ) x S f x  若f(x)是凸函数，S是凸集， 为凸规划。  ( ) 0, 1,..., , ( ) 0, 1,...,  n S x R c x i p c x j p p q =   = = = + + i i 一般要求 ( ) i c x 当i=1,2,…,p时为凸函数，当i=p+1,…,p+q时为线性函数。 凸规划的局部解是整体解！

af(x) a'f(x) a2f(x) @'f(x) 0x1 Ex? x 8x2 xx af(x) a'f(x) 8'f(x) 82f(x) ax ox x xox Vf(x)= 0x2 V2f(x)= af(x) a2f(x) a'f(x) a"f(x) axm」 ox ox ax ox2 x 定理（凸函数的一阶充要条件） 若fx)在S上可微，则fx)是凸函 数当且仅当 f(x)≥f()+Vf)'(x-),E∈S 定理（凸函数的二阶充要条件）设∫：S→R二阶连续可导，则 1)f是S上的凸函数的充要条件是f的Hesse矩阵Vf(x)在S上是半正定的。 2)当7fx)在S上是正定矩阵时，f是S上的严格凸函数。（注：逆命题不成立） 9

9 2 2 2 2 1 1 2 1 2 2 2 2 2 2 1 2 2 2 2 2 2 1 2 ( ) ( ) ( ) .... ( ) ( ) ( ) ... ( ) ( ) ( ) ( ) n n n n n f x f x f x x x x x x f x f x f x x x x x x f x f x f x f x x x x x x                      =           1 2 ( ) ( ) ( ) ( ) n f x x f x f x x f x x               =               定理(凸函数的一阶充要条件) 若 f(x)在 S 上可微，则 f(x)是凸函 数当且仅当 ( ) ( ) ( ) ( ) T f x f x f x x x  +  − ，  x S 定理(凸函数的二阶充要条件) 设 f : S  R 二阶连续可导，则 1)f 是 S 上的凸函数的充要条件是 f 的 Hesse 矩阵 ( ) 2  f x 在 S 上是半正定的。 2)当 ( ) 2  f x 在 S 上是正定矩阵时，f 是 S 上的严格凸函数。(注:逆命题不成立)

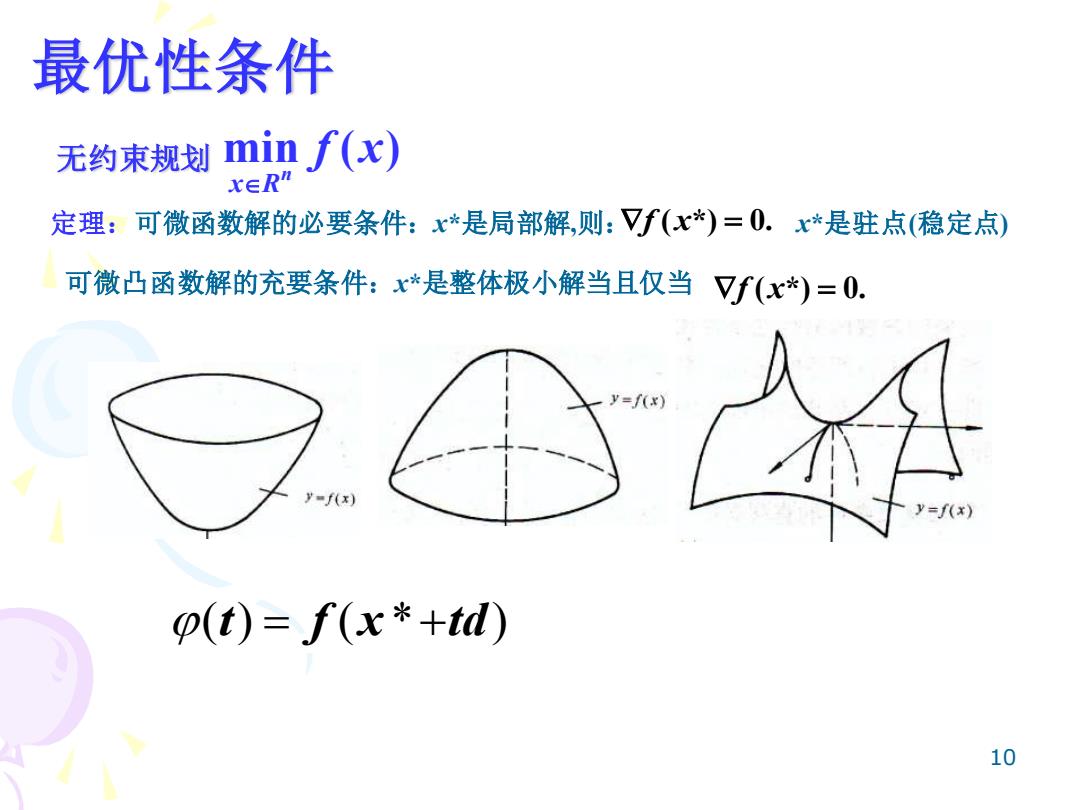
最优性条件 无约束规划 min f(x) r∈Rn 定理：可微函数解的必要条件：x*是局部解，则：Vf(x*)=0.x*是驻点（稳定点） 可微凸函数解的充要条件：x*是整体极小解当且仅当☑f(x*)=0. y=f(x) f八x) y=f(x) (t)=f(x*+td) 10

10 定理：可微函数解的必要条件：x*是局部解,则：  = f x( *) 0. 最优性条件 min ( ) n x R f x  无约束规划 x*是驻点(稳定点) 可微凸函数解的充要条件：x*是整体极小解当且仅当  = f x( *) 0. ( ) ( * ) t f x td = +

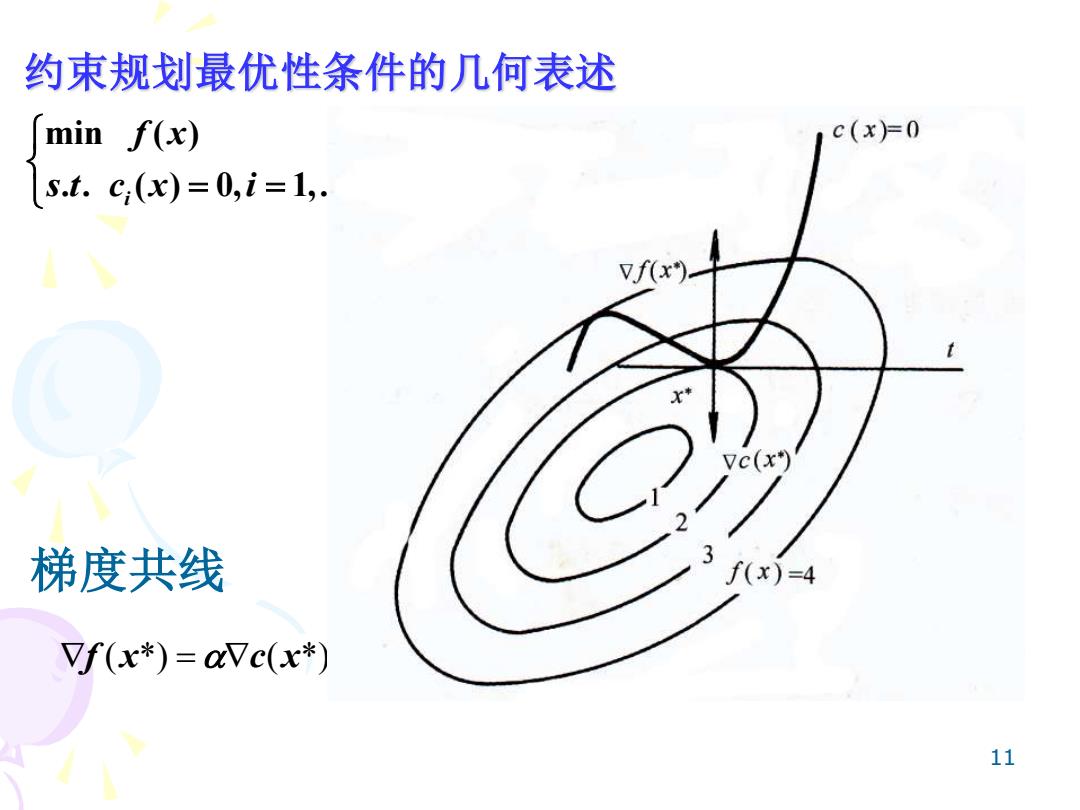
约束规划最优性条件的几何表述 min f(x) c(x)=0 s.t.c,(x)=0,i=1,. Vf(x) 梯度共线 f(x)=4 Vf(x*)=avc(x*) 11

11 约束规划最优性条件的几何表述 min ( ) . . ( ) 0, 1,..., i f x s t c x i q    = = 梯度共线  =  f x c x ( *) ( *) 