微分方程模型 0、简例 1、人口预报问题 2、传染病问题 3、作战模型 4、捕食问题 5、火箭发射问题 6、药物吸收、真假绘画作品鉴定、 交通管理/堵塞问题 ■■
微分方程模型 1、人口预报问题 3、作战模型 4、捕食问题 5、火箭发射问题 ……… 2、传染病问题 6、药物吸收、真假绘画作品鉴定、 交通管理/堵塞问题 0、简例
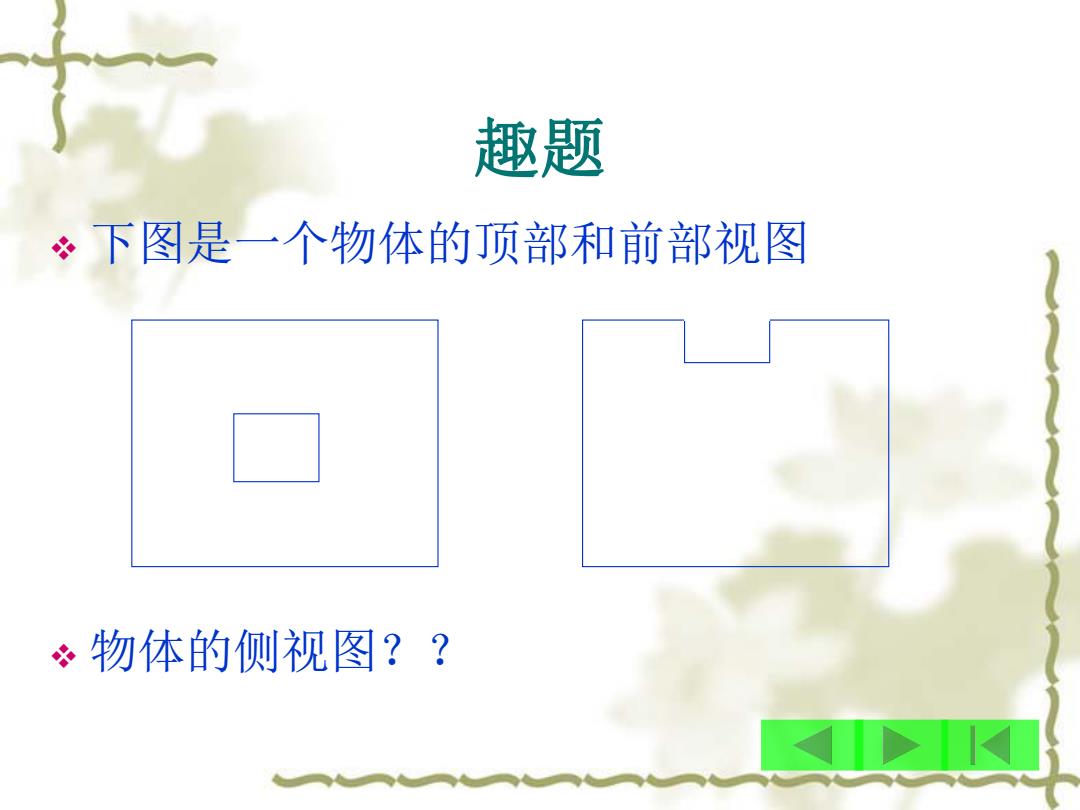
趣题 ·下图是一个物体的顶部和前部视图 。物体的侧视图??
趣题 v 下图是一个物体的顶部和前部视图 v 物体的侧视图??
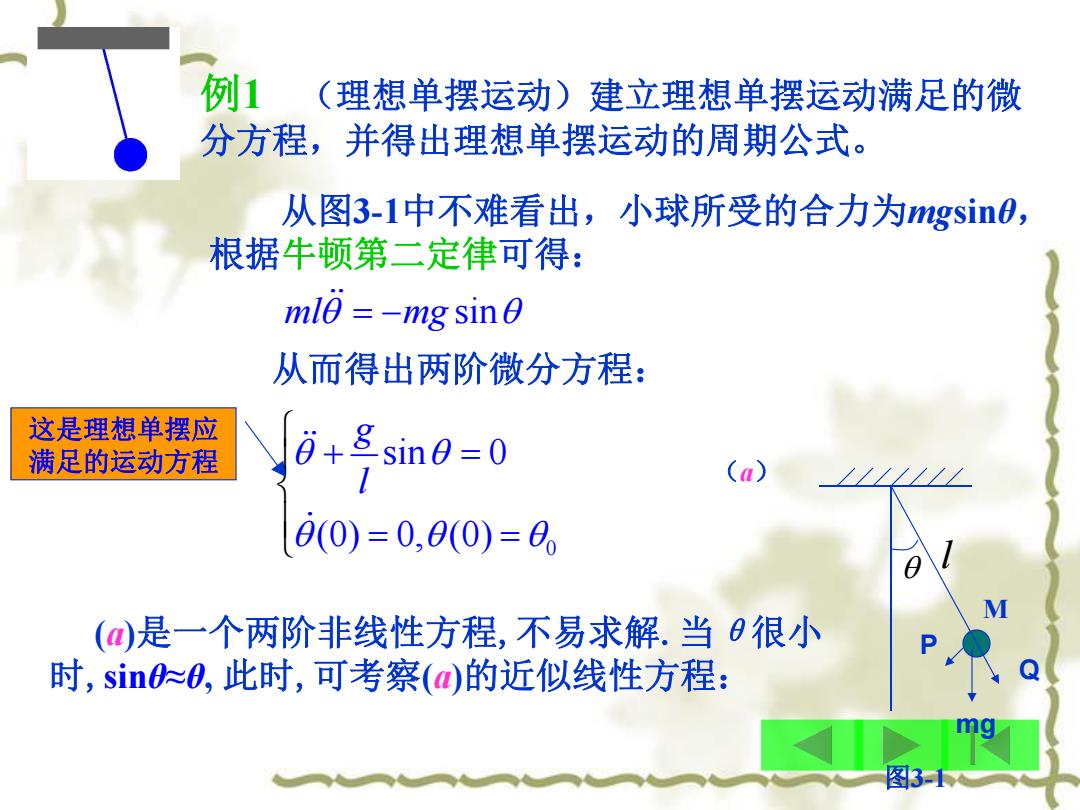
例1 (理想单摆运动)建立理想单摆运动满足的微 分方程,并得出理想单摆运动的周期公式。 从图3-1中不难看出,小球所受的合力为ngsin0, 根据牛顿第二定律可得: mle =-mg sin 从而得出两阶微分方程: 这是理想单摆应 满足的运动方程 6+sin0=0 a) 0(0)=0,0(0)=0 (是一个两阶非线性方程,不易求解,当0很小 时,sin~0,此时,可考察(的近似线性方程: g
例1 (理想单摆运动)建立理想单摆运动满足的微 分方程,并得出理想单摆运动的周期公式。 从图3-1中不难看出,小球所受的合力为mgsinθ, 根据牛顿第二定律可得: ml mg sin 从而得出两阶微分方程: 0 sin 0 (0) 0, (0) g l (a) 这是理想单摆应 满足的运动方程 (a)是一个两阶非线性方程,不易求解.当θ很小 时,sinθ≈θ, 此时,可考察(a)的近似线性方程: M Q P mg l 图3-1
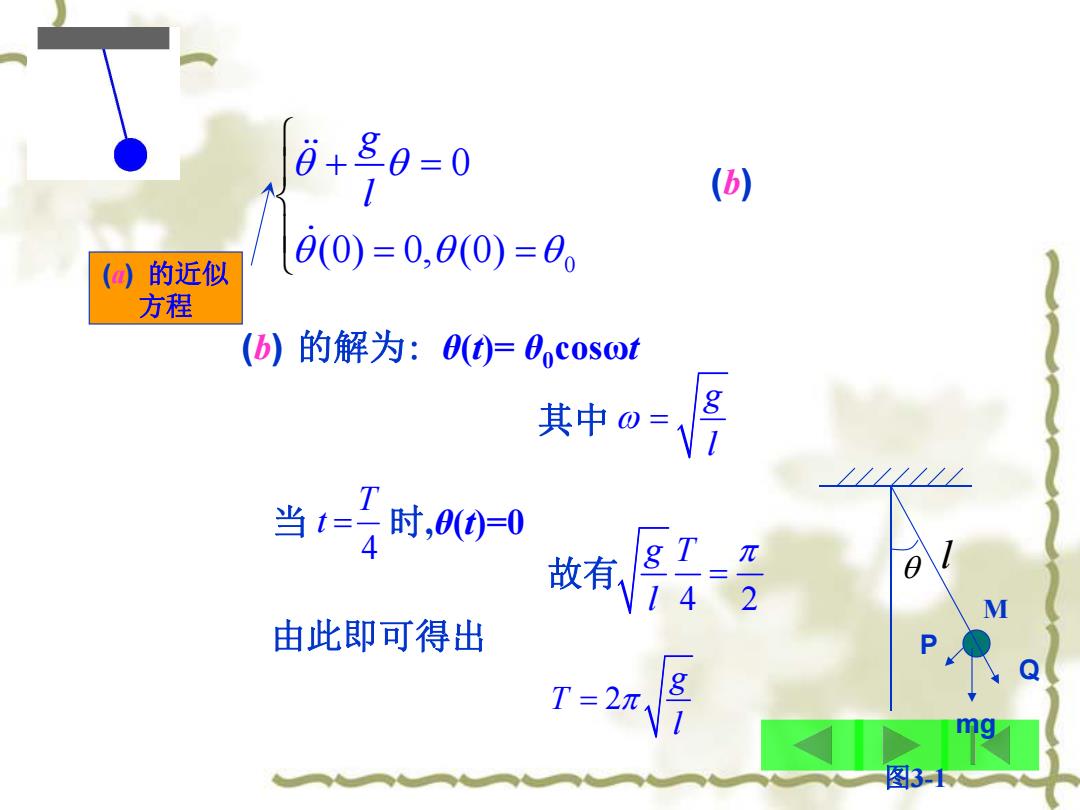
6+80=0 () ()的近似 0(0)=0,0(0)=8 方程 (b)的解为:0()=0ocos@t 其中o三的 当1=乙时,0c-0 4 故有、 T 2 14 由此即可得出 g T=2π mg 图31
0 0 (0) 0, (0) g l (b) 由此即可得出 2 g T l (b) 的解为: θ(t)= θ0cosωt g l 其中 当 时,θ(t)=0 4 T t 4 2 g T l 故有 M Q P mg l 图3-1 (a) 的近似 方程

例2市场价格模型 对于纯粹的市场经济来说,商品市场价格取决于市场供需之 间的关系,市场价格能促使商品的供给与需求相等(这样的价格 称为(静态)均衡价格)也就是说,如果不考虑商品价格形成的动 态过程,那么商品的市场价格应能保证市场的供需平衡,但是,实 际的市场价格不会恰好等于均衡价格,而且价格也不会是静态的, 应是随时间不断变化的动态过程.建立描述市场价格形成的动 态过程的数学模型。 假设在某一时刻t,商品的价格为p(),它与该商品的均衡价 格间有差别,此时,存在供需差,此供需差促使价格变动.对新的 价格,又有新的供需差,如此不断调节,就构成市场价格形成的 动态过程,假设价格p()的变化率dp/dt与需求和供给之差成正 比,并记fp)为需求函数,gp)为供给函数,于是 =k[f(p-g(p] dt
例2 市场价格模型 对于纯粹的市场经济来说,商品市场价格取决于市场供需之 间的关系,市场价格能促使商品的供给与需求相等(这样的价格 称为(静态)均衡价格).也就是说,如果不考虑商品价格形成的动 态过程,那么商品的市场价格应能保证市场的供需平衡,但是,实 际的市场价格不会恰好等于均衡价格,而且价格也不会是静态的, 应是随时间不断变化的动态过程. 建立描述市场价格形成的动 态过程的数学模型。 d d p k f p g p t 假设在某一时刻 t, 商品的价格为 p(t), 它与该商品的均衡价 格间有差别, 此时, 存在供需差, 此供需差促使价格变动. 对新的 价格, 又有新的供需差, 如此不断调节, 就构成市场价格形成的 动态过程, 假设价格p(t)的变化率dp/dt 与需求和供给之差成正 比, 并记 f(p) 为需求函数, g(p) 为供给函数, 于是

其中飞为参数.一般我们假设需求与价格呈负线形关系,而 供给与价格呈正线性关系,故可设f(p)=-ap+4,g(p)=bp+b, 则上式变为 =-k(a,+b)p+k(a,-b,) dt 其中41,a2,b,b2均为正常数,其通解为 p()=cea+4r+马3-b a +b 其中c=p。-p*为任意常数,可用初值条件确定
其中 k 为参数. 一般我们假设需求与价格呈负线形关系,而 供给与价格呈正线性关系,故可设 , 则上式变为 1 2 f ( p) a p a 1 2 g( p) b p b 1 1 2 2 d ( ) ( ) d p k a b p k a b t 其中 a1 , a2 ,b1 ,b2 均为正常数,其通解为 1 1 ( ) 2 2 1 1 ( ) e k a b t a b p t c a b 其中 为任意常数,可用初值条件确定。 0 c p p *

令f→+0,得 p=limp0=马-,这就是(静态) a +b 均衡价格,显然它满足 f(p*)=g(p*) 即供需到达平衡。初始价格高于均衡价 格时,动态价格就要逐步降低,且单调趋近均 衡价格;初始价格低于均衡价格时,动态价格 就要逐步升高,单调趋近均衡价格.进一步还 可以分析出,若初始价格等于均衡价格,整个 动态价格应保持不变
令 ,得 ,这就是(静态) 均衡价格,显然它满足 ——即供需到达平衡。初始价格高于均衡价 格时, 动态价格就要逐步降低, 且单调趋近均 衡价格; 初始价格低于均衡价格时, 动态价格 就要逐步升高, 单调趋近均衡价格. 进一步还 可以分析出, 若初始价格等于均衡价格, 整个 动态价格应保持不变. t 2 2 1 1 * lim ( ) t a b p p t a b f ( p*) g( p*)

建模示例1如何预报人口的增长 Malthus模型与Logistic模型 为了保持自然资料的合理开发与利用,人类必须保持并控 制生态平衡,甚至必须控制人类自身的增长。 这里针对单种群增长模型,简略分析一下这方面的问题。 一般复杂生态系统的分析可以通过一些简单模型的复合来研究, 大家若有兴趣可以根据生态系统的特征自行建立相应的模型。 美丽的大自然 种群的数量本应取离散值,但由于种群数 量一般较大,可将种群数量看作连续变量,甚 至允许它为可微变量,由此引起的误差将是十 分微小的,讨论其变化率,建立微分方程模型! 离散化为连续,方便研究
为了保持自然资料的合理开发与利用,人类必须保持并控 制生态平衡,甚至必须控制人类自身的增长。 这里针对单种群增长模型,简略分析一下这方面的问题。 一般复杂生态系统的分析可以通过一些简单模型的复合来研究, 大家若有兴趣可以根据生态系统的特征自行建立相应的模型。 美丽的大自然 种群的数量本应取离散值,但由于种群数 量一般较大,可将种群数量看作连续变量,甚 至允许它为可微变量,由此引起的误差将是十 分微小的,讨论其变化率,建立微分方程模型! 离散化为连续,方便研究 建模示例1 如何预报人口的增长 ——Malthus模型与Logistic模型
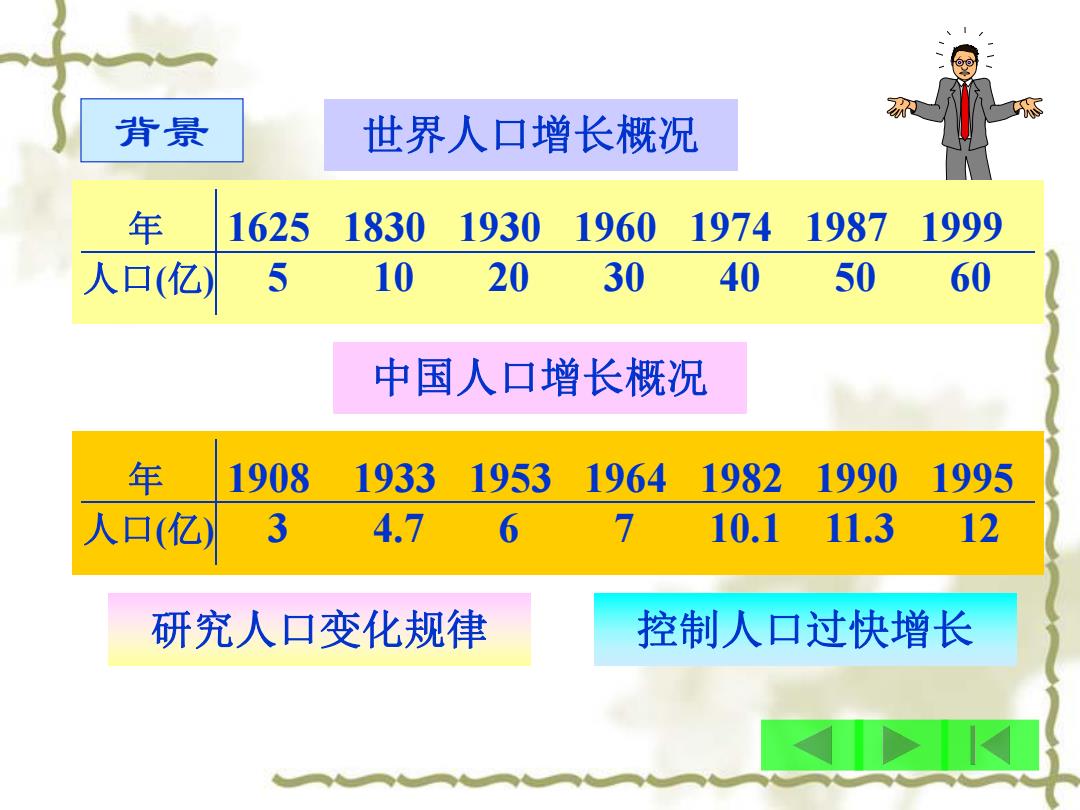
背景 世界人口增长概况 年 1625 1830 1930 1960 19741987 1999 人口(亿) 5 10 20 30 40 50 60 中国人口增长概况 年 1908 1933 1953 1964 1982 1990 1995 人口(亿) 3 4.7 6 7 10.111.3 12 研究人口变化规律 控制人口过快增长
背景 年 1625 1830 1930 1960 1974 1987 1999 人口(亿) 5 10 20 30 40 50 60 世界人口增长概况 中国人口增长概况 年 1908 1933 1953 1964 1982 1990 1995 人口(亿) 3 4.7 6 7 10.1 11.3 12 研究人口变化规律 控制人口过快增长

模型一:指数增长模型Malthus模型) 常用的计算公式 今年人口o,年增长率r k年后人口 x=北(1+r) 马尔萨斯(1788-1834)提出的指数增长模型(1798) x()时刻t人口 r~人口(相对)增长率(常数) x(t+△t)-x(t)=x(t)△t x(t)=xe dx =x,x(0)=x0 dt xt)=x(e)'≈xI+r 随着时间增加人口按指数规律无限增长!
模型一:指数增长模型(Malthus模型 ) 常用的计算公式 k k x x (1 r) 0 马尔萨斯(1788--1834)提出的指数增长模型(1798) x(t) ~时刻t人口 r ~ 人口(相对)增长率(常数) x(t t) x(t) rx(t)t 今年人口 x0 , 年增长率 r k年后人口 0 rx, x(0) x dt dx rt x t x e0 ( ) r t x(t) x (e ) 0 t x (1 r) 0 随着时间增加人口按指数规律无限增长!