
定积分的应用 第五章 单变量函数的积分学 1、什么问题可以用定积分解决? ① 所求的未知量Q具有整体性,它依赖于某个区间[,b]上的变量 x,并且Q(x)=Q([a,x]); ② 未知量Q在区间上具有可加性:对Va≤a<B<y≤b有 Q([,B])+Q([B,y])=Q([o,y]) 即当区间[a,b]被分成几个不重迭的区间之并时,总量Q([a,b]) 等于相应于各子区间的局部量的和. 未知量Q在区间[☑,b]上是可微的:局部量有线性主部. 2
2 定积分的应用 第五章 单变量函数的积分学 即当区间 被分成几个不重迭的区间之并时,总量 1、什么问题可以用定积分解决 ? ① 所求的未知量 具有整体性,它依赖于某个区间 上的变量 并且 ② 未知量 在区间上具有可加性 : 对 有 等于相应于各子区间的局部量的和. ③ 未知量 在区间 上是可微的: 局部量有线性主部

定积分的应用 第五章 单变量函数的积分学 在具体求这种未知量Q时,可以分两个步骤 1.在区间[a,上任取-个长度为dx的小区间[x,x+dx],求出与 此小区间相关的局部量△Q=Q(x+dx)-Q(x)的一个近似值 f(x)dx,其中f(x)是某个函数,使得 △Q=f(x)dx+o(dx), 即f(x)dx是函数Q(x)的微分,也称为微元. 2.将所得的微元在区间[☑,b]上无限累加"---积分,则 =∫fax)dx 微元法的关键在于确定微元.因为量Q是待求的,一般而言,求出 Q(x)的微分,即Q(x)的线性主要部分,是一件相当困难的事
3 定积分的应用 第五章 单变量函数的积分学 即 是函数 的微分,也称为微元. 在具体求这种未知量 时,可以分两个步骤 : 1. 在区间 上任取一个长度为 的小区间 求出与 此小区间相关的局部量 的一个近似值 其中 是某个函数,使得 微元法的关键在于确定微元. 因为量 是待求的, 一般而言,求出 的微分, 即 的线性主要部分, 是一件相当困难的事. 2. 将所得的微元在区间 上``无限累加''------积分, 则
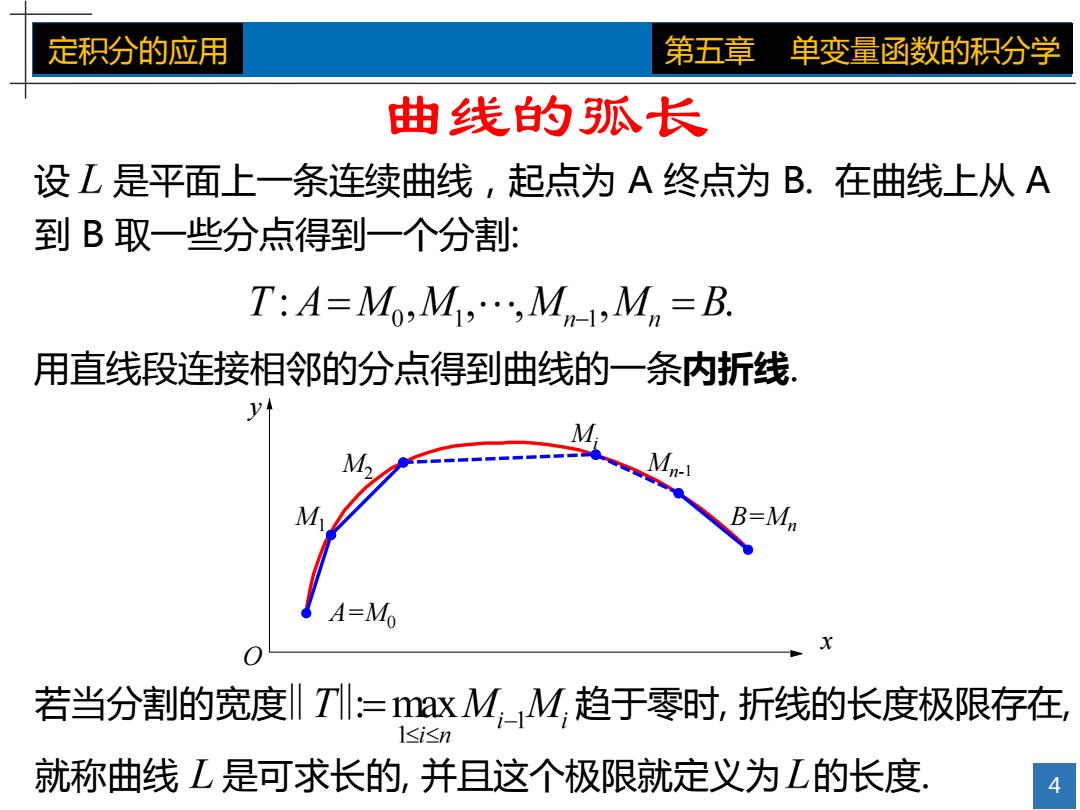
定积分的应用 第五章 单变量函数的积分学 曲线的孤长 设L是平面上一条连续曲线,起点为A终点为B.在曲线上从A 到B取一些分点得到一个分割: T:A=Mo,M,…,Mn,Mn=B. 用直线段连接相邻的分点得到曲线的一条内折线: Mn-i B=Mn A=Mo 若当分割的宽度Tl:=max M_M,趋于零时,折线的长度极限存在, l≤i≤n 就称曲线L是可求长的,并且这个极限就定义为L的长度
4 定积分的应用 第五章 单变量函数的积分学 设 是平面上一条连续曲线,起点为 A 终点为 B. 在曲线上从 A 到 B 取一些分点得到一个分割: 用直线段连接相邻的分点得到曲线的一条内折线. y M1 M2 Mi Mn-1 B=Mn A=M0 O x 曲线的弧长 若当分割的宽度 趋于零时, 折线的长度极限存在, 就称曲线 是可求长的, 并且这个极限就定义为 的长度

定积分的应用 第五章 单变量函数的积分学 设函数f(x)的图像为曲线L.设dx>0,在L上任取两点M和M', 其横坐标分别为x与x+dx.则这两点的距离为 MM'|=V(d)2+(f(x+dx)-f(x)2 =/(dx)2+(f(x)dx+o(dx))2 =V1+(f'(x)2dr+o(dr). 我们由此得到弧长的微元(即弧长的微分) ds=+f(x))dx. 5
5 定积分的应用 第五章 单变量函数的积分学 设函数 的图像为曲线 . 设 在 上任取两点 和 其横坐标分别为 与 则这两点的距离为 我们由此得到弧长的微元 (即弧长的微分)
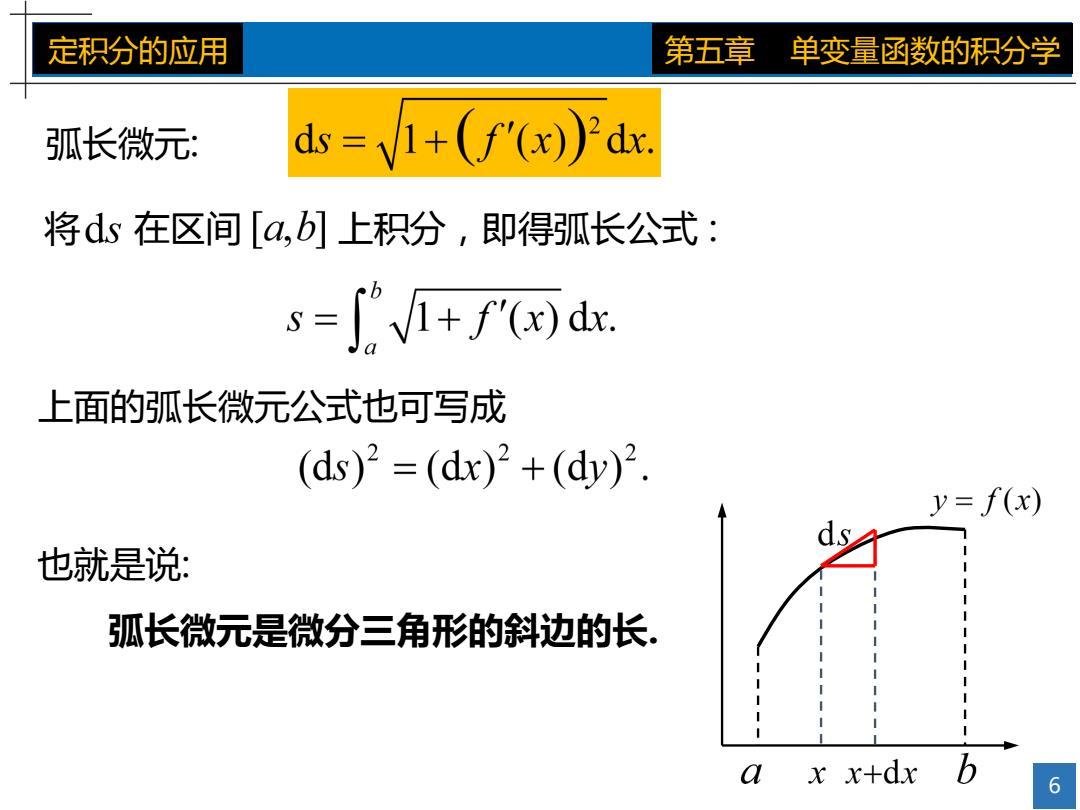
定积分的应用 第五章 单变量函数的积分学 弧长微元: ds=1+(f(x))dx. 将ds在区间[a,b]上积分,即得弧长公式: s=∫V1+f()d. 上面的弧长微元公式也可写成 (ds)2=(dx)2+(dy)2. y= f(x) ds 也就是说: 弧长微元是微分三角形的斜边的长。 xx+dx b 6
6 定积分的应用 第五章 单变量函数的积分学 将 在区间 上积分,即得弧长公式 : 也就是说: 上面的弧长微元公式也可写成 弧长微元: 弧长微元是微分三角形的斜边的长. y O x

定积分的应用 第五章 单变量函数的积分学 参数曲线的弧长 设曲线由参数方程 8as例给甜,脚a0w在 [a,B]上有连续导数.弧长微元为: ds =/(dx)2+(dy)2=()+w(t)di. 故弧长为:s=∫Vp()+y()d 特别地,对极坐标曲线r=r(θ)(≤0≤),设r(0)连续可导,则 曲线有参数化(x,y)=(r(0)cosO,r(0)sinO),代入上式可得: s=vf产(0)+(f(ada. 7
7 定积分的应用 第五章 单变量函数的积分学 设曲线由参数方程 给出,其中 在 参数曲线的弧长 : 上有连续导数. 弧长微元为 : 故弧长为 : 特别地,对极坐标曲线 设 连续可导,则 曲线有参数化 代入上式可得 :

定积分的应用 第五章 单变量函数的积分学 3 2 1.求曲线y=一x2上相应于x从1到2的一段弧的长度, 3 2.求旋轮线x=a(t-sint),y=a(1-cost)一支的弧长. x2 3.求椭圆 21的周长 8
8 定积分的应用 第五章 单变量函数的积分学 2. 求旋轮线 一支的弧长. 1. 求曲线 上相应于 从1到2的一段弧的长度. 3. 求椭圆 的周长
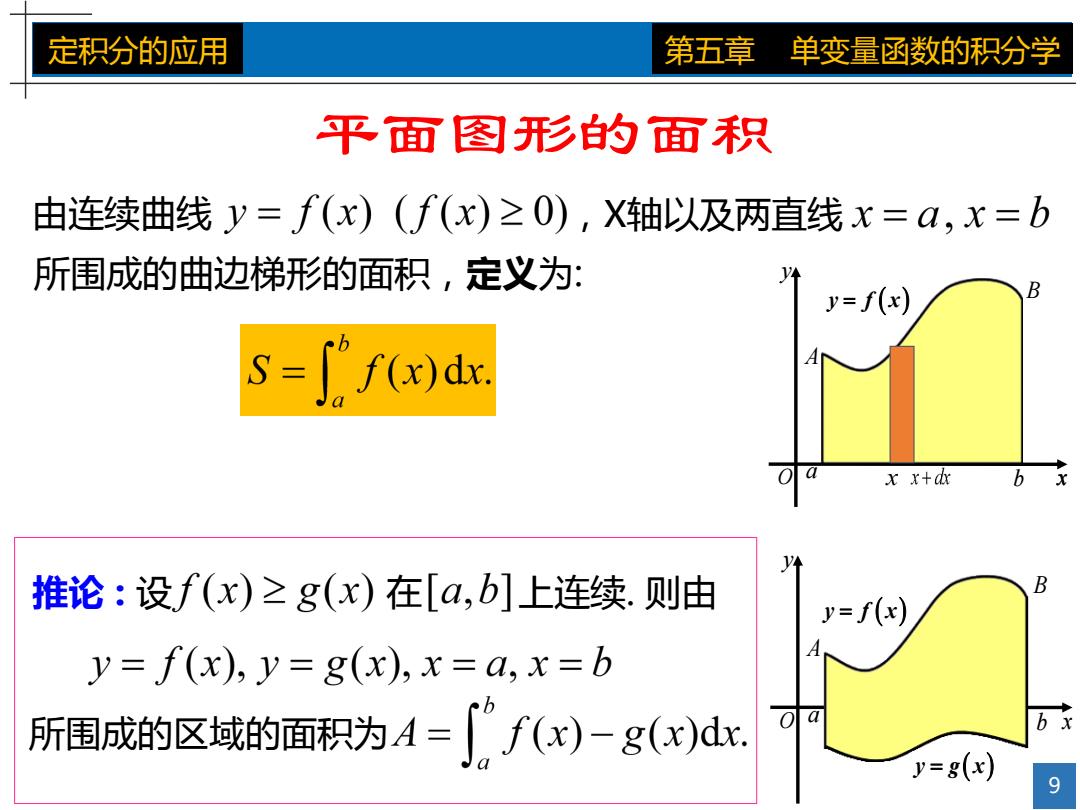
定积分的应用 第五章 单变量函数的积分学 平面图形的面积 由连续曲线y=f(x)(f(x)≥0),X轴以及两直线x=a,x=b 所围成的曲边梯形的面积,定义为: y=f(x) S=∫fx)dx xx+dx 6 推论:设f(x)≥g(x)在[a,b]上连续.则由 B y= f y=f(x),y=g(x),x=a,x=b 所围成的区域的面积为A=f(x)-g(x)dx y=g(x) 9
9 定积分的应用 第五章 单变量函数的积分学 平面图形的面积 由连续曲线 ,X轴以及两直线 所围成的曲边梯形的面积,定义为: 推论 : 设 在 上连续. 则由 所围成的区域的面积为 b a x A B x y O y f x y O x A B b a y g x y f x
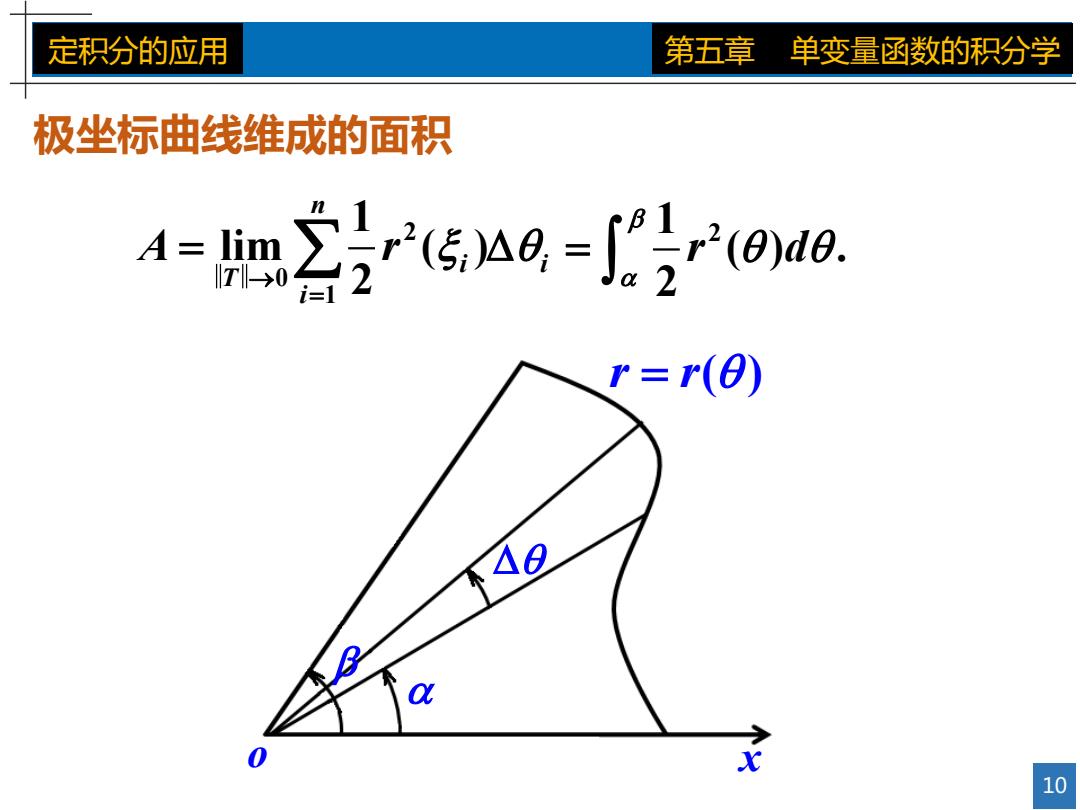
定积分的应用 第五章 单变量函数的积分学 极坐标曲线维成的面积 A=lim T‖→0 传ag=r(oa0, i1 r=r() 40 B a → 0 10
10 定积分的应用 第五章 单变量函数的积分学 x o r r ( ) 极坐标曲线维成的面积 2 0 1 1 lim ( ) 2 n i i T i A r 1 2 ( ) . 2 r d

定积分的应用 第五章 单变量函数的积分学 参数方程的图形所围成的区域的面积 设平面区域由闭曲线x=p(t),y=W(t)(≤t≤B)围成.p(t),w(t) 一阶连续可导.增加时,(x,y)在曲线上逆时针行走 x2+y2=r2(0) 0=arctan →d0= xy,-xy dt x2+y2 X A-(Ondo-(-)d 11
11 定积分的应用 第五章 单变量函数的积分学 参数方程的图形所围成的区域的面积 设平面区域由闭曲线 围成. 一阶连续可导. 增加时, 在曲线上逆时针行走. 2 2 2 ( ) arctan r x x y y ' ' 2 2 d d t t xy x y t x y 1 2 A ( ) 2 r d