
中国辩空我术大学 University of Science and Technology of China 第四章不定积分 §4.1 不定积分及基本计算方法 §4.2 有理函数的不定积分 育 創 天下 寰宇 英 學 府
1 第四章 不定积分 第四章 不定积分 §4.1 不定积分及基本计算方法 §4.2 有理函数的不定积分

第四章 不定积分 定义(原函数):f(x)在区间I上有定义.若存在F(x)使得在I上 F'(x)=f(x),则称F(x)是f(x)在I上的一个原函数. 注:1.I为闭区间时,在端点处的导数为单侧导数: 2.原函数与定义域有关 的原函数是lnx,还是ln(-)? X 3.原函数可能不存在,例如当f(x)在I上有第一类间断点时. 连续函数一定有原函数, 4.若F(x)为f(x)在I上的原函数,则F(x)+C也是;反之, 若g(x)为f(x)在I上的另一原函数,则存在常数C使得 g(x)=F(x)+C
2 第四章 不定积分 定义(原函数): 在区间 上有定义 . 若存在 使得在 上 则称 是 在 上的一个原函数. 注: 1. 为闭区间时,在端点处的导数为单侧导数. 2. 原函数与定义域有关. 的原函数是 ,还是 ? 3. 原函数可能不存在,例如当 在 上有第一类间断点时. 4. 若 为 在 上的原函数,则 也是;反之, 连续函数一定有原函数. 若 为 在 上的另一原函数,则存在常数 使得
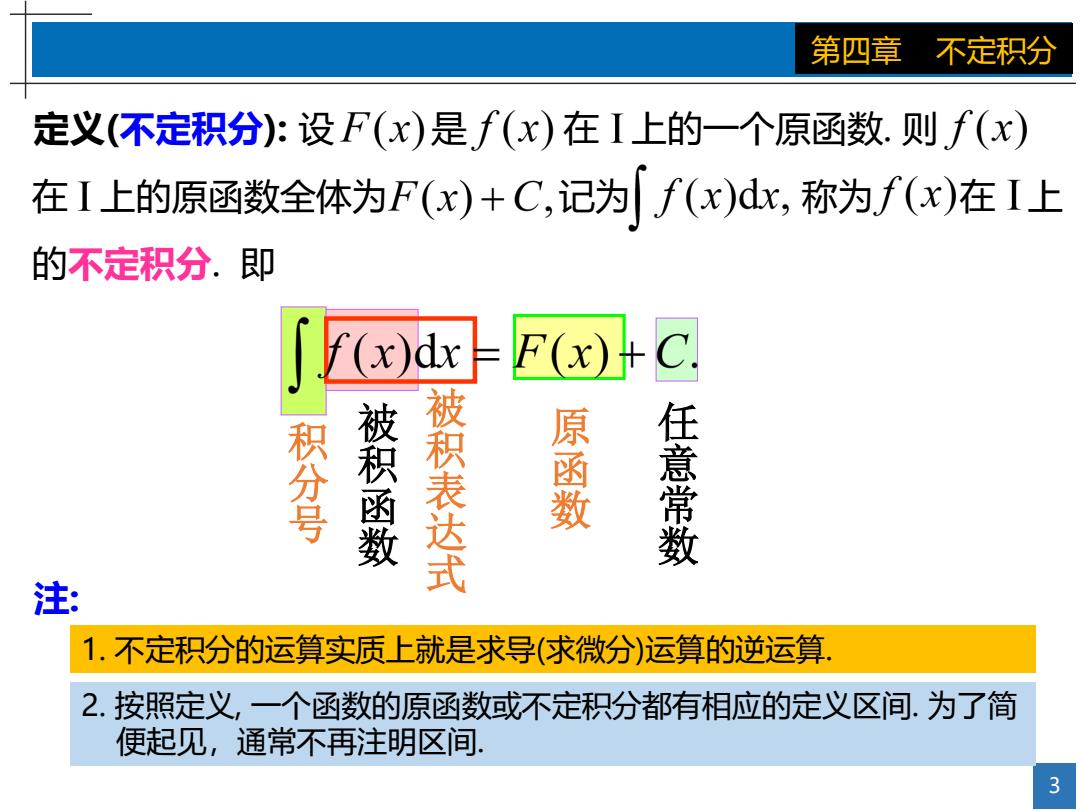
第四章 不定积分 定义(不定积分):设F(x)是f(x)在I上的一个原函数.则f(x) 在I上的原函数全体为F(x)+C,记为f(x)dx,称为f(x)在I上 的不定积分.即 ∫x)dFx+C 积分号 被积函数 被积表达式 原函数 任意常数 注 1.不定积分的运算实质上就是求导(求微分)运算的逆运算 2.按照定义,一个函数的原函数或不定积分都有相应的定义区间.为了简 便起见,通常不再注明区间 3
3 第四章 不定积分 定义(不定积分): 设 是 在 上的一个原函数. 则 在 上的原函数全体为 记为 称为 在 上 的不定积分. 即 1. 不定积分的运算实质上就是求导(求微分)运算的逆运算. 2. 按照定义, 一个函数的原函数或不定积分都有相应的定义区间. 为了简 便起见,通常不再注明区间. 注: 积 分 号 被 积 函 数 被 积 表 达 式 原 函 数 任 意 常 数
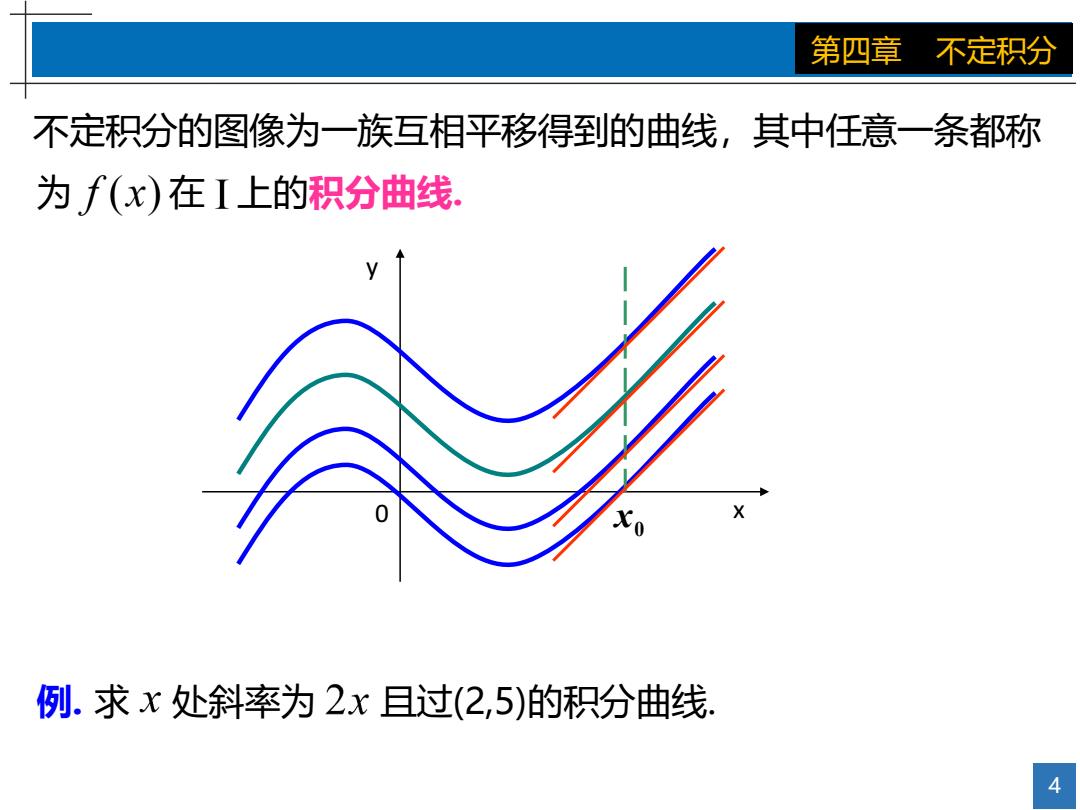
第四章 不定积分 不定积分的图像为一族互相平移得到的曲线,其中任意一条都称 为f(x)在I上的积分曲线. Xo X 例.求x处斜率为2x且过(2,5)的积分曲线 4
4 第四章 不定积分 不定积分的图像为一族互相平移得到的曲线,其中任意一条都称 为 在 上的积分曲线. 例. 求 处斜率为 且过(2,5)的积分曲线. 0 x y 0 x

第四章 不定积分 常见函数的不定积分 ()∫kdc=a+C(k是常数: (2) +c(u≠-1); u+1 (3)∫r=ne+e (④j十ts=aretanx+.Gi dx arcsinx+C; (⑥)∫cosxdx=sin.x+C; 5
5 第四章 不定积分 常见函数的不定积分 1 ( ) d ( k x kx C k 是常数); 1 2 1 1 ( ) d ( ); x x x c 3 d ( ) ln ; x x c x 2 1 4 1 ( ) dx x arctan x C; 2 1 5 1 ( ) dx x arcsin x C; 6 ( ) cos dx x sin x C;

第四章 不定积分 (7)∫sinxdx=-cosx+C; 周jox-fe-tanx+c: 网-fcsxu=-wtx+c (10)[secxtanxdx=secx+C; (11)[cscxcotxdx=-cscx+C; (12)「e*dx=e*+C; (13)fa'dx-c 6
6 第四章 不定积分 ( ) sin d 7 x x cos x C; 2 8 d ( ) cos x x 2 sec dx x tan x C; 2 9 d ( ) sin x x 2 csc dx x cot x C; ( ) sec tan d 10 x x x sec x C; ( ) csc cot d 11 x x x csc x C; ( ) d 12 x e x e C; x ( ) d 13 x a x ; ln C a a x

第四章 不定积分 不定积分的性质 (rd)- (2)∫F'(x)ds=F(x)+C. (③)j(f()±g(x)odk-jfx)a±∫sx)d (4)∫x)=k∫fx)adk 7
7 第四章 不定积分 (1). f x dx f x ( ) ( ). ( 2). ( F x dx F x C ) ( ) . (3). f x g x dx f x dx g x dx ( ) ( ) ( ) ( ) . (4). kf x dx k f x dx ( ) ( ) . 不定积分的性质

第四章 不定积分 ex2 -dx 5.Je"dx 6.∫max{L,xdxr 8
8 第四章 不定积分 2 4 1. 3 d x x x 2 3 1 2. d 1 x x x x 2 1 3. d x x x 2 2 1 cos 4. d sin x x x | | 5. dx e x 6. max{1, }d x x

第四章 不定积分 不定积分的计算方法 定理(凑微分法):设f(x)有原函数,t=p(x)可导,则 J(jf()dr-c+c =G(p(x)+C. 复合函数的求导 公式的逆. 32 2.[tan.xdx 9
9 第四章 不定积分 不定积分的计算方法 f x x x ( ) ( )d 定理 (凑微分法): 设 有原函数, 可导,则 f t t d t x ( ) G t C ( ) G x C ( ) . 例: 1 1 3 2 . dx x 3 3 1 . d . ( ) x x x 2 . tan dx x 2 2 1 4 . dx a x 复合函数的求导 公式的逆

第四章 不定积分 利用基本积分表的公式把被积函数中的一部分凑成中间变量的微 分,常见的有: dx-id(ax+B) rar=a(r) Idx =d(Inlx D; e*dx =d(e*) X a*dx 1da*) cosxdx=d(sinx) In a sinxdx =-d(cosx) sec xdx =d(tanx) csc xdx =-d(cotx) d-d(aresin )=-d(arecos x) 1+2 dx=d(arctanx)=-d(arccotx) 10
10 第四章 不定积分 利用基本积分表的公式把被积函数中的一部分凑成中间变量的微 分,常见的有: 1 2 2 2 2 1 1 d d d d 1 d d(ln | |); d d( ) 1 d d( ) cos d d(sin ) ln sin d d(cos ) sec d d(tan ) csc d d(cot ) 1 d d(arcsin ) d(arccos ) 1 1 d d(arctan ) d( cot ) 1 n n x x x x x ax b x x x a n x x e x e x a x a x x x a x x x x x x x x x x x x x x x arc x x