
离散数学 第三部分图论 本部分主要内容 图的基本概念 ·树 欧拉图与哈密顿图 二部图与匹配 ● 平面图 着色 1
1 第三部分 图论 本部分主要内容 ⚫ 图的基本概念 ⚫ 树 ⚫ 欧拉图与哈密顿图 ⚫ 二部图与匹配 ⚫ 平面图 ⚫ 着色

离散数学 第十一章图的基本概念 主要内容 ●图 ● 通路与回路 图的连通性 图的矩阵表示 预备知识 ● 多重集合一一元素可以重复出现的集合 ● 无序集一一A&B={cy)川x∈Ay∈B} 2
2 第十一章 图的基本概念 主要内容 ⚫ 图 ⚫ 通路与回路 ⚫ 图的连通性 ⚫ 图的矩阵表示 预备知识 ⚫ 多重集合——元素可以重复出现的集合 ⚫ 无序集——AB={(x,y) | xAyB}
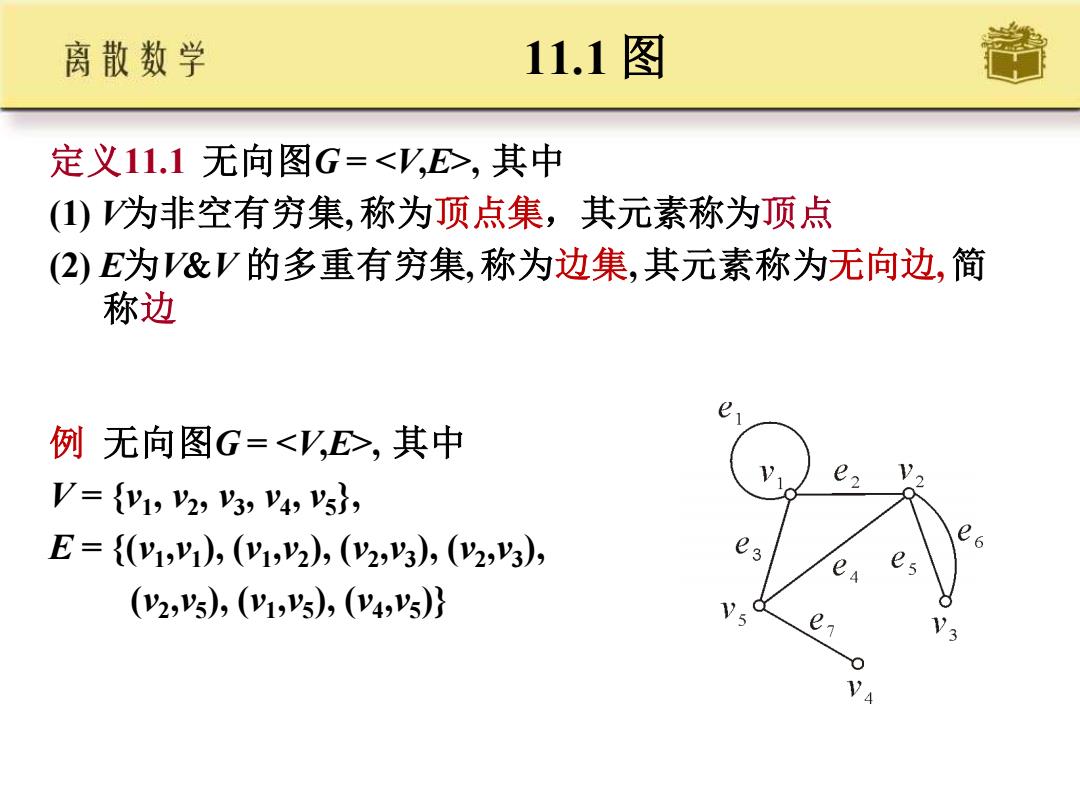
离散数学 11.1图 定义11.1无向图G=,其中 ()为非空有穷集,称为顶点集,其元素称为顶点 (2)E为V&V的多重有穷集,称为边集,其元素称为无向边,简 称边 例无向图G=,其中 V={y1,2,3,V4,s, E={(1,y1),(y12),(y2,3),((2,3), 0 (2,s),(y1,s),(y4,ys)} A
11.1 图 定义11.1 无向图G = , 其中 (1) V为非空有穷集, 称为顶点集,其元素称为顶点 (2) E为VV 的多重有穷集, 称为边集, 其元素称为无向边, 简 称边 例 无向图G = , 其中 V = {v1 , v2 , v3 , v4 , v5 }, E = {(v1 ,v1 ), (v1 ,v2 ), (v2 ,v3 ), (v2 ,v3 ), (v2 ,v5 ), (v1 ,v5 ), (v4 ,v5 )}

离散数学 有向图 定义11.2有向图D=,其中 ()Ψ为非空有穷集,称为顶点集,其元素称为顶点 (2)E为%V的多重有穷集,称为边集,其元素称为有向边,简 称边 例有向图D=,其中 b V-fa,b,c,dj E={,,,,} a 注意:图的集合表示与图形表示之间的对应 4
4 有向图 定义11.2 有向图D=,其中 (1) V 为非空有穷集, 称为顶点集,其元素称为顶点 (2) E为VV 的多重有穷集, 称为边集, 其元素称为有向边, 简 称边 例 有向图D=, 其中 V={a,b,c,d} E={,,,, ,,} 注意:图的集合表示与图形表示之间的对应

离散数学 相关概念 1.无向图和有向图通称图.记顶点集(G,边集E(G 2.图的阶,n阶图. 3.n阶零图N,平凡图N, 4.空图0. 5.标定图与非标定图. 6.有向图的基图. 7.无向图中顶点与边的关联及关联次数,顶点与顶点、边与 边的相邻关系. 8.有向图中顶点与边的关联,顶点与顶点、边与边的相邻关 系 9.环,孤立点。 5
5 相关概念 1. 无向图和有向图通称图. 记顶点集V(G), 边集E(G). 2. 图的阶, n阶图. 3. n 阶零图Nn , 平凡图N1 . 4. 空图. 5. 标定图与非标定图. 6. 有向图的基图. 7. 无向图中顶点与边的关联及关联次数, 顶点与顶点、边与 边的相邻关系. 8. 有向图中顶点与边的关联, 顶点与顶点、边与边的相邻关 系. 9. 环, 孤立点

离散数学 多重图与简单图 定义11.3无向图中关联同一对顶点的2条和2条以上的边称为 平行边.有向图中2条和2条以上始点、终点相同的边称为平 行边.平行边的条数称为重数 含平行边的图称为多重图,不含平行边和环的图称为简单图, 定义11.4设G=为无向图,HveV,称作为边的端点的次 数之和为v的度数,简称度,记作(吵 设D=为有向图,Vv∈y,称作为边的始点的次数之和 为的出度,记作(;称作为边的终点的次数之和为的入 度,记作(y);称(y)+t(y)为的度数,记作d(v), 6
6 多重图与简单图 定义11.3 无向图中关联同一对顶点的2条和2条以上的边称为 平行边. 有向图中2条和2条以上始点、终点相同的边称为平 行边. 平行边的条数称为重数. 含平行边的图称为多重图, 不含平行边和环的图称为简单图. 定义11.4 设G=为无向图, vV, 称v作为边的端点的次 数之和为v的度数, 简称度, 记作d(v). 设D=为有向图, vV, 称v作为边的始点的次数之和 为v的出度, 记作d + (v); 称v作为边的终点的次数之和为v的入 度, 记作d − (v); 称d + (v)+d − (v)为v的度数, 记作d(v)

离散数学 顶点的度数 设G=为无向图, G的最大度△(G)=max{d(v)川ve G的最小度G=min{d)川v∈乃 设D=为无向图, D的最大度(D)=max{d()川v∈ D的最小度D)=min{d(vy川ve D的最大出度(D)=max{(y)川v∈乃 D的最小出度δ+(D)=min{(y)lv∈ D的最大入度(D)=max{d()川v∈仍 D的最小入度6-(D)=min{(y)川v∈乃 悬挂顶点:度数为1的顶点,悬挂边:与悬挂顶点关联的边 偶度(奇度)顶点:度数为偶数(奇数)的顶点 7
7 顶点的度数 设G=为无向图, G的最大度(G)=max{d(v) | vV} G的最小度 (G)=min{d(v) | vV} 设D=为无向图, D的最大度(D)=max{d(v) | vV} D的最小度 (D)=min{d(v) | vV} D的最大出度 + (D)=max{d + (v) | vV} D的最小出度 + (D)=min{d + (v) | vV} D的最大入度 − (D)=max{d − (v) | vV} D的最小入度 − (D)=min{d − (v) | vV} 悬挂顶点: 度数为1的顶点, 悬挂边: 与悬挂顶点关联的边. 偶度(奇度)顶点: 度数为偶数(奇数)的顶点
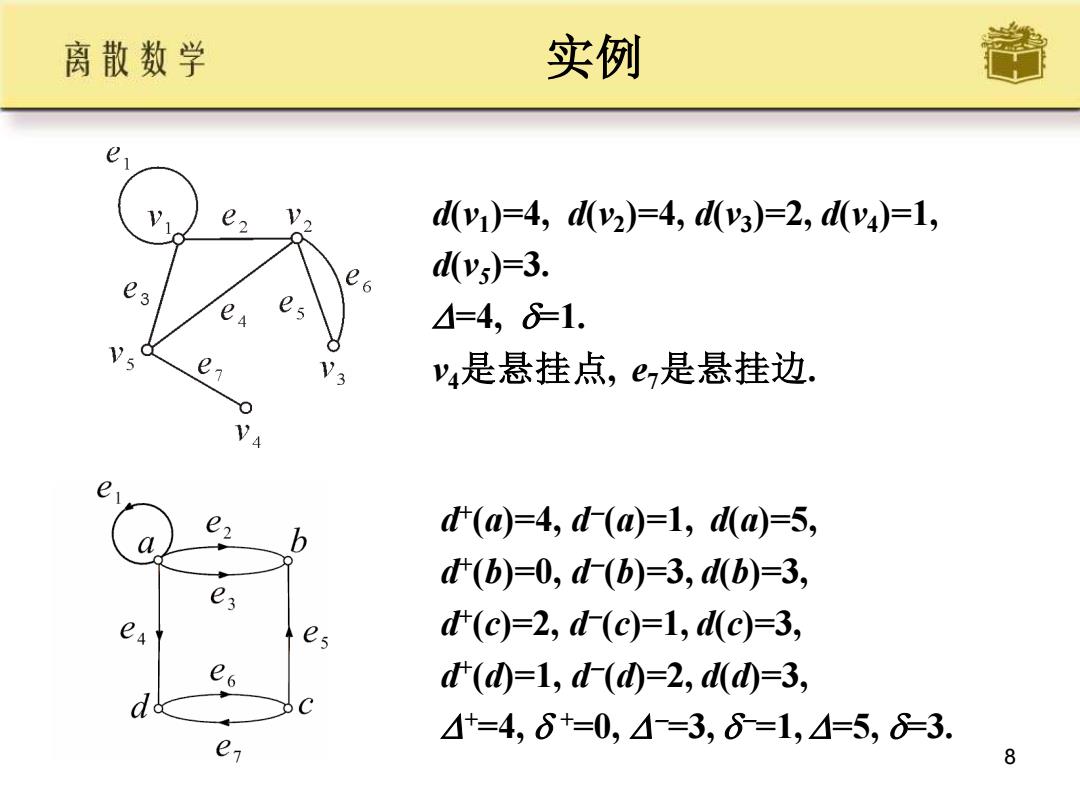
离散数学 实例 e e dy1)=4,d(y2)=4,dy3)=2,d(y4)=1, e6 dy5)=3. =4,1. e V3 y4是悬挂点,e是悬挂边. A e d(o)=4,d(o=1,do=5, b d(b)=0,d(b)=3,d(b)=3, 3 es d(c)=2,(c)=1,d(c)=3, d'(0=1,(d0=2,dd0=3, +=4,6+=0,=3,6=1,△=5,83. e 8
8 实例 d(v1 )=4, d(v2 )=4, d(v3 )=2, d(v4 )=1, d(v5 )=3. =4, =1. v4是悬挂点, e7是悬挂边. d + (a)=4, d − (a)=1, d(a)=5, d + (b)=0, d − (b)=3, d(b)=3, d + (c)=2, d − (c)=1, d(c)=3, d + (d)=1, d − (d)=2, d(d)=3, +=4, +=0, − =3, − =1, =5, =3

离散数学 握手定理 定理11.1在任何无向图中,所有顶点的度数之和等于边数的2倍 证G中每条边(包括环)均有两个端点,所以在计算G中各顶 点度数之和时,每条边均提供2度,m条边共提供2m度. 定理11.2在任何有向图中,所有顶点的度数之和等于边数的2倍; 所有顶点的入度之和等于所有顶点的出度之和,都等于边数: 推论任何图无向或有向)中,奇度顶点的个数是偶数, 证由握手定理,所有顶点的度数之和是偶数,而偶度顶点的度 数之和是偶数,故奇度顶点的度数之和也是偶数.所以奇度顶 点的个数必是偶数. 9
9 定理11.1 在任何无向图中, 所有顶点的度数之和等于边数的2倍. 证 G中每条边 (包括环) 均有两个端点,所以在计算G中各顶 点度数之和时,每条边均提供2度,m 条边共提供2m 度. 握手定理 定理11.2 在任何有向图中,所有顶点的度数之和等于边数的2倍; 所有顶点的入度之和等于所有顶点的出度之和, 都等于边数. 推论 任何图 (无向或有向) 中,奇度顶点的个数是偶数. 证 由握手定理, 所有顶点的度数之和是偶数, 而偶度顶点的度 数之和是偶数, 故奇度顶点的度数之和也是偶数. 所以奇度顶 点的个数必是偶数.

离散数学 握手定理应用 例1无向图G有16条边,3个4度顶点,4个3度顶点,其余 均为2度顶点度,问G的阶数n为几? 解本题的关键是应用握手定理, 设除3度与4度顶点外,还有x个顶点,由握手定理, 16×2=32=3×4+4×3+2x 解得x=4,阶数n=4+4+3=11. 例2在一个部门的25个人中间,由于意见不同,是否可能 每个人恰好与其他5个人意见一致? 解:不可能。考虑一个图,其中顶点代表人,如果两个 人意见相同,可用边连接,所以每个顶点都是奇数度。 存在奇数个度为奇数的图,这是不可能的。 定理11.3设G为任意n阶无向简单图,则4(G)≤n-1. 10
10 例1 无向图G有16条边,3个4度顶点,4个3度顶点,其余 均为2度顶点度,问G的阶数n为几? 解 本题的关键是应用握手定理. 设除3度与4度顶点外,还有x个顶点, 由握手定理, 162=32 = 34+43+2x 解得 x = 4, 阶数 n = 4+4+3=11. 握手定理应用 定理11.3 设G为任意n阶无向简单图,则(G)n−1. 例2 在一个部门的25个人中间,由于意见不同,是否可能 每个人恰好与其他5个人意见一致? 解:不可能。考虑一个图,其中顶点代表人,如果两个 人意见相同,可用边连接,所以每个顶点都是奇数度。 存在奇数个度为奇数的图,这是不可能的