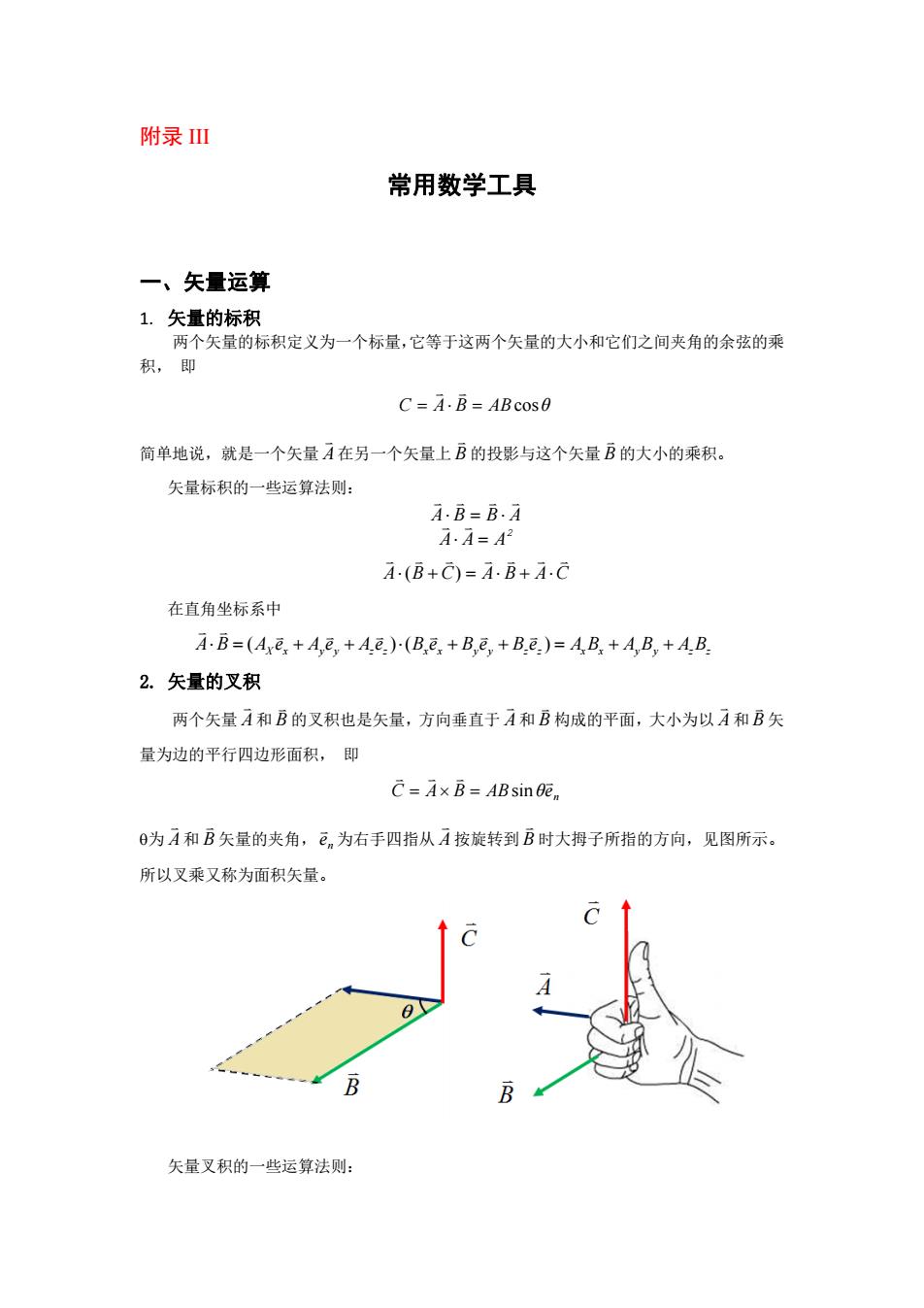
附绿川 常用数学工具 一、矢量运算 1.矢量的标积 两个矢量的标积定义为一个标量,它等于这两个矢量的大小和它们之间夹角的余弦的乘 积,即 C=A·B=ABcos0 简单地说,就是一个矢量A在另一个矢量上B的投影与这个矢量B的大小的乘积。 矢量标积的一些运算法则: A·B=B.A A·A=A2 4.(B+C)=4.B+4.C 在直角坐标系中 A.B=(Axe,+A,e,+A.e.)(Be,+B,,+B.e.)=AB,+A,B,+A.B. 2.矢量的叉积 两个矢量A和B的叉积也是矢量,方向垂直于A和B构成的平面,大小为以A和B矢 量为边的平行四边形面积,即 C=Ax B=ABsin 0e 日为A和B矢量的夹角,en为右手四指从A按旋转到B时大拇子所指的方向,见图所示。 所以叉乘又称为面积矢量。 B B 矢量叉积的一些运算法则:
附录 III 常用数学工具 一、矢量运算 1. 矢量的标积 两个矢量的标积定义为一个标量,它等于这两个矢量的大小和它们之间夹角的余弦的乘 积, 即 C A B AB cos θ 简单地说,就是一个矢量 A 在另一个矢量上 B 的投影与这个矢量 B 的大小的乘积。 矢量标积的一些运算法则: A B B A 2 A A A A B C A B A C ( ) 在直角坐标系中 ( )( ) A B A e Ae Ae Be Be Be AB AB AB X x yy zz xx yy zz x x y y z z 2. 矢量的叉积 两个矢量 A 和 B 的叉积也是矢量,方向垂直于 A 和 B 构成的平面,大小为以 A 和 B 矢 量为边的平行四边形面积, 即 n C A B AB e sin θ 为 A 和 B 矢量的夹角, n e 为右手四指从 A 按旋转到 B 时大拇子所指的方向,见图所示。 所以叉乘又称为面积矢量。 矢量叉积的一些运算法则:

A×B=-B×A A×A=0 A×(B+C)=A×B+A×C 在直角坐标系中 A×B=(Axe.+A,e,+Ae)×(BEx+B,E,+B.E:) =(A,B.-A.B )+(A.B,-A,B.)+(A,B -A,B )e. 此式也可以用一个很容易记忆的行列式表示,即 e,e, e A×B=AA, A B.BB. 3.矢量的其它运算公式 A(B×C)=C.(A×B)=B.(C×A Ax(B×C)=B(A.C)-C(A·B) (A×BxC=(AC)B-(B.C)A (A×B)·(C×D)=(A.C)(B.D)-(AD(B.C) 二、哈密顿(Hamilton)算符(或算子)“7” 引进微分算子“V”,读作“Nabla'”。在直角坐标系中,7为: 了=:x e,0y e:02 在柱坐标和球坐标系中,“V”的表达式为 反=e0m10 +eT00 0..10,.10 v=er or +oT00 +。 rsine 00 另外,还经常用到标量拉普拉斯算子,即又2=7.V 在直角坐标系中的拉普拉斯算子表达式为:了2=0+02+02 =x+0y+c2
A B B A - A A 0 A B C A B A C ( ) 在直角坐标系中 y z z y x z x x z y x y y x z X x y y z z x x y y z z A B A B e A B A B e A B A B e A B A e A e A e B e B e B e ( ) ( ) ( ) ( ) ( ) 此式也可以用一个很容易记忆的行列式表示,即 x y z x y z x y z B B B A A A e e e A B 3. 矢量的其它运算公式 A (B C) C (A B) B (C A) A (B C) B(A C) C(A B) A B C A C B B C A ( ) ( ) (A B) (C D) (A C)(B D) (A D)(B C) 二、哈密顿 (Hamilton) 算符(或算子) “” 引进微分算子“ ”,读作 “Nabla”。在直角坐标系中, 为: z e y e x ex y z 在柱坐标和球坐标系中,“ ”的表达式为 z e r e r er z 1 rsin e r e r er 1 1 另外,还经常用到标量拉普拉斯算子,即 2 在直角坐标系中的拉普拉斯算子表达式为: 2 2 2 2 2 2 2 x y z

在柱坐标系中和球坐标中拉普拉斯算子的表达式分别为 02 一(r一)+ ror or'r2 802 2s16 10 1 82 sin- r2 or or'r2sin0 00 0 r2sin20002 三、场论初步 若对全空间或其中某一区域V中每一点P,都有一个标量值(或矢量值)与之对应 则称在V上给定了一个标量场(或矢量场)。例如:温度和密度都是标量场,力和速度都 是矢量场。在引进直角坐标系后,点P的位置可由坐标确定;因此给定了某个标量场就等 于给定了一个标量函数低,y。在以下讨论中总是设它对每个变量都有一阶连续偏导数: 同理,每个矢量场都可用某个向量函数A表示,并假定它们有一阶连续偏导数,即 A(x,y,z)=A,(x,y,z)e,+A,(x,y,z)e,+A.(x,y,)e. 相对应,Ax,AA为所定义区域上的标量函数。 1.标量场的梯度 (1)梯度的定义 我们定义一个矢量A,其方向就是标量函数“在P点处变化率为最大的方向,其大小 就是这个最大变化率的值,这个矢量A称为函数u在P点处的梯度(gradient),记为 grad u=A=0 Ou 己可以用哈密顿算符表示,即 A=gard u=Vu Vu称梯度场。 (2)梯度的性质 梯度有以下重要性质: 1) 方向导数等于梯度在该方向上的投影即=V1i al 2) 标量场u中每一点P处的梯度,垂直于过该点的等值面,且指向函数P)增大的方 向。也就是说,梯度就是该等值面的法向矢量。 3) 7×71=0,这就是说如果一个矢量A满足7×A=0,即A是一个无旋场,则矢 量A可以用一个标量函数的梯度来表示,即A=V!。如静电场中的电场强度就可以用一个 标量函数静电势的梯度来表示。 2.矢量场的散度 (1)散度的定义 设有矢量场A,在场中任一点P处作一个包含P点在内的任一闭合曲面S,S所限定的
在柱坐标系中和球坐标中拉普拉斯算子的表达式分别为 2 2 2 2 2 2 1 1 r r z r r r φ ( ) 2 2 2 2 2 2 2 2 1 1 1 θ θ φ θ θ θ sin sin sin ( ) r r r r r r 三、场论初步 若对全空间或其中某一区域 V 中每一点 P, 都有一个标量值 (或矢量值) 与之对应, 则称在 V 上给定了一个标量场 (或矢量场)。 例如: 温度和密度都是标量场, 力和速度都 是矢量场。 在引进直角坐标系后, 点 P 的位置可由坐标确定; 因此给定了某个标量场就等 于给定了一个标量函数 u(x,y,z)。在以下讨论中总是设它对每个变量都有一阶连续偏导数; 同理, 每个矢量场都可用某个向量函数 A 表示, 并假定它们有一阶连续偏导数,即 x x y y z z A x y z A x y z e A x y z e A x y z e ( , , ) ( , , ) ( , , ) ( , , ) 相对应,Ax, Ay, Az 为所定义区域上的标量函数。 1. 标量场的梯度 (1)梯度的定义 我们定义一个矢量 A ,其方向就是标量函数 u 在 P 点处变化率为最大的方向,其大小 就是这个最大变化率的值,这个矢量 A 称为函数 u 在 P 点处的梯度(gradient),记为 x y z e z u e y u e x u grad A u 已可以用哈密顿算符表示,即 A gard u u u 称梯度场。 (2) 梯度的性质 梯度有以下重要性质: 1) 方向导数等于梯度在该方向上的投影即 u l l u 2) 标量场 u 中每一点 P 处的梯度,垂直于过该点的等值面,且指向函数 u(P)增大的方 向。也就是说,梯度就是该等值面的法向矢量。 3) u 0, 这就是说如果一个矢量 A 满足 A 0 , 即 A 是一个无旋场,则矢 量 A 可以用一个标量函数的梯度来表示,即 A u 。如静电场中的电场强度就可以用一个 标量函数静电势的梯度来表示。 2. 矢量场的散度 (1) 散度的定义 设有矢量场 A ,在场中任一点 P 处作一个包含 P 点在内的任一闭合曲面 S,S 所限定的

体积为4Ψ,当体积4V以任意方式缩向P点时,取下列极限 41 V 如果上式的极限存在,则称此极限为矢量场A在点P处的散度(divergence),记作 divA=lim 乐aa 4V0 V 在直角坐标系中,散度的表达式 divA= 8A, OA,OA. Ox dy Oz 也可以用哈密顿算子表示,即 7.A= e +, +e. 4e,+4,g+Ae)=4+4+a4 可见,V·A为一标量,表示场中一点处的通量对体积的变化率,也就是在该点处对一 个单位体积来说所穿出的通量,称为该点处源的强度,它描述的是场分量沿着与各自方向上 的变化规律。当又·A的值不为零时,其符号为正或为负。当7·A的值为正时,表示矢量场 A在该点处有散发通量之正源,称为源点:当又·A的值为负时,表示矢量场A在该点处有 吸收通量之负源,称之为汇点:当V·A的值等于零时,则表示矢量场A在该点处无源。我 们称又·A=O的场是连续的或无散的矢量场,在第四章讲的磁场就是连续的或无散的矢量 场。 (2)高斯散度定理 在矢量分析中,一个重要的定理是 7.Ad加=月A 5 上式称为高斯散度定理,它说明了矢量场散度的体积分等于量场在包围该体积的闭合面上 的法向分量沿闭合面的面积分。散度定理广泛地用于将一个封闭面积分变成等价的体积分, 或者将一个体积分变成等价的封闭面积分。有关它的证明这里略去。 3.矢量的环量及旋度 (1)环量的定义 设有矢量场A,1为场中的一条封闭的有向曲线,定义矢量场A环绕闭合路径1的线积 分为该矢量的环量(circulation),记作 r=6A.di 可见,矢量的环量也是一标量,如果矢量的环量不等于零,则在I内必然有产生这种场 的旋涡源:如果矢量的环量等于零,则我们说在I内没有旋涡源
体积为V,当体积V 以任意方式缩向 P 点时,取下列极限 ΔV A dS S ΔV lim0 如果上式的极限存在,则称此极限为矢量场 A 在点 P 处的散度(divergence),记作 ΔV A dS divA S ΔV lim0 在直角坐标系中,散度的表达式 z A y A x A divA x y z 也可以用哈密顿算子表示,即 z A y A x A A e A e A e z e y e x A e z x y x y z x x y y z z 可见, A 为一标量,表示场中一点处的通量对体积的变化率,也就是在该点处对一 个单位体积来说所穿出的通量,称为该点处源的强度,它描述的是场分量沿着与各自方向上 的变化规律。当 A 的值不为零时,其符号为正或为负。当 A 的值为正时,表示矢量场 A 在该点处有散发通量之正源,称为源点;当 A 的值为负时,表示矢量场 A 在该点处有 吸收通量之负源,称之为汇点;当 A 的值等于零时,则表示矢量场 A 在该点处无源。我 们称 A 0 的场是连续的或无散的矢量场,在第四章讲的磁场就是连续的或无散的矢量 场。 (2)高斯散度定理 在矢量分析中,一个重要的定理是 V s AdV A dS 上式称为高斯散度定理,它说明了矢量场散度的体积分等于矢量场在包围该体积的闭合面上 的法向分量沿闭合面的面积分。散度定理广泛地用于将一个封闭面积分变成等价的体积分, 或者将一个体积分变成等价的封闭面积分。有关它的证明这里略去。 3.矢量的环量及旋度 (1)环量的定义 设有矢量场 A ,l 为场中的一条封闭的有向曲线,定义矢量场 A 环绕闭合路径l 的线积 分为该矢量的环量(circulation),记作 L Γ A dl 可见,矢量的环量也是一标量,如果矢量的环量不等于零,则在l 内必然有产生这种场 的旋涡源;如果矢量的环量等于零,则我们说在l 内没有旋涡源

(2)旋度的定义 矢量的环量和矢量穿过闭合面的通量一样都是描绘矢量场A性质的重要物理量,它同 样是一个积分量。为了知道场中每个点上旋祸源的性质,我们引入矢量场的旋度的概念。 设P为矢量场中的任一点,作一个包含P点的微小面元S,其周界为1,它的正向与面 元4S的法向单位矢量万成右手螺旋关系,则矢量场A沿7之正向的环量与面积S之比,当 曲面AS在P点处保持以为法矢的条件下,以任意方式缩向P点,若其极限 A.dl lim S 存在,则称它为矢量场在点P处沿方向的环量面密度(亦即单位面积的环量)。 显然,环量面密度与I所围成的面元S的方向有关。例如,在流体情形中,某点附近 的流体沿着一个面上呈漩涡状流动时,如果I围成的面元与漩涡面的方向重合,则环量面密 度最大:如果所取面元与漩祸面之间有一夹角,得到的环量面密度总是小于最大值:若面元 与漩涡面相垂直,则环量面密度等于零。可见,必存在某一固定矢量B,这个固定矢量B在 任意面元方向上的投影就给出该方向上的环量面密度,B的方向为环量面密度最大的方向, 其模即为最大环量面密度的数值,我们称固定矢量B为矢量A的旋度(curl或rotation),记 作 rotA=B 该式为旋度矢量在方向的投影,即 A.di rot,A 因此,矢量场的旋度仍为矢量。在直角坐标系中,旋度的表达式 aA. rotA 8A,A. (OA,OA. y 也可以用算子又表示,即 @ e V×A=rotA= a 8x ay d2 A A A 一个矢量场的旋度表示该矢量单位面积上的环量, 它描述的是场分量沿着与它相垂直 的方向上的变化规律。若矢量场的旋度不为零,则称该矢量场是有旋的。涡旋流动的水和台 风是流体旋转速度场最好的例子。若矢量场的旋度等于零,则称此矢量场是无旋的或保守的, 静电场中的电场强度就是一个保守场。 旋度的一个重要性质就是它的散度恒等于零,即 7.(7×A=0
(2) 旋度的定义 矢量的环量和矢量穿过闭合面的通量一样都是描绘矢量场 A 性质的重要物理量,它同 样是一个积分量。为了知道场中每个点上旋涡源的性质,我们引入矢量场的旋度的概念。 设 P 为矢量场中的任一点,作一个包含 P 点的微小面元S,其周界为l ,它的正向与面 元S 的法向单位矢量 n 成右手螺旋关系,则矢量场 A 沿l 之正向的环量与面积S 之比,当 曲面S 在 P 点处保持以 n 为法矢的条件下,以任意方式缩向 P 点,若其极限 ΔS A dl l ΔS P lim 存在,则称它为矢量场在点 P 处沿 n 方向的环量面密度(亦即单位面积的环量)。 显然,环量面密度与l 所围成的面元S 的方向有关。例如,在流体情形中,某点附近 的流体沿着一个面上呈漩涡状流动时,如果l 围成的面元与漩涡面的方向重合,则环量面密 度最大;如果所取面元与漩涡面之间有一夹角,得到的环量面密度总是小于最大值;若面元 与漩涡面相垂直,则环量面密度等于零。可见,必存在某一固定矢量 B ,这个固定矢量 B 在 任意面元方向上的投影就给出该方向上的环量面密度,B 的方向为环量面密度最大的方向, 其模即为最大环量面密度的数值,我们称固定矢量 B 为矢量 A 的旋度(curl 或 rotation),记 作 rotA B 该式为旋度矢量在 n 方向的投影,即 rot A ΔS A dl n l ΔS P lim 因此,矢量场的旋度仍为矢量。在直角坐标系中,旋度的表达式 z y x y x z x z y e y A x A e x A z A e z A y A rotA 也可以用算子 表示,即 x y z x y z A A A x y z e e e A rotA 一个矢量场的旋度表示该矢量单位面积上的环量, 它描述的是场分量沿着与它相垂直 的方向上的变化规律。若矢量场的旋度不为零,则称该矢量场是有旋的。涡旋流动的水和台 风是流体旋转速度场最好的例子。若矢量场的旋度等于零,则称此矢量场是无旋的或保守的, 静电场中的电场强度就是一个保守场。 旋度的一个重要性质就是它的散度恒等于零,即 A 0

这就是说,如果有一个矢量场B的散度等于零,则这个矢量就可以用另一个矢量的旋度来表 示,即如果 7.B=0 则可令B=V×A。这里B若表示磁感应强度,则A就是磁矢势。 (3)斯托克斯定理(Stokes'theorem) 矢量分析中另一个重要定理是 手aa=x西 称为斯托克斯定理,其中S是闭合路径1所围成的面积,它的方向与1的方向成右手螺旋关 系,它说明矢量场A的旋度法向分量的面积分等于该矢量沿围绕此面积曲线边界的线积分。 证明略去。 4.一些标量场和矢量场运算的关系式 V (u+v)=Vu+Vv V(u.v)=u(Vv)+(Vu)v V(u2)=2u(7w) 若r=r(x,y,z),p=p(x,y,z),则d0=d.70 若f=f(u),u=(x,y,z),则f=f'(u0Vu 7.(oA=pV·A+A.7o 7.(A×B)=B.(7×A④-A·(7×B) V(A·B)=(A.V)B+(B.V)A+Ax(V×B)+Bx(V×A) V×(A±B)=V×A±V×B V(A±B)=V.A±V.B 7×(pA=pV×A+70×A 7.(7×A=0 7×(V×A=7(V.A-7A 7x×(A×B)=A7.B-BV.A+(B.V)A-(A.V)B ax(V×A=vA2-(a:ya 7.(Vp)=7p V×(7p)=0 vr- V.r=3 V×F=0
这就是说,如果有一个矢量场 B 的散度等于零,则这个矢量就可以用另一个矢量的旋度来表 示,即如果 B 0 则可令 B A 。这里 B 若表示磁感应强度, 则 A 就是磁矢势。 (3)斯托克斯定理(Stokes’ theorem) 矢量分析中另一个重要定理是 A dl A dS l S ( ) 称为斯托克斯定理,其中 S 是闭合路径l 所围成的面积,它的方向与l 的方向成右手螺旋关 系,它说明矢量场 A 的旋度法向分量的面积分等于该矢量沿围绕此面积曲线边界的线积分。 证明略去。 4. 一些标量场和矢量场运算的关系式 (u v) u v (u v) u(v) (u)v u ) 2u(u) ( 2 若 r r(x, y,z),φ φ(x, y,z), 则 dφ dr φ 若 f f (u) , u u(x, y,z) , 则 f f '(u)u φA φ A Aφ ( ) (A B) B ( A) A ( B) 2 ( ) ( ) ( ) ( )0 ( ) A B AB AB A B A A A A A A A A B A B B A B A A B ( ) ( ) ( ) A A A A A ( ) ( ) 2 2 1 2 0 r r r r 3 r 0 ( )( ) ( ) ( ) ( ) AB A B B A A B B A

0)=-月 V×(F1r)=0 Vea)=iaea)(a为常矢量) 5.常用坐标系中的标量场和矢量场运算公式 (1)直角坐标系 Ox 0g,+ V.7oA004. 8o 8o 8o Vo= 72A= 04+04+04】 .A.A. y .+ Ox? 2 e,+ 0r2 02 0z2 (2)柱坐标系 100a,+ roo .a=1o4+la4+4 r or r ad oz a器-(是-器-0} a-4-÷器}-4-4影}月 ,+(VA)e (3)球坐标系 0e,* 器+器影+0器影 70=
3 1/ r r r 3 r r/ 0 ( i ar i ar e iae a 为常矢量) 5. 常用坐标系中的标量场和矢量场运算公式 (1)直角坐标系 x y z eee x y z x y z A A A A x y z z z y y x x x y z A A A A A A A eee yz zx xy 222 2 222 x y z 222 222 222 2 222 2 22 222 xxx yyy zzz x y z AAA AAA AAA A e ee xyz xyz xyz (2)柱坐标系 1 r z e ee rr z 1 1 r z rA A A A rr r z 1 11 z rz r r z A AA A A rA A ee e r z z r rr r 2 2 2 22 2 1 1 r rr r r z 22 2 2 22 22 2 2 r r r r zz A A A A A A e A e Ae rr rr (3)球坐标系 1 1 sin r ee e rr r

-a=1ar4,1asn84),14 rsine a0 rsine do VxA=-1 1a4_ rsine a0 vp器}如 80 r2sin2000 2 72A+ sin 6A, A a0 CAmg 2sin0 sine o +A,+Fsm0la0s 2 +cos0a4- sine do 2sine 四、级数展开和求和 1.二项式级数(1+=1+m+n-r+a-a-2x+… 2 31 2.一维泰勒级数展开 a+for(o+写a++o+ 3.三维泰勒级数展开 e=®w1g人g人 4.常用级数展开 e=1+x x2,x3 +2+3+… *列号号-号 号+号+号+】
2 2 11 1 sin sin sin r r A A A A r rr r 1 11 1 1 sin sin sin r r r A rA A A A rA A e ee r r r r rr 2 2 2 2 2 22 2 11 1 sin sin sin r rr r r r 2 2 2 2 2 2 2 1 - sin sin sin 2 cos sin sin 2sin sin 2 cos sin sin 2sin rr r r r A A A A Ae r A A A A e r A A A A e r 四、级数展开和求和 1.二项式级数 2 3 1 12 1 1 2! 3! n nn nn n x nx x x 2. 一维泰勒级数展开 2 1 (1) (2) ( 1) ( ) 2! 1 ! n x x n f a x f a xf a f a f a n 3. 三维泰勒级数展开 2 3 2! 3! a a a x x fa x fa x f f f 4. 常用级数展开 2 3 1 2! 3! x x x e x 234 ln 1 234 xxx x x 357 1 ln 2 1 357 x xxx x x 246 cos 1 2! 4! 6! xxx x

sinx=x- x3x3 x7 31517I x3,2x317x7 tanx=x+ 315315 sinhx=x+ ++ 十 315174 x2 x4 x5 coshx=1+ 2+41+6 十… 5.常用级数求和 立-a+ 2r-8a+2a+ -a+ 立-0a+2m+(3r+3n-) 1-g+-月 台2i-1357 .111
357 sin 3! 5! 7! xxx x x 35 7 2 17 tan 3 15 315 xx x x x 357 sinh 3! 5! 7! xxx x x 246 cosh 1 2! 4! 6! xxx x 5. 常用级数求和 1 1 2 n i n i n 2 1 12 1 6 n i n inn 2 2 3 1 1 4 n i n i n 4 2 1 12 13 3 1 50 n i n i n n nn 1 1 1 111 1 ln 2 234 i i i 1 1 1 111 1 21 357 4 i i i 2 2 1 1 11 1 1 i i 4 9 16 6