
Chapter 7 Economic Growth Capital and Population
⚫Chapter 7 Economic Growth : ⚫Capital and Population

The lessons ofgrowth theory .can make a positive difference in the lives of hundreds of millions of people. These lessons help us understand why poor countries are poor design policies that can help them grow learn how our own growth rate is affected by shocks and our government's policies
The lessons of growth theory .can make a positive difference in the lives of hundreds of millions of people. These lessons help us • understand why poor countries are poor • design policies that can help them grow • learn how our own growth rate is affected by shocks and our government’s policies

Learning objectives Learn the closed economy Solow model See how a country's standard of living depends on its saving and population growth rates 。Learn how to use the“Golden Rule'” to find the optimal savings rate and capital stock
Learning objectives • Learn the closed economy Solow model • See how a country’s standard of living depends on its saving and population growth rates • Learn how to use the “Golden Rule” to find the optimal savings rate and capital stock

Content 1.Capital Accumulation 1.1 Production Function in Per Worker Term 1.2 Capital Growth and Steady State 1.3 Moving toward the steady state .1.4 Impact of Saving Rate 2.Golden Rule Level of Capital 2.1 Golden Rule Capital Stock 2.2 The transition to the Golden Rule Steady State ·3.Population Growth ·4.Chapter Summary
Content • 1. Capital Accumulation • 1.1 Production Function in Per Worker Term • 1.2 Capital Growth and Steady State • 1.3 Moving toward the steady state • 1.4 Impact of Saving Rate • 2. Golden Rule Level of Capital • 2.1 Golden Rule Capital Stock • 2.2 The transition to the Golden Rule Steady State • 3. Population Growth • 4. Chapter Summary

1.1 The production function In aggregate terms:Y=F(K,L) Define:y=YL=output per worker k=KL capital per worker Assume constant returns to scale: Y=F(zK,zL)for any >0 ·Pick=1L.Then Y/L F(K/L,1) y=F(k,1) y=f(k) where fk)=F(k,1)
1.1 The production function • In aggregate terms: Y = F (K, L ) • Define: y = Y/L = output per worker k = K/L = capital per worker • Assume constant returns to scale: zY = F (zK, zL ) for any z > 0 • Pick z = 1/L. Then Y/L = F (K/L , 1) y = F (k, 1) y = f(k) where f(k) = F (k, 1)
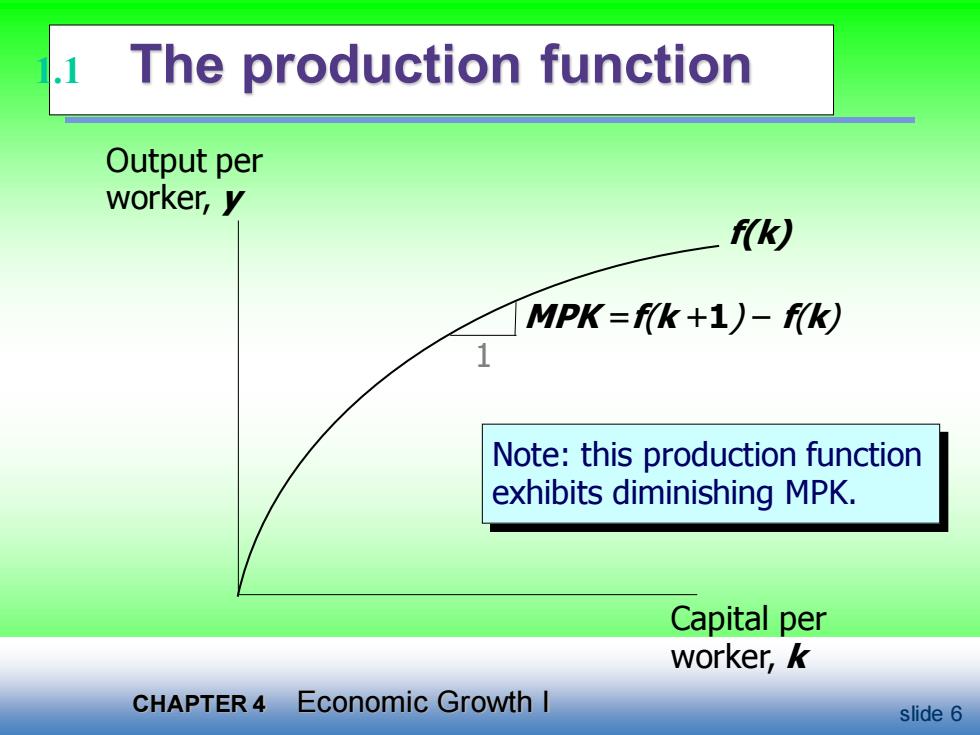
The production function Output per worker,y f(k) MPK=f(k+1)-f(k) Note:this production function exhibits diminishing MPK. Capital per worker,k CHAPTER 4 Economic Growth I slide 6
CHAPTER 4 Economic Growth I slide 6 The production function Output per worker, y Capital per worker, k f(k) Note: this production function exhibits diminishing MPK. 1 MPK =f(k +1) – f(k) 1.1

1.1 The national income identity 。Y=C+I(remember no G) In "per worker"terms: y=c+i where c=CL and i=IL
1.1 The national income identity • Y = C + I (remember, no G ) • In “per worker” terms: y = c + i where c = C/L and i = I/L

1.1 The consumption function 。s=the saving rate, the fraction of income that is saved (s is an exogenous parameter) Note:s is the only lowercase variable that is not equal to its uppercase version divided by L Consumption function:c=(1-s)y (per worker)
1.1 The consumption function • s = the saving rate, the fraction of income that is saved (s is an exogenous parameter) • Note: s is the only lowercase variable that is not equal to its uppercase version divided by L • Consumption function: c = (1–s)y (per worker)

1.2 Saving and investment saving (per worker)=y-c=y -(1-s)y=sy National income identity is y=c+I Rearrange to get:i =y -c =sy (investment saving ! Using the results above, i=sy =sf(k)
1.2 Saving and investment • saving (per worker) = y – c = y – (1–s)y = sy • National income identity is y = c + I Rearrange to get: i = y – c = sy (investment = saving !) • Using the results above, i = sy = sf(k)
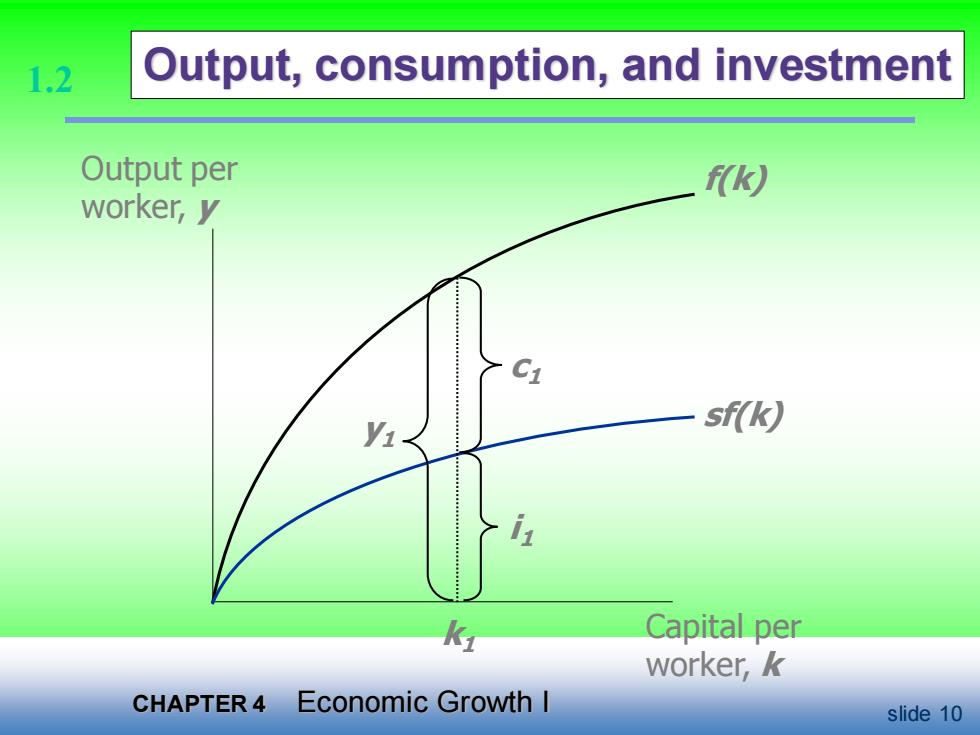
1.2 Output,consumption,and investment Output per f(k) worker,y Ci yi- sf(k) K1 Capital per worker,k CHAPTER 4 Economic Growth I slide 10
CHAPTER 4 Economic Growth I slide 10 Output, consumption, and investment Output per worker, y Capital per worker, k f(k) sf(k) k1 y1 i1 c1 1.2