
華束狮免大学|数学科学学院 School of Mathematical Sciences.East China Normal University 专题选讲 定积分的近似计算 (数值积分) http://math.ecnu.edu.cn/-jypan
http://math.ecnu.edu.cn/~jypan 专题选讲 定积分的近似计算 (数值积分)

为什么数值积分 为什么数值积分 If)=∫fx)dr 数学方法:Newton--Leibniz公式”f(x)dc=F(b)-F(a) ·但是在许多实际计算问题中 )表达式可能比较复杂,计算困难,如)= 1+x6 (2)Fx)难求!甚至有时不能用初等函数表示,如 f(x)= x,f(x)-ex sinx (3):)表达式未知,只有通过测量或实验得来的数据表 http://math.ecnu.edu.cn/~jypan
http://math.ecnu.edu.cn/~jypan 2 为什么数值积分 为什么数值积分 数学方法:Newton-Leibniz 公式 ∫ = − b a f (x)dx F(b) F(a) ( ) ( ) d b a If fx x = ∫ 但是在许多实际计算问题中 (3) f (x) 表达式未知,只有通过测量或实验得来的数据表 (2) F(x) 难求!甚至有时不能用初等函数表示,如 sin 2 ( ) , ( ) x x fx fx e x − = = (1) F(x) 表达式可能比较复杂,计算困难,如 6 1 ( ) 1 f x x = +

数值积分非常重要 数值积分是计算数学的基础和核心,很多连续问题都需要通过数值 积分才能转化为离散问题。 口数值积分内容非常复杂,也非常丰富,特别是弱奇异积分,奇异积 分,超奇异积分,或者被积函数是急剧震荡或急剧衰减的。 口对于高维积分,由于维数效应,计算复杂度往往随维数指数增长, 如何高效地计算高维积分,仍然是计算数学的一大难题。 http://math.ecnu.edu.cn/~jypan 3
http://math.ecnu.edu.cn/~jypan 3 数值积分非常重要 数值积分是计算数学的基础和核心,很多连续问题都需要通过数值 积分才能转化为离散问题。 数值积分内容非常复杂,也非常丰富,特别是弱奇异积分,奇异积 分,超奇异积分,或者被积函数是急剧震荡或急剧衰减的。 对于高维积分,由于维数效应,计算复杂度往往随维数指数增长, 如何高效地计算高维积分,仍然是计算数学的一大难题
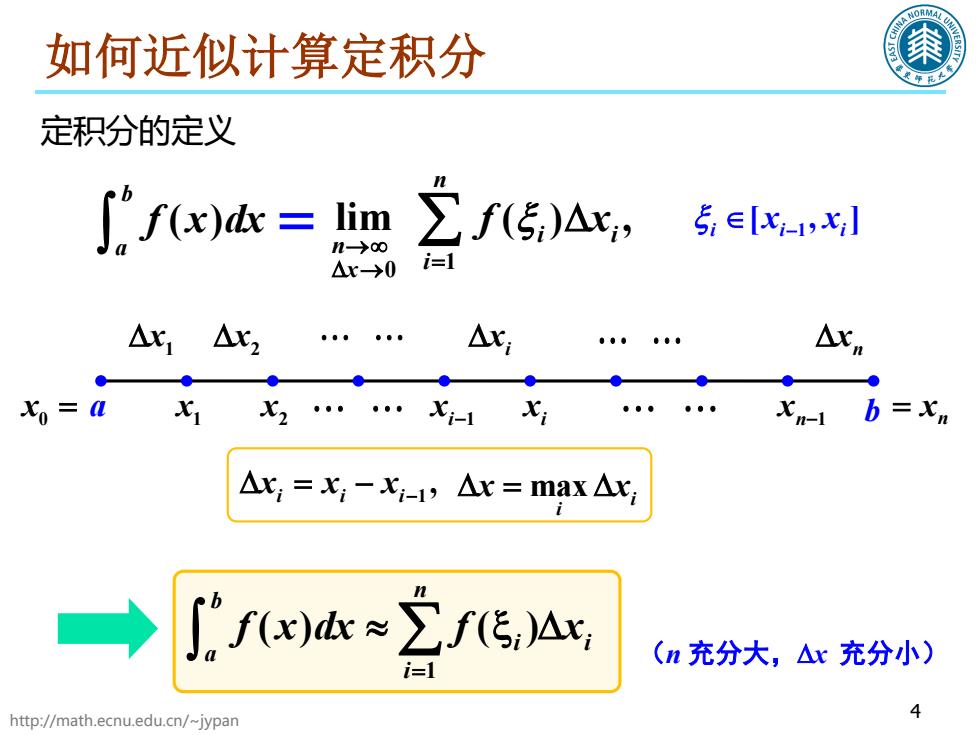
如何近似计算定积分 定积分的定义 ∫心fx)ak=lim ∑fG)Ax,5eK n-→o △x→0 i= △x1 △x2 Axi 1 X=0 2……-1 xn-1 b=xm △r,=x,-x-1,△r=max△c fx)*2f形,Ax (n充分大,△r充分小) 4 http://math.ecnu.edu.cn/~jypan
http://math.ecnu.edu.cn/~jypan 4 ( ) b a f x dx ∫ 1 [ ,] i ii x x ∈ − ξ 0 x = 1 x 2 x n 1 x − n = x 1 ∆x 2 ∆x i 1 x − i ∆x n ∆x () , i i f x ξ ∆ 0 lim n x →∞ ∆ → i x 1 n i= = ∑ 定积分的定义 如何近似计算定积分 1 () ( ) n b i i a i f x dx f x = ∫ ≈ ξ∆ ∑ (n 充分大,∆x 充分小) 1 , i ii x xx ∆= − − max i i ∆= ∆ x x a b

矩形公式 fxf5,Ax 怎么选取:?不同的选取方法 不同的求积方法 矩 fcx)k≈2fxAe 左矩形公式,左点法 i=l 形 公 ∫fx)≈∑fc,A, 右矩形公式,右点法 式 fww2f(色A→ 中炬形公式,中点法 http://math.ecnu.edu.cn/~jypan 5
http://math.ecnu.edu.cn/~jypan 5 矩形公式 怎么选取 𝜉𝜉𝑖𝑖 ?不同的选取方法 不同的求积方法 矩 形 公 式 中矩形公式,中点法 1 () ( ) n b i i a i f x dx f x = ∫ ≈ ξ∆ ∑ 1 1 () ( ) n i i b a i f x dx f x x = ∫ ≈ ∆ ∑ − 1 () ( ) n b i a i i f x xd f x x = ∫ ≈ ∆ ∑ 1 1 2 ( ) i i n b i a i f f x x x dx x = − ≈ ∆ + ∫ ∑ 左矩形公式,左点法 右矩形公式,右点法
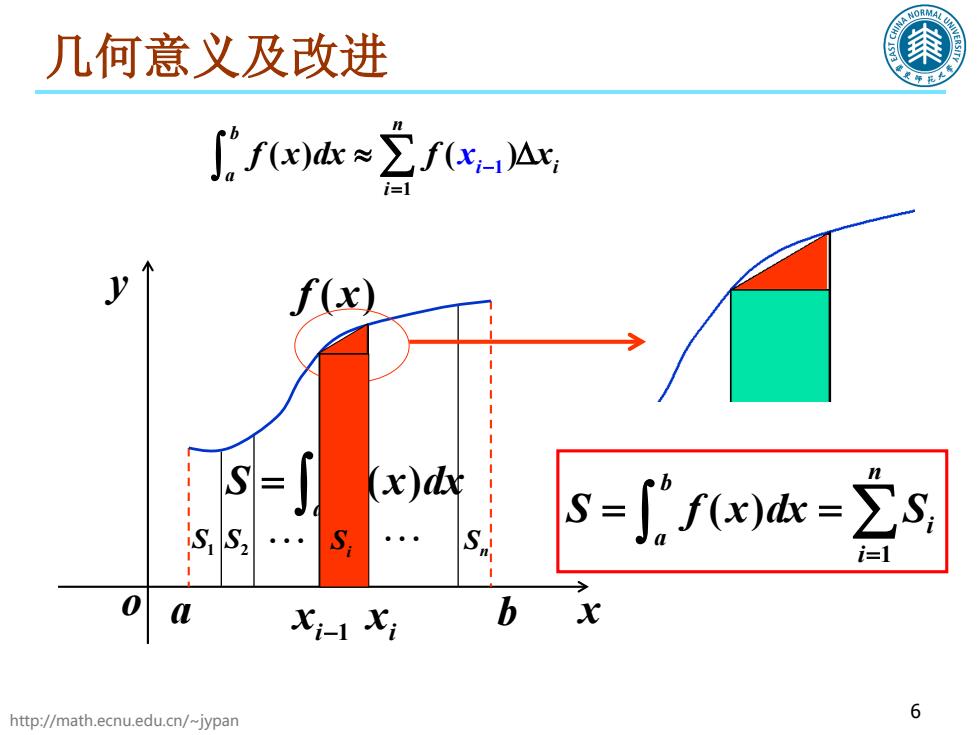
几何意义及改进 ∫fax)k≈2fx4x y f(x) S (x)d S S2 S S=fx)c=∑s i=1 Xi-1Xi http://math.ecnu.edu.cn/~jypan 6
http://math.ecnu.edu.cn/~jypan 6 f x( ) a b i−1 x i x x y o = ∫ ( ) b a S f x dx S1 S2 Si Sn = = = ∫ ∑ 1 ( ) n b i a i S f x dx S 几何意义及改进 1 1 () ( ) n i i b a i f x dx f x x = ∫ ≈ ∆ ∑ −
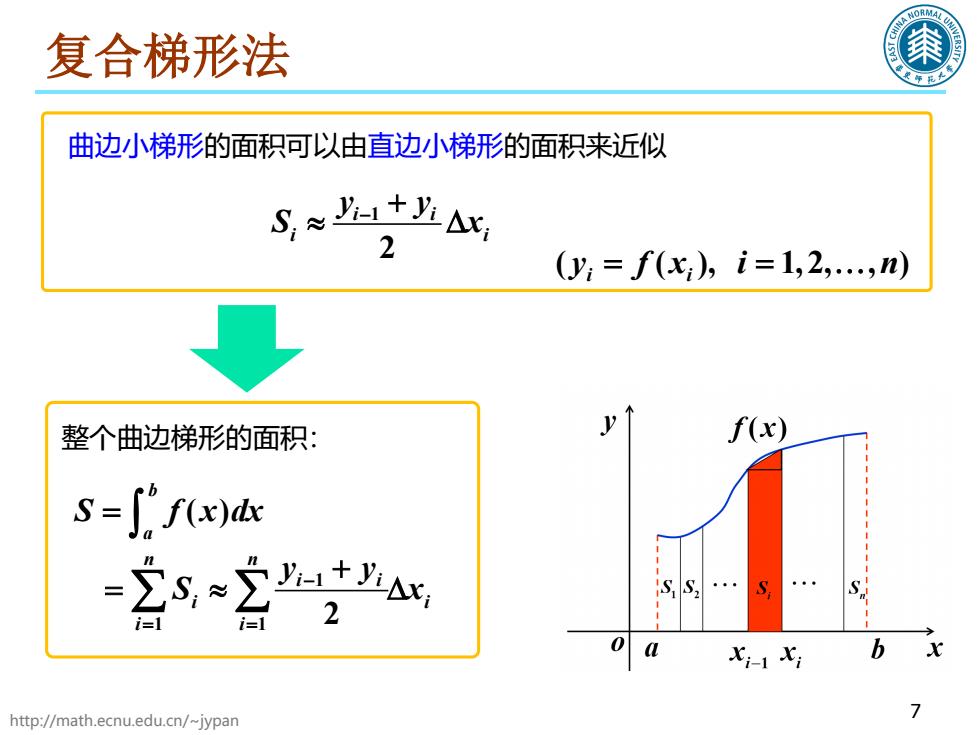
复合梯形法 曲边小梯形的面积可以由直边小梯形的面积来近似 S≈+出Ax 2 (y:=f(x),i=1,2,,n) 整个曲边梯形的面积: f(x) S=∫fx)k ≈,ax S S, i=1 i=1 2 0 b http://math.ecnu.edu.cn/~jypan 7
http://math.ecnu.edu.cn/~jypan 7 1 2 i i i i y y S x − + ≈ ∆ ( ( ), 1, 2, , ) i i y fx i n = = 曲边小梯形的面积可以由直边小梯形的面积来近似 复合梯形法 整个曲边梯形的面积: ( ) b a S f x dx = ∫ 1 1 1 2 n n i i i i i i y y S x − = = + =≈ ∆ ∑ ∑

复合梯形法(续) 如何对积分区间进行分割? 一种简单易用的方法:n等分 A比,=A,=…=Ax,=h=b-0 n s--2容=空 2 A经+月+++分 复合梯形法 http://math.ecnu.edu.cn/~jypan 8
http://math.ecnu.edu.cn/~jypan 8 复合梯形法(续) 如何对积分区间进行分割? 一种简单易用的方法: n 等分 1 2 n ∆ =∆ = =∆ xx x b a h n − = ( ) b a S f x dx = ∫ 1 1 1 1 2 2 1 n n n ii ii i i i i i yy yy S x h − − = = = + + = ≈ ∆= ∑∑ ∑ 0 1 1 ( ) 2 2 b n n a y y f x dx h y y − ≈ +++ + ∫ 复合梯形法

复合抛物线法 f(x) 0 1 b 用抛物线代替该直线,是否会更好? 问题:怎么构造合适的抛物线? http://math.ecnu.edu.cn/~jypan 9
http://math.ecnu.edu.cn/~jypan 9 复合抛物线法 用抛物线代替该直线,是否会更好? 问题:怎么构造合适的抛物线?
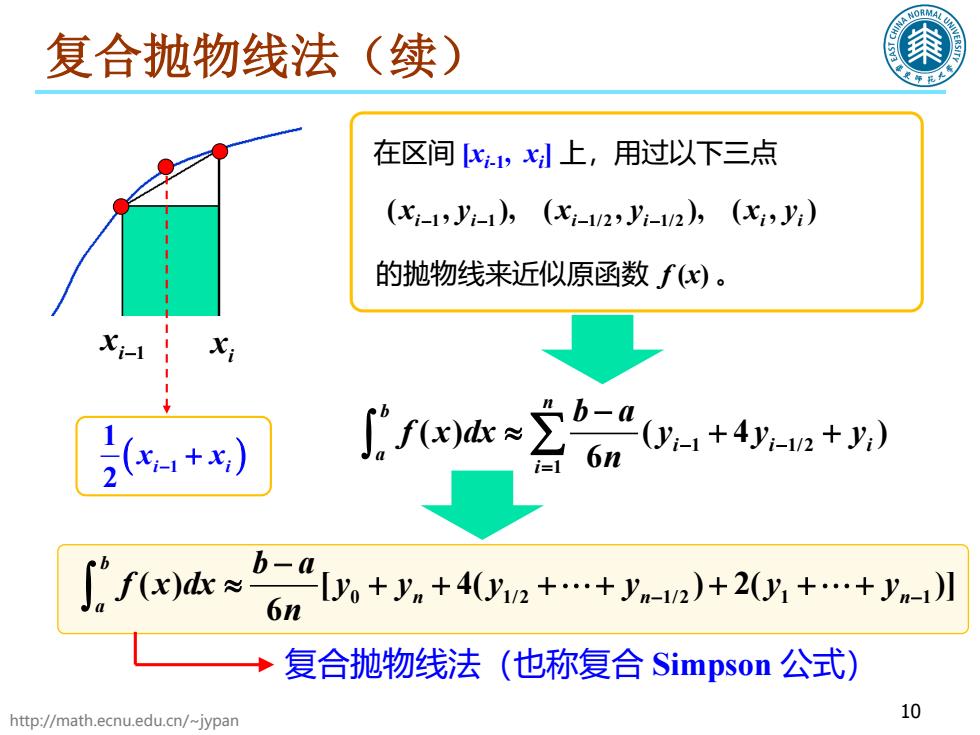
复合抛物线法(续) 在区间x,x上,用过以下三点 (x-1,Jy-1),(-1/2,y-1V2),(,y) 的抛物线来近似原函数f(x)。 Xi-1 (+) ∫fx≈2601+4a+) 16n ifxs ,+y.+4n++ya-n)+2++ya川 6n 复合抛物线法(也称复合Simpson公式) http://math.ecnu.edu.cn/~jypan 10
http://math.ecnu.edu.cn/~jypan 10 复合抛物线法(续) i−1 x i x 在区间 [xi-1, xi ] 上,用过以下三点 1 1 1/2 1/2 ( , ), ( , ), ( , ) i i i i ii x y x y xy −− − − 的抛物线来近似原函数 f (x) 。 ( 1 ) 1 2 i i x x − + 1 1/2 1 ( ) ( 4 ) 6 n b iii a i b a f x dx y y y n − − = − ∫ ≈ ++ ∑ 0 1/2 1/2 1 1 ( ) [ 4( ) 2( )] 6 b nn n a b a f x dx y y y y y y n − − − ≈ + + ++ + ++ ∫ 复合抛物线法(也称复合 Simpson 公式)