
0+语言程序设计 第一讲计算机基础 信息的表示与存储 算法 潘建瑜@MATH.ECNU
1 第一讲 计算机基础 C++ 语言程序设计 潘建瑜@MATH.ECNU —— 信息的表示与存储 —— 算法

7 信息的表示与存储 ▣计算机的数字系统 口常见的进制数及它们之间的转换 ▣原码,反码与补码 ▣非数值信息的表示 http://math.ecnu.edu.cn/-jypan
http://math.ecnu.edu.cn/~jypan 1 信息的表示与存储 计算机的数字系统 常见的进制数及它们之间的转换 原码,反码与补码 非数值信息的表示

计算机信息分类 计算机内部的信息分类 控制信息:指令集,负责软硬件的交互 信息 数值信息:定点数与浮点数 数据信息 非数值信息:字符数据与逻辑数据 信息的存储单位 基本单位:位(bit),字节(Byte=8bit),最小存储单元是字节 ·一个英文字符占一个字节,一个汉字字符占两个字节 http://math.ecnu.edu.cn/~jypan
http://math.ecnu.edu.cn/~jypan 计算机信息分类 信息 控制信息:指令集,负责软硬件的交互 数据信息 数值信息:定点数与浮点数 非数值信息:字符数据与逻辑数据 计算机内部的信息分类 信息的存储单位 ► 基本单位:位(bit),字节(Byte=8bit),最小存储单元是字节 ► 一个英文字符占一个字节,一个汉字字符占两个字节

计算机数字系统 计算机数字系统 计算机采用的是二进制数字系统 基本符号:0、1 -优点:易于物理实现、运算简单、 可靠性高、通用性强 -缺点:可读性差 常用的数制 二进制,八进制,十进制,十六进制 http://math.ecnu.edu.cn/-jypan
http://math.ecnu.edu.cn/~jypan 计算机数字系统 计算机数字系统 计算机采用的是 二进制 数字系统 基本符号:0、1 - 优点:易于物理实现、运算简单、可靠性高、通用性强 - 缺点:可读性差 常用的数制 ► 二进制,八进制,十进制,十六进制

不同进制之间的转换 二进制、八进制、十六进制→十进制 各位数字与它的权相乘,然后相加 例: (101.11)2=1×22+0×21+1×20+1×21+1×22=(5.75)10 (506.2)g=5×82+0×81+6×80+2×81=(326.25)10 (10.C)16=1×161+0×160+12×161=(16.75)10 http://math.ecnu.edu.cn/~jypan
http://math.ecnu.edu.cn/~jypan 不同进制之间的转换 二进制、八进制、十六进制 十进制 各位数字与它的权相乘,然后相加 例: (101.11)2 = 1×22 + 0×21 + 1×20 + 1×2-1 + 1×2-2 = (5.75)10 (506.2)8 = 5×82 + 0×81 + 6×80 + 2×8-1 = (326.25)10 (10.C)16 = 1×161 + 0×160 + 12×16-1 = (16.75)10
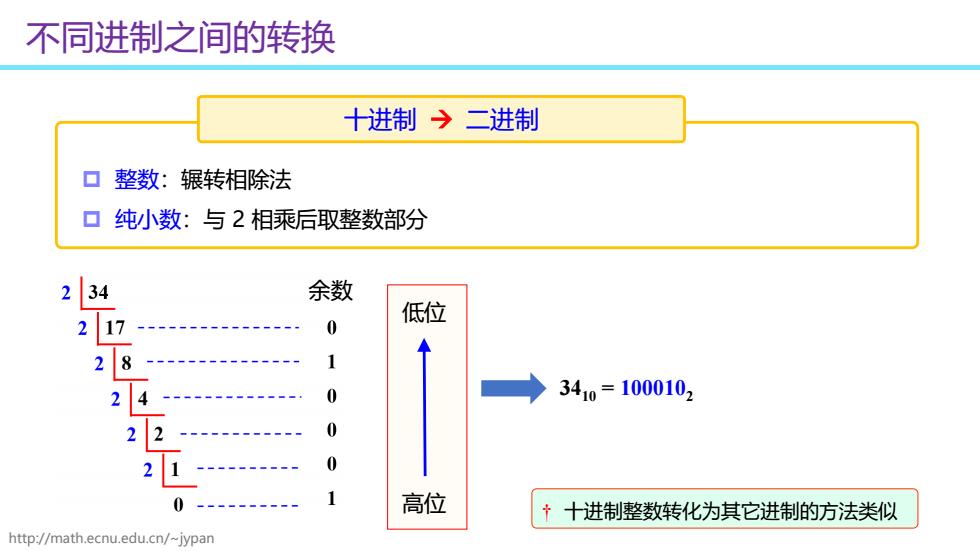
不同进制之间的转换 十进制今二进制 口整数:辗转相除法 口纯小数:与2相乘后取整数部分 2 34 余数 2 0 低位 28 1 2 0 ◆3410=1000102 0 2 1 高位 ↑十进制整数转化为其它进制的方法类似 http://math.ecnu.edu.cn/-jypan
http://math.ecnu.edu.cn/~jypan 不同进制之间的转换 十进制 二进制 整数:辗转相除法 纯小数:与 2 相乘后取整数部分 低位 高位 3410 = 1000102 † 十进制整数转化为其它进制的方法类似 余数

不同进制之间的转换 十进制)二进制 口整数:辗转相除法 口纯小数:与2相乘后取整数部分 0.3125×2=0.625 每次相乘后去掉整数部分,不断乘下去, 0.625×2=1.25 0.312510=0.01012 直到小数部分为0或达到指定的精度为 0.25 ×2=0.5 止,然后取每次相乘后的整数部分即可 0.5 ×2=1.0 绝大部分浮点数无法用二进制精确表示,如0.1,0.2,0.3,… http://math.ecnu.edu.cn/~jypan
http://math.ecnu.edu.cn/~jypan 不同进制之间的转换 十进制 二进制 整数:辗转相除法 纯小数:与 2 相乘后取整数部分 0.3125×2 = 0 . 625 0.625 ×2 = 1 . 25 0.25 ×2 = 0 . 5 0.5 ×2 = 1 . 0 0.312510 = 0.01012 ► 每次相乘后去掉整数部分,不断乘下去, 直到小数部分为 0 或达到指定的精度为 止,然后取每次相乘后的整数部分即可 † 绝大部分浮点数无法用二进制精确表示,如 0.1, 0.2, 0.3,

不同进制之间的转换 八进制、十六进制←→二进制 口每个八进制数对应于一个三位二进制数 口每个十六进制数对应于一个四位二进制数 0分 000 0←→0000 8←>1000 1 分 001 1← 0001 9←分1001 例: 2分 010 2←分0010 A←分1010 11010.102=00011010,10002=1A.816 3←→011 3←→0011 B←分1011 4分 100 4←分0100 C←分1100 5←分101 5←→0101 D分1101 6←分110 6←分0110 E←分1110 7分 111 7←>0111 F←分1111 http://math.ecnu.edu.cn/-jypan
http://math.ecnu.edu.cn/~jypan 不同进制之间的转换 八进制、十六进制 二进制 每个八进制数对应于一个三位二进制数 每个十六进制数对应于一个四位二进制数 0 ↔ 000 1 ↔ 001 2 ↔ 010 3 ↔ 011 4 ↔ 100 5 ↔ 101 6 ↔ 110 7 ↔ 111 0 ↔ 0000 8 ↔ 1000 1 ↔ 0001 9 ↔ 1001 2 ↔ 0010 A ↔ 1010 3 ↔ 0011 B ↔ 1011 4 ↔ 0100 C ↔ 1100 5 ↔ 0101 D ↔ 1101 6 ↔ 0110 E ↔ 1110 7 ↔ 0111 F ↔ 1111 例: 11010.102= 0001 1010 .10002 = 1A.816

原码 数在计算机内部的存储方式 口原码、反码、补码 口二进制数的原码:符号+大小 -符号位:用"0”表示正,用“1”表示负,放在最高位(最左边) 例:用1个字节表示正整数34 34←→00100010 00100010 -34←分10100010 符号位 原码的优点:直观 缺点:(1)四则运算要考虑符号位,规则复杂;(2)零的表示不唯一 http://math.ecnu.edu.cn/~jypan
http://math.ecnu.edu.cn/~jypan 原码 数在计算机内部的存储方式 原码、反码、补码 二进制数的原码:符号 + 大小 - 符号位:用“0”表示正,用“1”表示负,放在最高位(最左边) 0 0 1 0 0 0 1 0 例:用 1 个字节表示正整数 34 符号位 -34 ↔ 10100010 † 原码的优点:直观 † 缺点:(1) 四则运算要考虑符号位,规则复杂;(2) 零的表示不唯一 34 ↔ 00100010

反码与补码 反码与补码 口正数的反码和补码:与原码相同; 口负数的反码:符号位不变,其它位取反(0变1,1变0) 口负数的补码:反码的最末位加1 原码 反码 补码 34←→00100010 ←→00100010 ←>00100010 -34←→10100010 ←分11011101 ←分11011110 计算机以补码方式存放数据 十注1:反码一般不直接使用,通常是作为求补码的中间码 ↑注2:补码的补码就是原码 http://math.ecnu.edu.cn/-jypan
http://math.ecnu.edu.cn/~jypan 反码与补码 反码 与 补码 正数的反码和补码:与原码相同; 负数的反码:符号位不变,其它位取反(0变1,1变0) 负数的补码:反码的最末位加 1 34 ↔ 0 0100010 -34 ↔ 1 0100010 原码 ↔ 0 0100010 ↔ 1 1011101 反码 ↔ 0 0100010 ↔ 1 1011110 补码 计算机以补码方式存放数据 † 注1:反码一般不直接使用,通常是作为求补码的中间码 † 注2:补码的补码就是原码