
附录A应用举例 A1应用:定积分的数值计算 A1.1为什么要数值计算 考虑定积分 I=厂fx)z. A1) 在微积分中,我们可以使用Newton-Leibnit公式来计算,即 f'rGy-ro-r 其中F(工)是被积函数fe)的一个原函数.但是 ·在很多情况下,被积函数的原函数很难求出,或者原函数很复杂,如代句=1十云的原函数为 2+r++C F-a+信(-)+h ·原函数无法用初等函数表示,如 fa)=n,fa=e子,f回=+k和2五 ·在某些实际应用中,被积函数(工)的表达式是未知的,只是通过实验或测量等手段给出了某些离 散点上的值 在这些情况下,我们就需要考虑通过数值方法来计算定积分的近似值,即数值积分 A12定积分数值计算方法 假设定积分心(工)z存在,则根据定积分的定义,我们有 [fer=f6a.6e-A=五--ndr=器A 其中a=20<<2<…<工n-1<n=b是a,创的-个剖分,即 Ar. 为了方便计算,我们不妨对a,进行n等分,即取步长h=,令 x4=a+ih,i=0,1,2.,n. 1
附录 A 应用举例 A.1 应用: 定积分的数值计算 A.1.1 为什么要数值计算 考虑定积分 I = ∫ b a f(x)x. (A.1) 在微积分中, 我们可以使用 NewtonLeibnitz 公式来计算, 即 ∫ b a f(x)x = F(b) − F(a), 其中 F(x) 是被积函数 f(x) 的一个原函数. 但是 • 在很多情况下, 被积函数的原函数很难求出, 或者原函数很复杂, 如 f(x) = 1 1 + x 6 的原函数为 F(x) = 1 3 arctan x + 1 6 arctan ( x − 1 x ) + 1 4 √ 3 ln x 2 + x √ 3 + 1 x 2 − x √ x + 1 + C. • 原函数无法用初等函数表示, 如 f(x) = sin x x , f(x) = e −x 2 , f(x) = √ 1 + k 2 sin2 x. • 在某些实际应用中, 被积函数 f(x) 的表达式是未知的, 只是通过实验或测量等手段给出了某些离 散点上的值. 在这些情况下, 我们就需要考虑通过数值方法来计算定积分的近似值, 即数值积分. A.1.2 定积分数值计算方法 假设定积分 ∫ b a f(x)x 存在, 则根据定积分的定义, 我们有 ∫ b a f(x)x = lim ∆x→0 ∑n i=1 f(ξi)∆xi , ξi ∈ [xi−1, xi ], ∆xi = xi − xi−1, ∆x = max 1≤i≤n ∆xi , 其中 a = x0 < x1 < x2 < · · · < xn−1 < xn = b 是 [a, b] 的一个剖分, 即 为了方便计算, 我们不妨对 [a, b] 进行 n 等分, 即取步长 h = b−a n , 令 xi = a + ih, i = 0, 1, 2, . . . , n. 1

.2 附录A应用举例 于是有 厂fr==e) 因此当n充分大时有 Ir1) (A2) 例A1计算定积分 nl的近似值 思路:将求积区间进行等分,然后在每个小区间中随机选取一个点,不断增大几,直到计算结果满 足精度要求. (exe3_Integral.cpp) #include 4#include #include using namespace std; s const double a =0.0; const double b atan()//b pi/2 545678 srand(time(e)); cout ss left <<setprecision(10); 902 for(int k=0;k<20;k++) h=(b-a)/nj 3456789 for(int return 0; 3} 由定积分的几何意义(曲边梯形的面积,下面的左图剧)可知,上述计算公式A2是在每个小区间上用 矩形的面积来近似曲边梯形的面积(下面的右图),因此称为矩形公式 http://nath.ecnu.edu.cn/-jypan
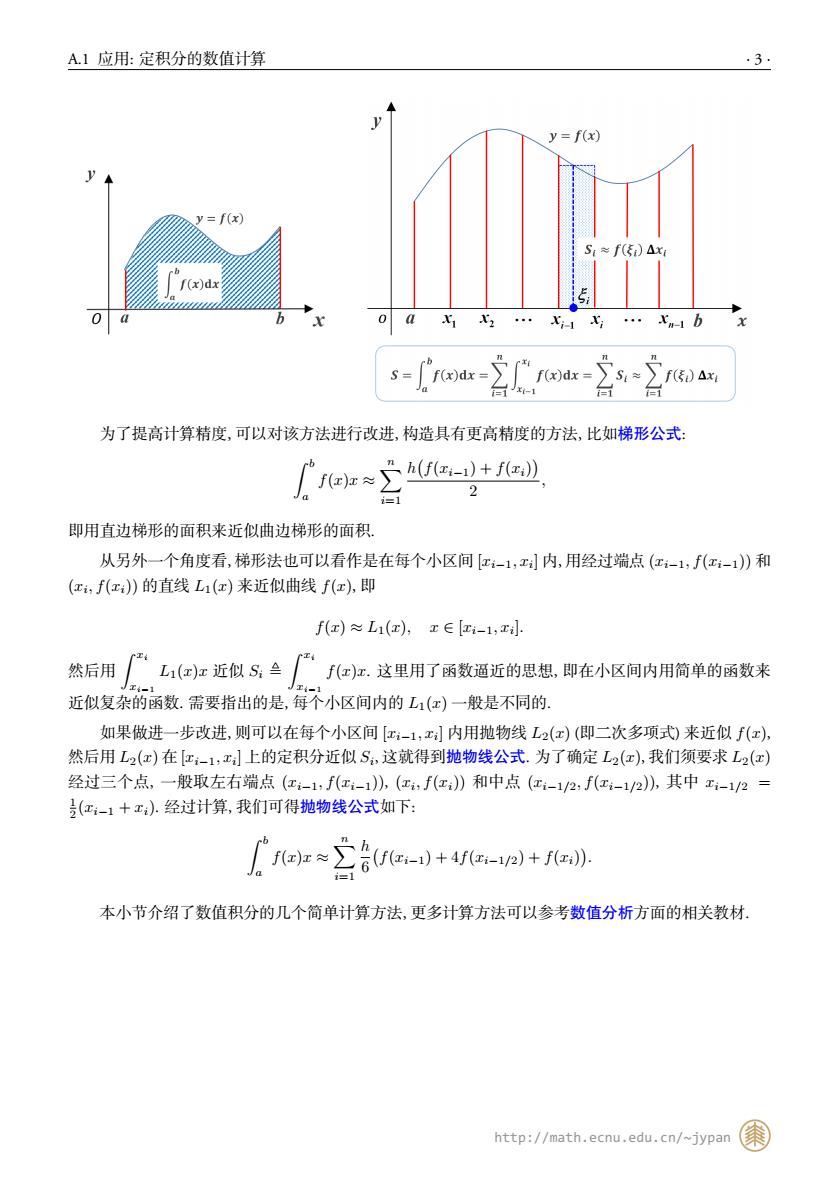
· 2 · 附录 A 应用举例 于是有 ∫ b a f(x)x = lim n→∞ ∑n i=1 hf(ξi). 因此当 n 充分大时有 ∫ b a f(x)x ≈ h ∑n i=1 f(ξi). (A.2) 例 A.1 计算定积分 ∫ π 2 0 sin(x)dx 的近似值. 思路: 将求积区间进行 n 等分, 然后在每个小区间中随机选取一个点 ξi , 不断增大 n, 直到计算结果满 足精度要求. (ex03_Integral.cpp) 1 #include 2 #include 3 #include 4 #include 5 #include 6 using namespace std; 7 8 const double a = 0.0; 9 const double b = atan(1)*2; // b = pi/2 10 11 int main() 12 { 13 long n=1; // 从一等分开始 14 double x, h, S; 15 16 srand(time(0)); 17 cout << fixed << setprecision(10); 18 cout << left; 19 for(int k=0; k<20; k++) 20 { 21 h = (b‐a)/n; 22 S = 0; 23 for(int i=0; i<n; i++) 24 { 25 x = a + h*(i+double(rand())/RAND_MAX); 26 S = S + sin(x); 27 } 28 cout << "n=" << setw(8) << n << " S=" << S*h << endl; 29 n = 2*n; // 不断增大 n 的值 30 } 31 32 return 0; 33 } 由定积分的几何意义 (曲边梯形的面积, 下面的左图) 可知, 上述计算公式 A.2 是在每个小区间上用 矩形的面积来近似曲边梯形的面积 (下面的右图) , 因此称为矩形公式. http://math.ecnu.edu.cn/~jypan
A1应用:定积分的数值计算 3 y=f(x) f(x) f(x)dx s=f)ax=∑fdx=∑s*∑fax i=1x- 为了提高计算精度,可以对该方法进行改进,构造具有更高精度的方法,比如梯形公式: 厂fe*∑bU-)+e 1 即用直边梯形的面积来近似曲边梯形的面积. 从另外一个角度看,梯形法也可以看作是在每个小区间[x-1,x内,用经过端点(亿-1,f(x-1)》和 (红,f()的直线L1(x)来近似曲线f(x),即 f(x)≈L1(x),x∈[x-1,x: 然后用广L1江近似S叁广江.这里用了函数通近的思想即在小区间内用简单的函数来 近似复杂的函数.需要指出的是,每个小区间内的L1(x)一般是不同的. 如果做进一步改进,则可以在每个小区间[z:-1,x]内用抛物线L2(亿)(即二次多项式)来近似f(x), 然后用L2(x)在z;-1,xl上的定积分近似S,这就得到抛物线公式.为了确定L2(r),我们须要求L2(z 经过三个点,一般取左右端点(口-1,f(x-1),(z,f(x)》和中点(红-1/2,f(x-12),其中x-1/2= (红:-1+x).经过计算,我们可得抛物线公式如下 rne+a》 本小节介绍了数值积分的几个简单计算方法,更多计算方法可以参考数值分析方面的相关教材 http:/ath.ecnu,edu,cn/~-jypan®)
A.1 应用: 定积分的数值计算 · 3 · 为了提高计算精度, 可以对该方法进行改进, 构造具有更高精度的方法, 比如梯形公式: ∫ b a f(x)x ≈ ∑n i=1 h ( f(xi−1) + f(xi) ) 2 , 即用直边梯形的面积来近似曲边梯形的面积. 从另外一个角度看, 梯形法也可以看作是在每个小区间 [xi−1, xi ] 内, 用经过端点 (xi−1, f(xi−1)) 和 (xi , f(xi)) 的直线 L1(x) 来近似曲线 f(x), 即 f(x) ≈ L1(x), x ∈ [xi−1, xi ]. 然后用 ∫ xi xi−1 L1(x)x 近似 Si ≜ ∫ xi xi−1 f(x)x. 这里用了函数逼近的思想, 即在小区间内用简单的函数来 近似复杂的函数. 需要指出的是, 每个小区间内的 L1(x) 一般是不同的. 如果做进一步改进, 则可以在每个小区间 [xi−1, xi ] 内用抛物线 L2(x) (即二次多项式) 来近似 f(x), 然后用 L2(x) 在 [xi−1, xi ] 上的定积分近似 Si , 这就得到抛物线公式. 为了确定 L2(x), 我们须要求 L2(x) 经过三个点, 一般取左右端点 (xi−1, f(xi−1)), (xi , f(xi)) 和中点 (xi−1/2, f(xi−1/2)), 其中 xi−1/2 = 1 2 (xi−1 + xi). 经过计算, 我们可得抛物线公式如下: ∫ b a f(x)x ≈ ∑n i=1 h 6 ( f(xi−1) + 4f(xi−1/2) + f(xi) ) . 本小节介绍了数值积分的几个简单计算方法, 更多计算方法可以参考数值分析方面的相关教材. http://math.ecnu.edu.cn/~jypan