
NOBEL PRIS 1915 Sir William Henry Bragg (1862-1942) father Sir William Lawrence Bragg (1890-1871)s son Bragg's Law 1913 SVERIGE WHBRAGG Nobel Prize in Physics 1915 WLBRAGG Diffraction geometry Leyun Wang
Diffraction geometry Sir William Henry Bragg (1862-1942) father Sir William Lawrence Bragg (1890-1871) son Bragg’s Law 1913 Nobel Prize in Physics 1915 Leyun Wang
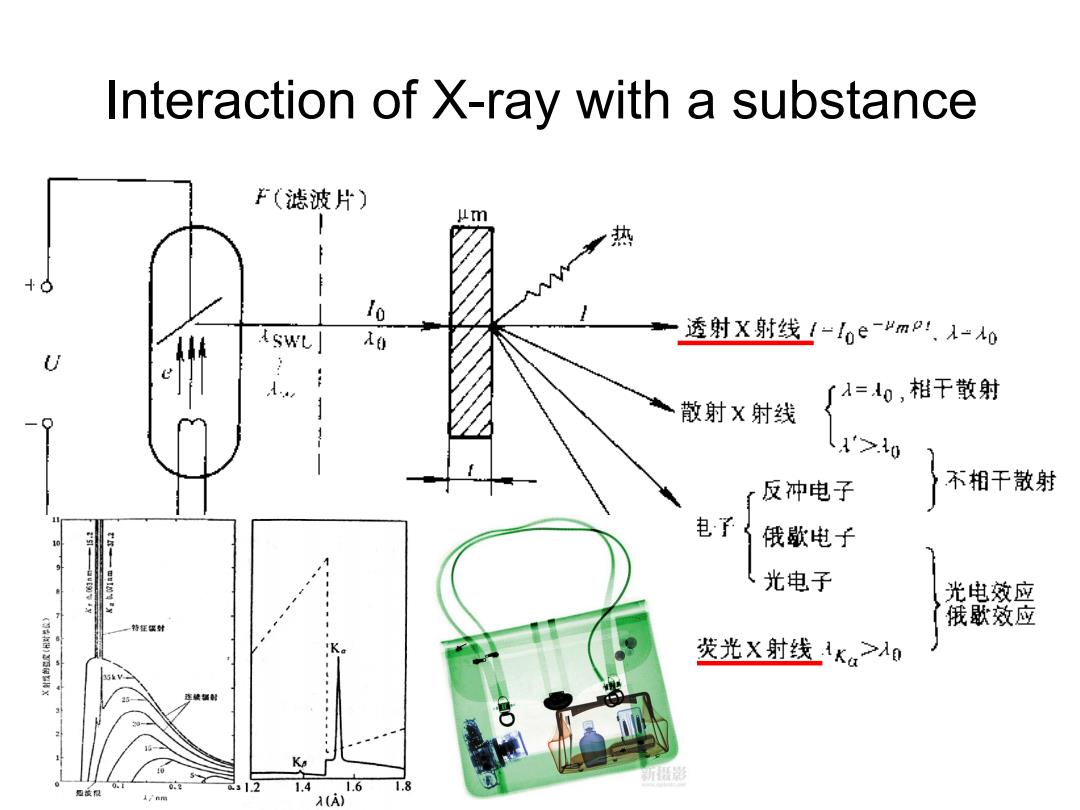
Interaction of X-ray with a substance F(滤波片) 丛m 热 F lo tswL」 入0 透射X射线1-l0e-HmP:,A-o U 「入=0,相干散射 散射X射线 1 1>0 反冲电子 不相干散射 电子{ 10 俄歇电子 光电子 光电效应 俄歌效应 茨光X射线1KaPA0 2 1.6 题藏很 1.4 1/nm A(A)
Interaction of X-ray with a substance
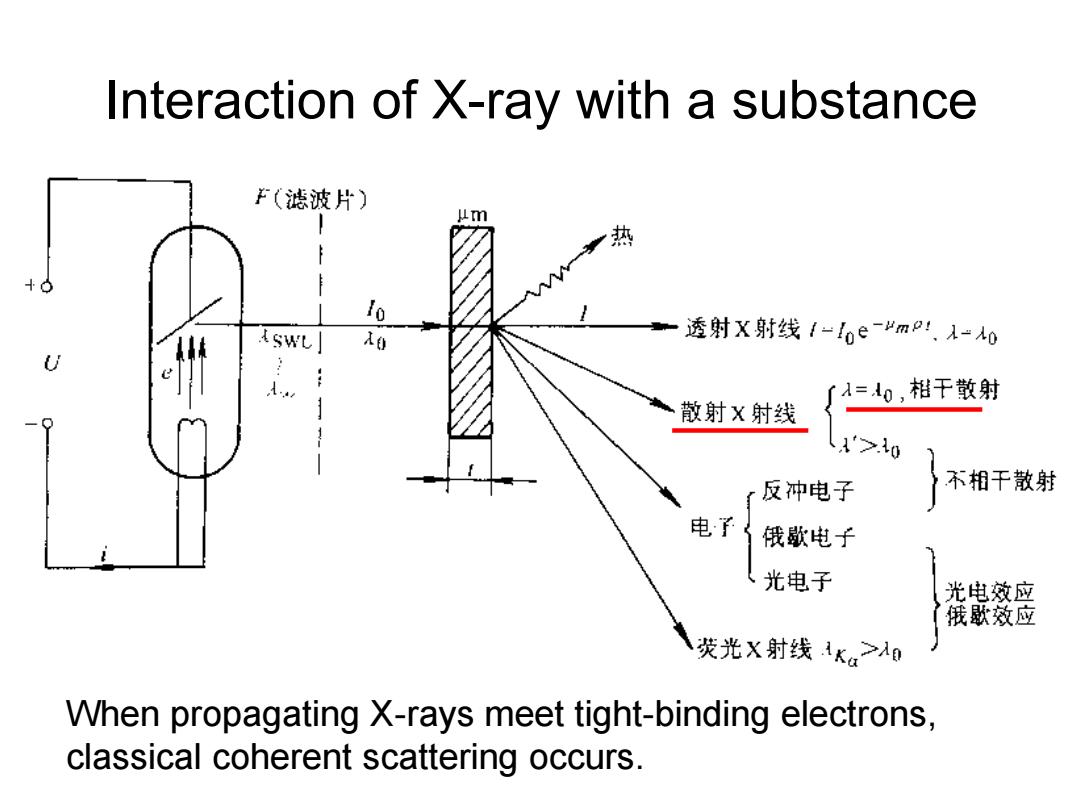
Interaction of X-ray with a substance F(滤波片) 丛m 热 lo tSwL」 Ao 透射X射线1-loe-"mP、A-o U 「入=0,相干散射 散射X射线 1 1'>0 反冲电子 不相干散射 电了{ 俄歇电子 (光电子 光电效应 俄歌效应 荧光X射线1Ka>A日 When propagating X-rays meet tight-binding electrons, classical coherent scattering occurs
Interaction of X-ray with a substance When propagating X-rays meet tight-binding electrons, classical coherent scattering occurs

Diffraction geometry ·Bragg'slaW ·More on Bragg'slaW ·Ewald sphere method Practical X-ray diffraction methods
Diffraction geometry • Bragg’s law • More on Bragg’s law • Ewald sphere method • Practical X-ray diffraction methods
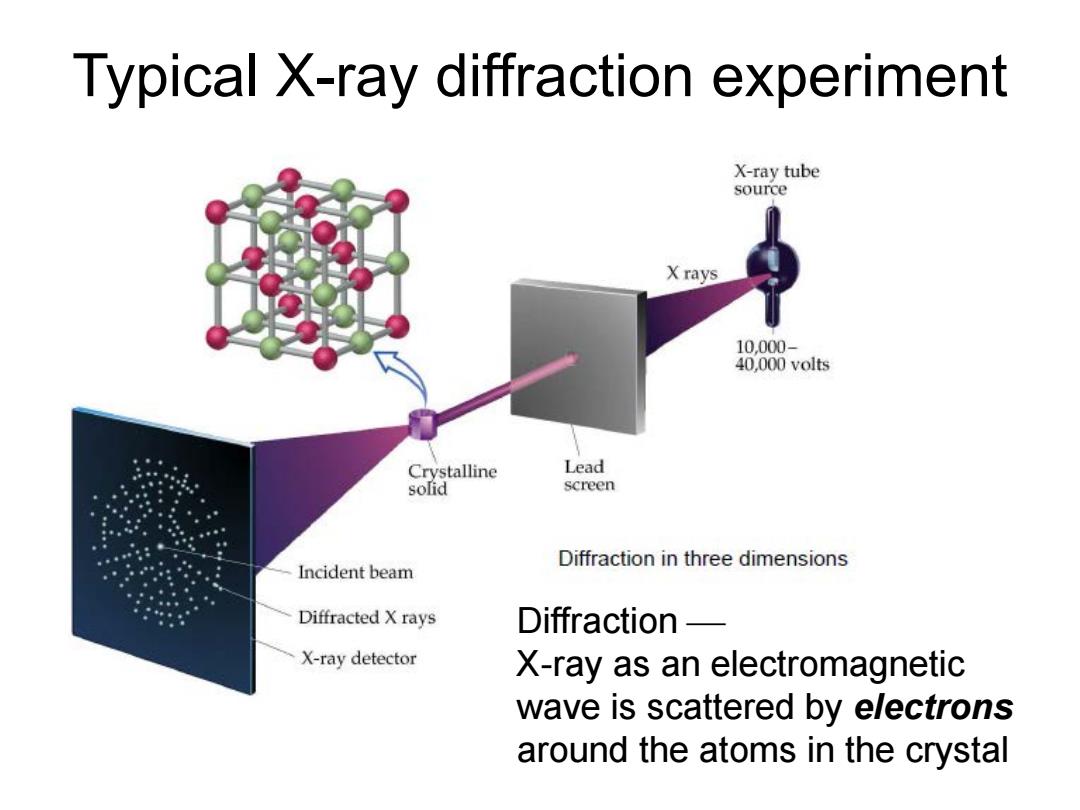
Typical X-ray diffraction experiment X-ray tube source X rays 10.000- 40,000 volts Crystalline Lead solid screen Diffraction in three dimensions Incident beam Diffracted X rays Diffraction X-ray detector X-ray as an electromagnetic wave is scattered by electrons around the atoms in the crystal
Typical X-ray diffraction experiment Diffraction X-ray as an electromagnetic wave is scattered by electrons around the atoms in the crystal
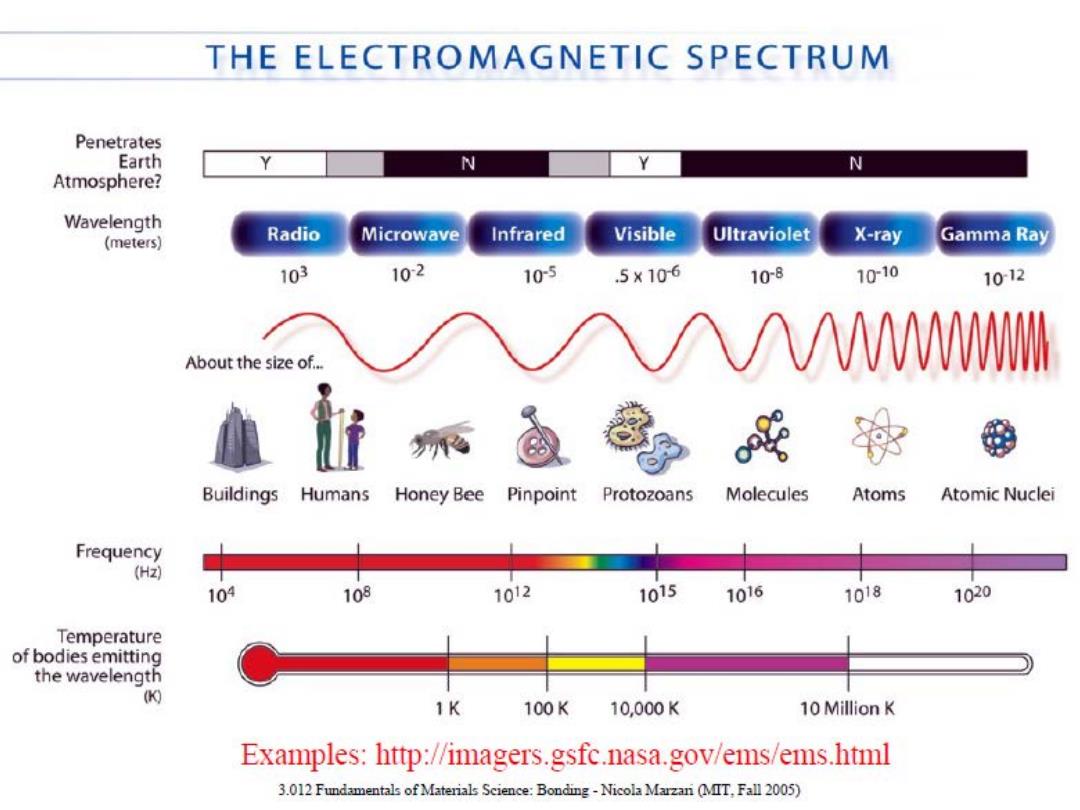
THE ELECTROMAGNETIC SPECTRUM Penetrates Earth N N Atmosphere? Wavelength (meters) Radio Microwave Infrared Visible Ultraviolet X-ray Gamma Ray 103 10-2 105 ,5×106 108 1010 1012 About the size of... A∧WMM Buildings Humans Honey Bee Pinpoint Protozoans Molecules Atoms Atomic Nuclei Frequency (Hz) 104 108 1012 1015 1016 1018 1020 Temperature of bodies emitting the wavelength 0 1K 100K 10,000K 10 Million K Examples:http://imagers.gsfc.nasa.gov/ems/ems.html 3.012 Fundamentals of Materials Science:Bonding-Nicola Marzari (MIT,Fall 2005)

First Laue Equation (AB-CD)=a(cosa,-cosdo)=n, constructive interference: phase difference of two waves n("in-phase") If two in-phase incident waves are deflected by an array of atoms,the deflected waves will not be B in-phase unless their path difference is nA. If the distance between Correlate lattice spacing with X-ray's wavelength. atoms is“a”,then the Laue Fortunately,they are about the same. equation must be satisfied
First Laue Equation constructive interference: phase difference of two waves = nλ (“in-phase”) If two in-phase incident waves are deflected by an array of atoms, the deflected waves will not be in-phase unless their path difference is nλ. If the distance between atoms is “a”, then the Laue equation must be satisfied Correlate lattice spacing with X-ray’s wavelength. Fortunately, they are about the same
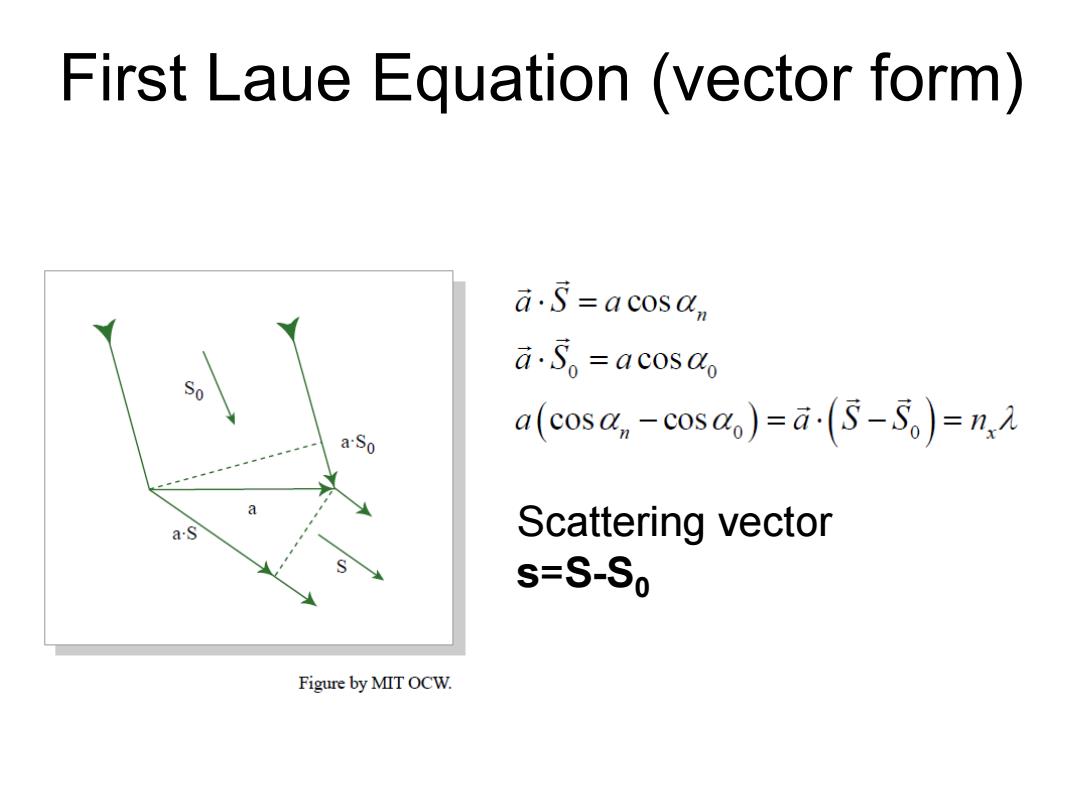
First Laue Equation (vector form) a.S=acosa, a,S。=acos a(cosa,-cosa)=a(S-S)=n,2 a aS Scattering vector s=S-So Figure by MIT OCW
First Laue Equation (vector form) Scattering vector s=S-S0
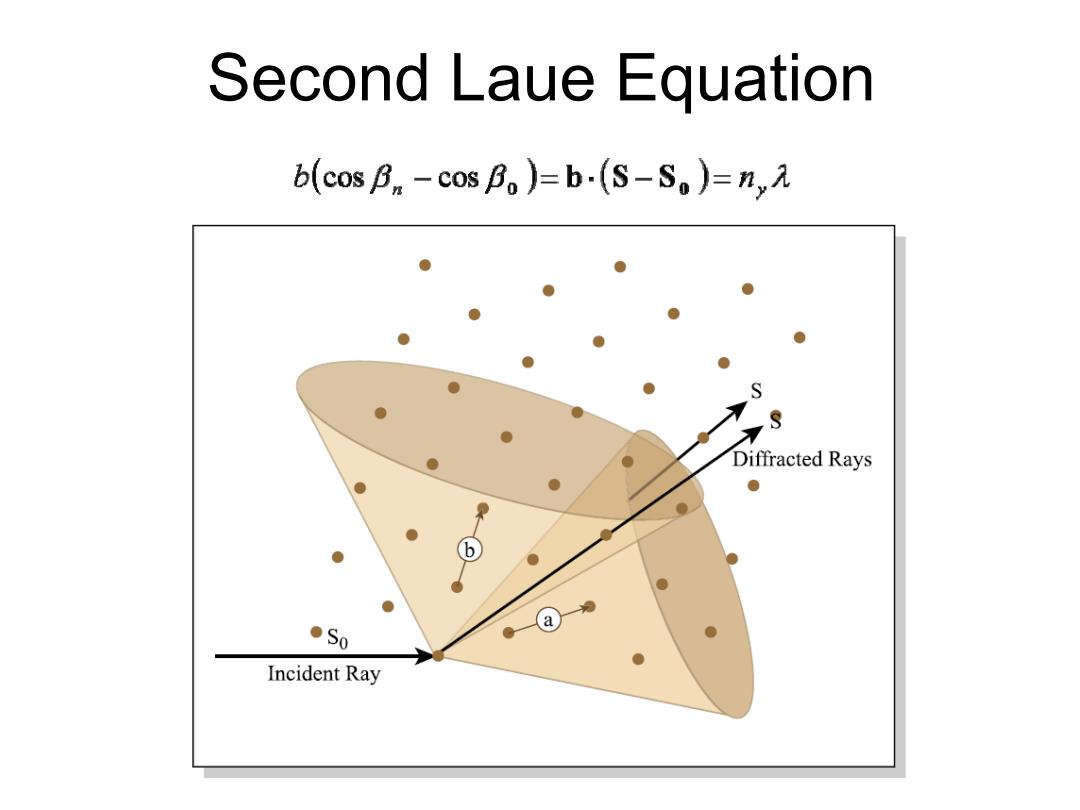
Second Laue Equation b(cos B,-cosBo)=b.(S-S.)=n, s Diffracted Rays ●S0 Incident Ray
Second Laue Equation

Third Laue Equation a(cOS-cosa)=a.(S-S,)=n,元 b(Cos B-cosf)=b(S-S。)=2, c(cosyn-cosY。)=c.(S-S,)=n
Third Laue Equation