http://www.periodictable.com/Properties/A/LatticeConstants.sp.wt.html Precise lattice parameter determination 80 60 40 20 0 20 40 60 80 100 Atomic Number
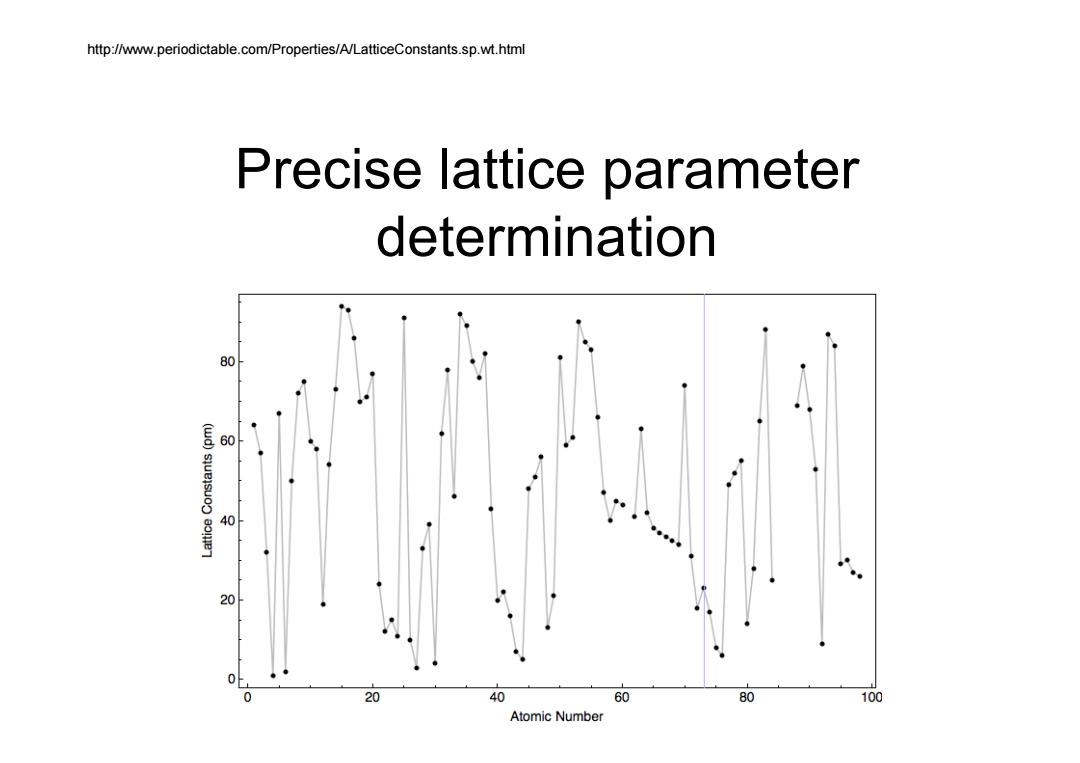
Precise lattice parameter determination http://www.periodictable.com/Properties/A/LatticeConstants.sp.wt.html

Lattice parameter matters in: 1.thermal expansion coefficient 2.residual stress measurement 3.study phase transformation 4.substitution vs interstitial solid solution
Lattice parameter matters in : 1. thermal expansion coefficient 2. residual stress measurement 3. study phase transformation 4. substitution vs interstitial solid solution ……
Using lattice parameter change to identify phase transformation in NigAl Experiment data -sum of peak 1 and peak 2 二 peak 1-y' peak 2-y 分峰条件: 峰形Voigt Accelerating Voltage Camera Length Magnificatior 200kV 10000x 500nm 置信度99% 采集条件: Misfit:0.15~0.35% 0.01/step 4s/step 72 73 74 75 76 77 78 20
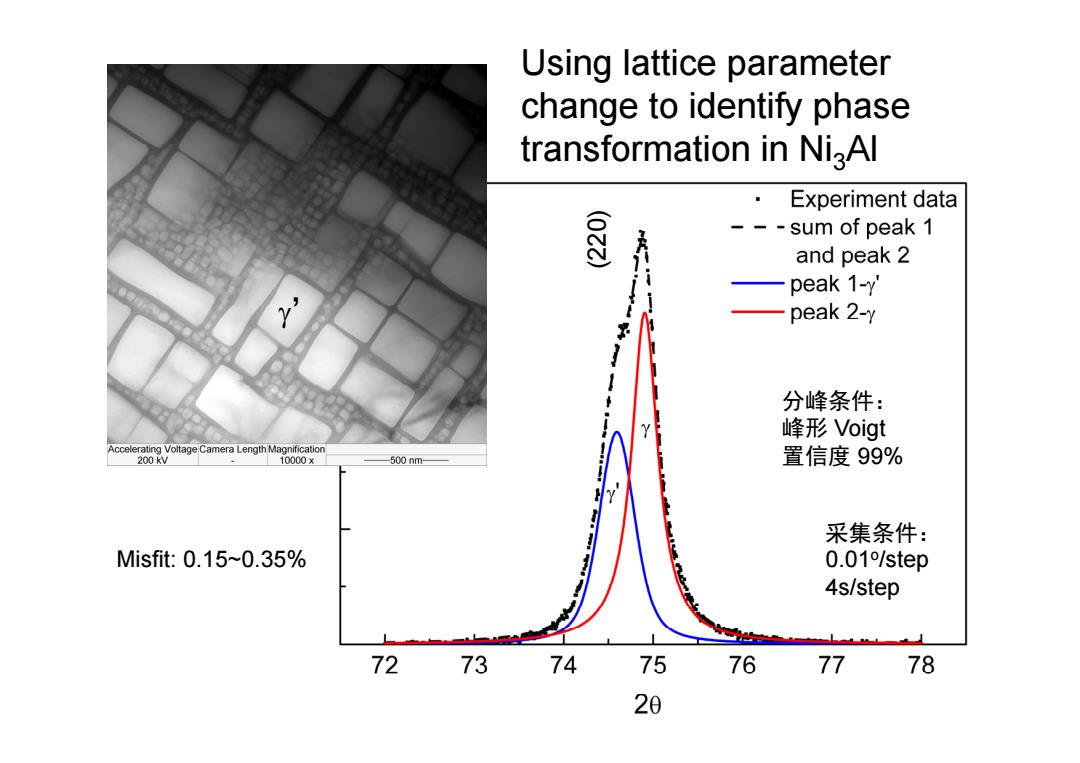
’ 采集条件: 0.01o/step 4s/step 分峰条件: 峰形 Voigt 置信度 99% Using lattice parameter change to identify phase transformation in Ni3Al Misfit: 0.15~0.35% (220)
Identify the thermal expansion coefficient from in situ high-T XRD-TisSig 2242 (3251) An accuracy of at least 0.06%is required. Asuejul 200 *L.T.Zhang and J.S.Wu,Scripta 400 59 Temperature Materialia,38(1998)307 60 600 0.755 61 800 28 64 TigSia 65 1000 66 0750 0.525 0.745 0.520 ● 0.740 ● 0.515 ● a-axis ●c-ais 0.735 0.510 0 200 400 600 800 1000 200 400 600 800 1000 Temperature(C) Temperature(c)
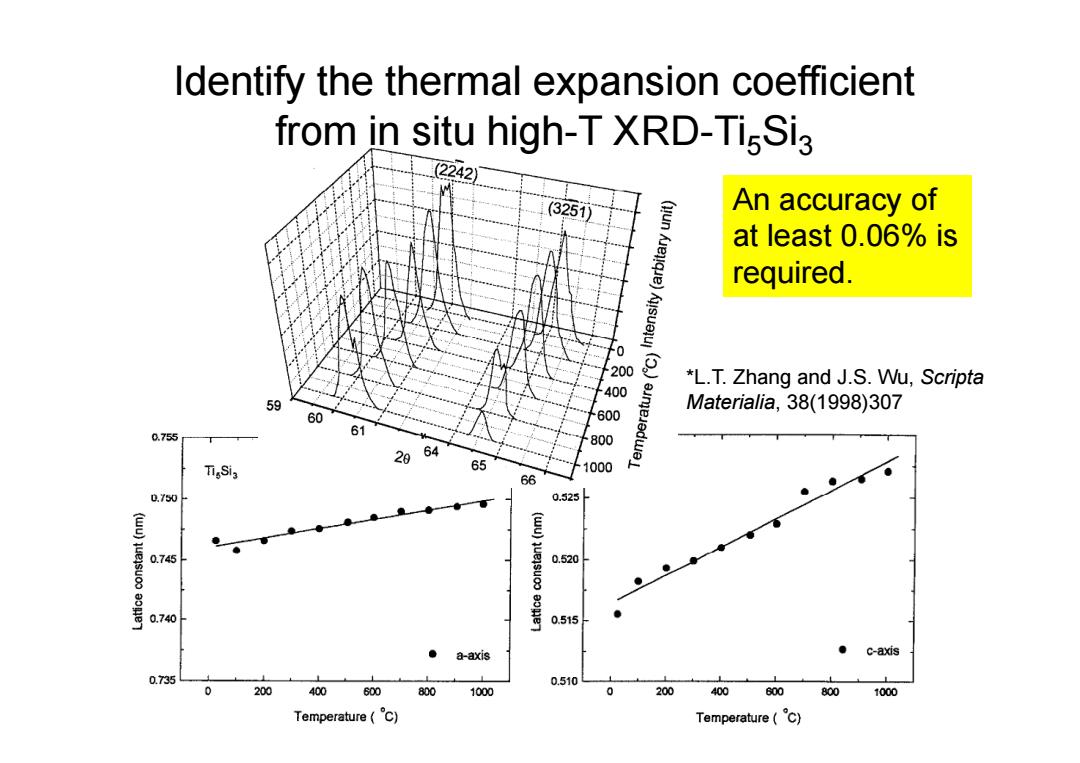
*L.T. Zhang and J.S. Wu, Scripta Materialia, 38(1998)307 Identify the thermal expansion coefficient from in situ high-T XRD-Ti5Si3 An accuracy of at least 0.06% is required
(110 Strongest 3 peaks Si no.peak 2Theta d I/I1 FWHM no. (deg) (A) (deg) 28.3699 3.14332 100 0.11470 2 2 47.2380 1.92256 55 0.10980 56.0600 1.63912 6 0.10770 4000 Peak Data List peak 2Theta d I/I1 FWHM no. (deg) (A) (deg) 义 28.3699 3,14332 100 0.11470 23 47.2380 1.92256 55 0.10980 56.0600 1.63912 36 0.10770 4 69.0791 1.35858 8 0.11400 56 76.3222 1.24666 14 0.11000 E 87.9814 1.10905 17 0.12150 7 94.9030 1.04557 0.12970 2000 106.6626 0.96033 5 0.15280 18 114.0568 0.91816 10 0.14960 127.5153 0.85879 8 0.17250 1 136.8696 0.82826 4 0.18340 (400 3311) (61) 120
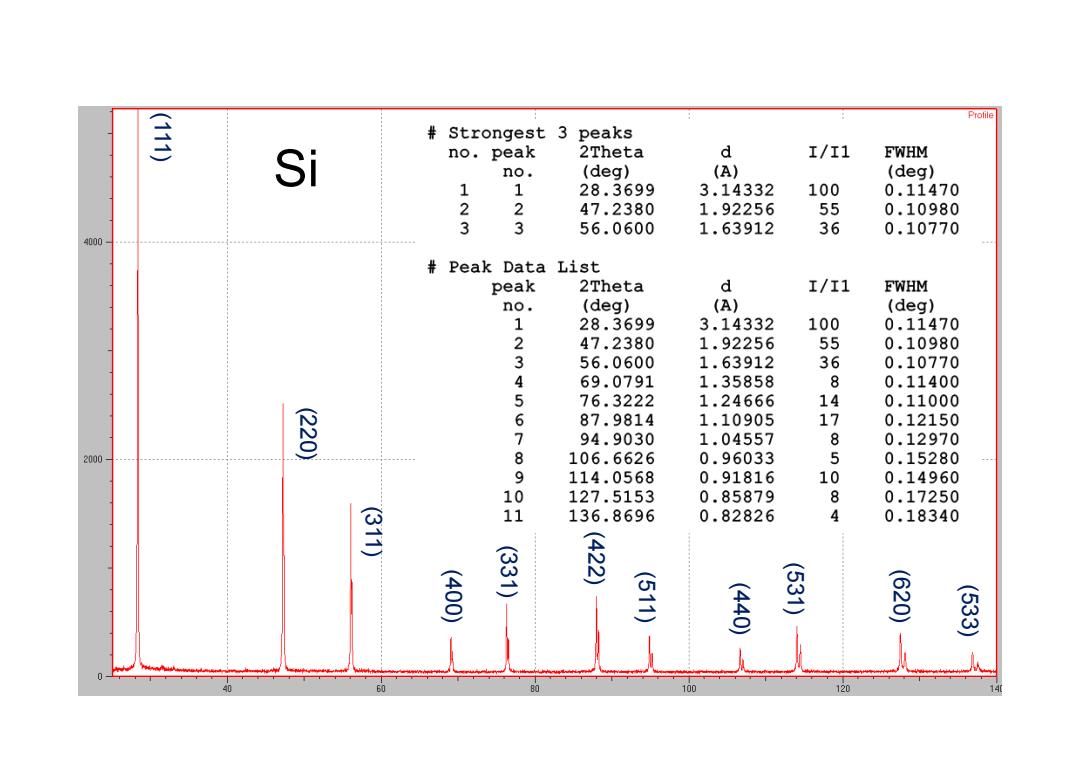
(111) (220) (311) (400) (331) (422) (511) (440) (531) (620) (533) Si
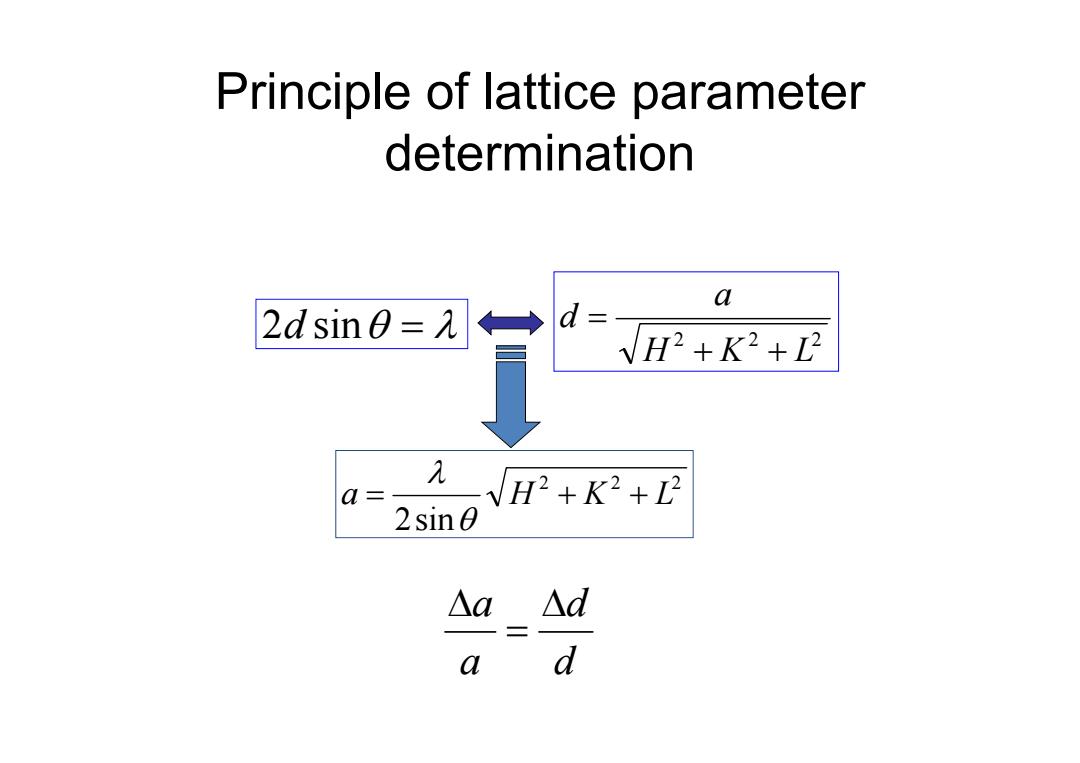
Principle of lattice parameter determination a 2dsin0=元 d= VH2+K2+D 几 a= VH2+K2+2 2sine △a △d a d
Principle of lattice parameter determination 2 2 2 2sin a H K L 2 d sin 2 2 2 H K L a d d d a a

The error in peak position determination 九 d 2sin 0 △兄 λ△0cosB △d= 2sin0 2sin20 △d △元△0cos0 d 元 sinθ
The error in peak position determination 2 2sin cos 2sin d 2sin d sin cos d d
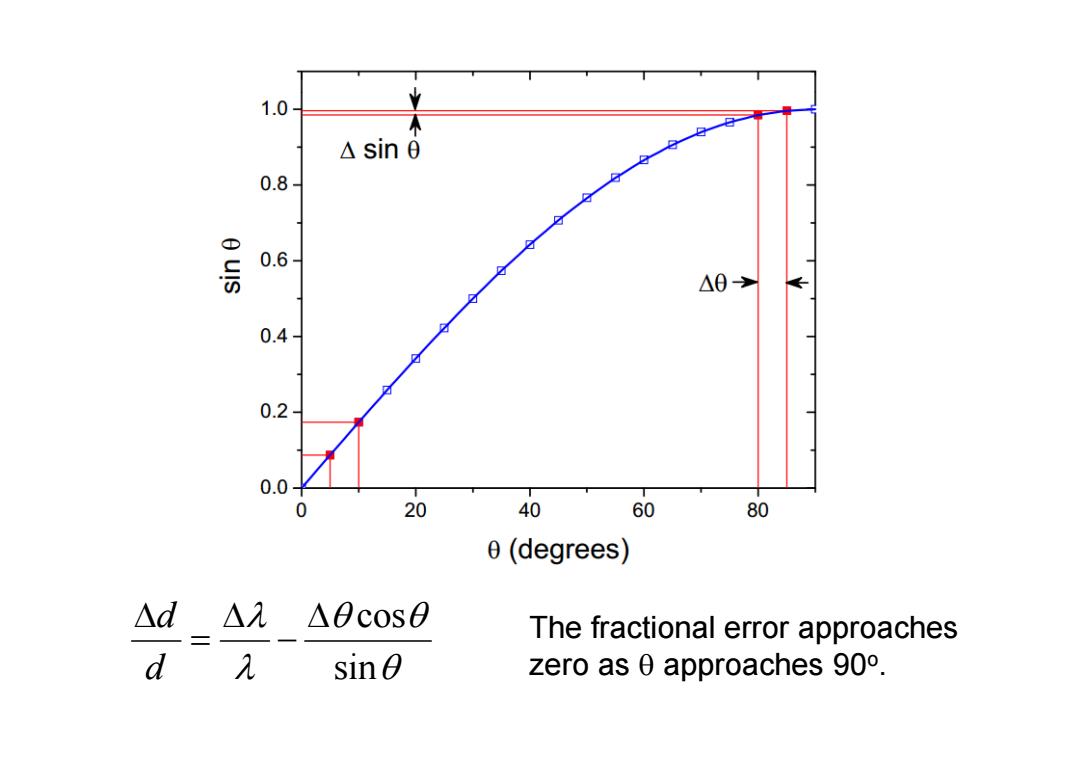
1.0 业 不 △sin0 0.8 0 uls 0.6 △0→ 0.4- 0.2- 0.0 0 20 40 60 80 0(degrees) △d △元 △0cos0 The fractional error approaches d λ sinO zero as 0 approaches 90o
sin cos d d The fractional error approaches zero as approaches 90 o

Use peaks with large 20 0.030 0.025 0.05°-9 0.01°-A9 8 0.020 0.015 0.005°-9 p/pV 0.010 0.005 0.001°-A9 0.000 30405060708090 0() 点阵参数测量精度与和△的关系
30 40 50 60 70 80 90 0.000 0.005 0.010 0.015 0.020 0.025 0.030 d/d , % 0.010 ~ 0.050 ~ 0.0050 ~ 0.0010 ~ 点阵参数测量精度与 θ 和Δθ的关系 Use peaks with large 2

The key to high precision in parameter measurements lies in the use of back reflected beams having 20 values as near to 180 as possible! It is impossible to reach 180!