
第2章逻辑代数基础
第2章 逻辑代数基础

第四节 逻辑函数及其表示方法 逻辑函数的定义: 设某一逻辑电路中的输入逻辑变量为A,B,C, 输出逻辑变量为L,如果当A,B,C,的值确定后, L的值就唯一地被确定下来,那么L就称为A,B,C, 的逻辑函数。记为L=L(A,B,C
逻辑函数的定义: 设某一逻辑电路中的输入逻辑变量为A,B,C,., 输出逻辑变量为L,如果当 A,B,C,.,的值确定后, L的值就唯一地被确定下来,那么L就称为A,B,C,., 的逻辑函数。记为L=L(A,B,C,.) 。 第四节 逻辑函数及其表示方法

在解决某一实际问题时,我们经常要研究因变量和自变 量的逻辑关系问题,即需要建立逻辑函数。 建立逻辑函数的步骤大致可分为: 1、分析逻辑命题,确定逻辑变量和逻辑函数。 2、研究逻辑变量和逻辑函数间的因果关系,列出其真 值表。 3、根据真值表写出逻辑函数表达式:
在解决某一实际问题时,我们经常要研究因变量和自变 量的逻辑关系问题,即需要建立逻辑函数。 建立逻辑函数的步骤大致可分为: 1、分析逻辑命题,确定逻辑变量和逻辑函数。 2、研究逻辑变量和逻辑函数间的因果关系,列出其真 值表。 3、根据真值表写出逻辑函数表达式

2.4.1逻辑函数的建立 一、逻辑函数的建立 例,分析一个控制楼梯照明灯的电路。其单刀双掷开 关A装在楼下,B装在楼上,从而实现楼上开灯,楼下 关灯,反之亦然。 1、依题意,确定开关A,B为逻辑变量,灯F为逻辑 函数。并设开关A,B上合为0,下合为1,灯F亮为1, 灭为0。 2、列出真值表。 3、写出逻辑函数式:F=A~B+AB
1、依题意,确定开关A,B为逻辑变量,灯F为逻辑 函数。并设开关A,B上合为0,下合为1,灯F亮为1, 灭为0。 2、列出真值表。 例,分析一个控制楼梯照明灯的电路。其单刀双掷开 关A装在楼下,B装在楼上,从而实现楼上开灯,楼下 关灯,反之亦然。 2.4.1 逻辑函数的建立 一、逻辑函数的建立
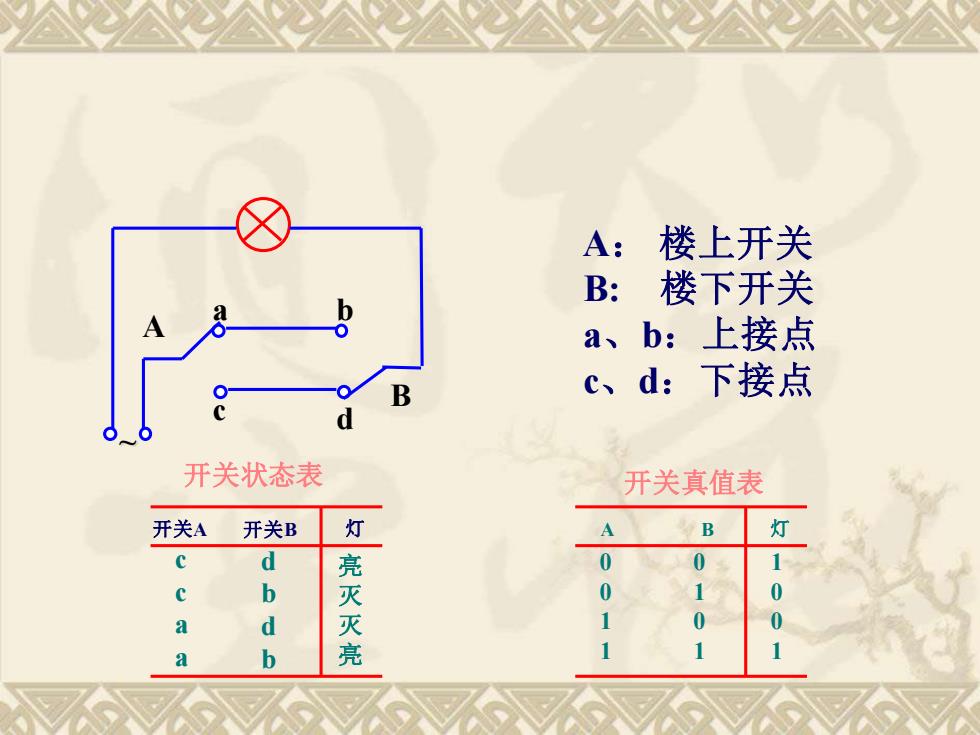
A:楼上开关 B: 楼下开关 a、b:上接点 B c、d: 下接点 开关状态表 开关真值表 开关A 开关B 灯 A B 灯 d 亮 0 0 b 0 0 a d a b 亮
~ A B a b c d A : 楼上开关 B: 楼下开关 a、b:上接点 c、d:下接点 A B 灯 0011 0101 1001 开关 A 开关 B 灯 ccaa 亮灭灭亮 dbdb 开关状态表 开关真值表

÷二、逻辑函数的表示方法 ⑧1、真值表(便于直观的观看变量与函数之间的 关系)。 2、逻辑表达式:表达逻辑函数的输入与输出关 系的与、或、非等逻辑运算的组合式。 3、逻辑图:将逻辑函数式中各变量之间的与、 或、非等运算关系用相应的逻辑符号表示出来, 即画出能表示函数关系的逻辑图
❖ 二、逻辑函数的表示方法 1、真值表(便于直观的观看变量与函数之间的 关系)。 2、逻辑表达式:表达逻辑函数的输入与输出关 系的与、或、非等逻辑运算的组合式。 3、逻辑图:将逻辑函数式中各变量之间的与、 或、非等运算关系用相应的逻辑符号表示出来, 即画出能表示函数关系的逻辑图
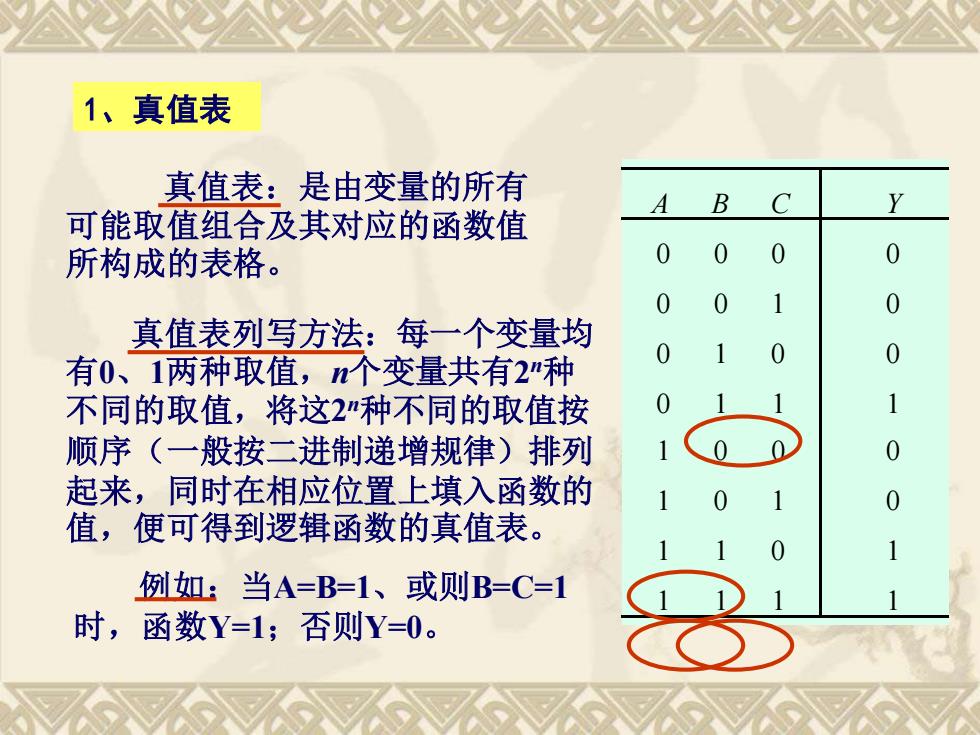
1、真值表 真值表:是由变量的所有 A B C 可能取值组合及其对应的函数值 所构成的表格。 0 0 0 0 0 0 0 真值表列写方法:每一个变量均 有0、1两种取值,个变量共有2种 0 不同的取值,将这2"种不同的取值按 顺序(一般按二进制递增规律)排列 起来,同时在相应位置上填入函数的 值,便可得到逻辑函数的真值表。 例如:当A=B=1、或则B=C=1 时,函数Y=1;否则Y=0
1、真值表 真值表:是由变量的所有 可能取值组合及其对应的函数值 所构成的表格。 真值表列写方法:每一个变量均 有0、1两种取值,n个变量共有2 n种 不同的取值,将这2 n种不同的取值按 顺序(一般按二进制递增规律)排列 起来,同时在相应位置上填入函数的 值,便可得到逻辑函数的真值表。 A B C Y 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 0 0 1 0 0 1 例如:当 1 A=B=1、或则B=C=1 时,函数Y=1;否则Y=0

2、逻辑表达式 3、卡诺图 逻辑表达式:是由 卡诺图:是由表示变量的所有 逻辑变量和与、或、非3 可能取值组合的小方格所构成的图 种运算符连接起来所构成 形。 的式子。 逻辑函数卡诺图的填写方法: 在那些使函数值为1的变量取值组 函数的标准与或表达 合所对应的小方格内填入1,其余 式的列写方法:将函数的 的方格内填入0,便得到该函数的 真值表中那些使函数值为 卡诺图。 1的最小项相加,便得到 函数的标准与或表达式。 Y=ABC+ABC ABC 00 01 10 0 0 0 =∑m(3,6,7)
2、逻辑表达式 逻辑表达式:是由 逻辑变量和与、或、非3 种运算符连接起来所构成 的式子。 函数的标准与或表达 式的列写方法:将函数的 真值表中那些使函数值为 1的最小项相加,便得到 函数的标准与或表达式。 = = + + m(3,6,7) Y ABC ABC ABC 3、卡诺图 卡诺图:是由表示变量的所有 可能取值组合的小方格所构成的图 形。 逻辑函数卡诺图的填写方法: 在那些使函数值为1的变量取值组 合所对应的小方格内填入1,其余 的方格内填入0,便得到该函数的 卡诺图。 AB C 00 01 11 10 0 0 0 1 0 1 0 1 1 0
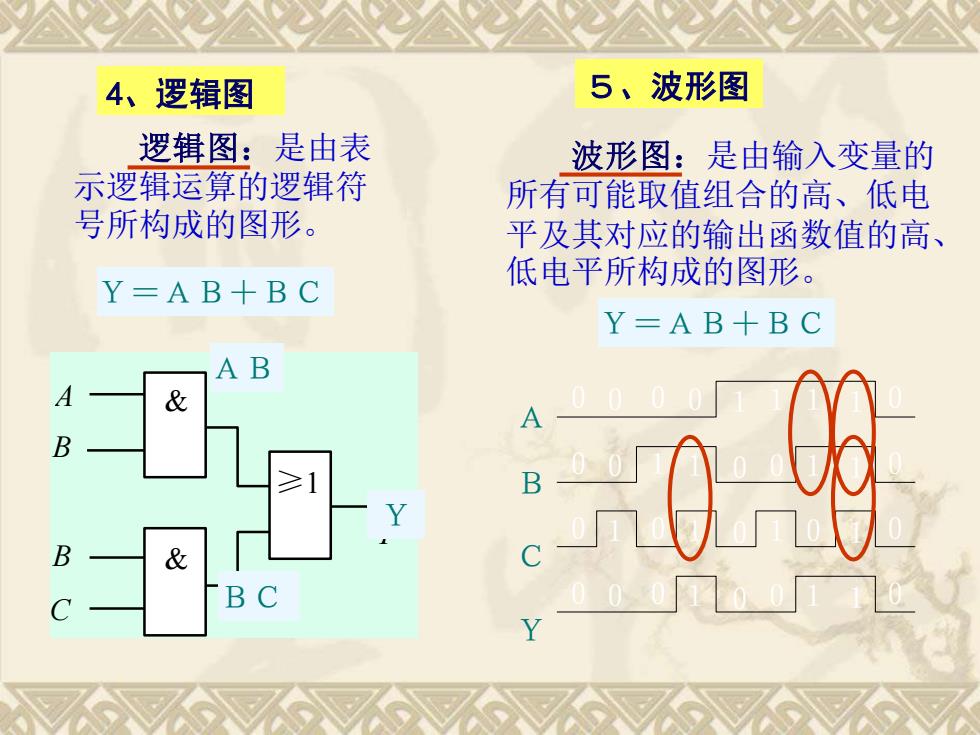
4、逻辑图 5、波形图 逻辑图:是由表 波形图:是由输入变量的 示逻辑运算的逻辑符 所有可能取值组合的高、低电 号所构成的图形。 平及其对应的输出函数值的高、 低电平所构成的图形。 Y=AB+BC Y=AB+BC & B 0的
4、逻辑图 逻辑图:是由表 示逻辑运算的逻辑符 号所构成的图形。 Y=AB+BC Y & ≥1 & A B B C AB BC 5、波形图 波形图:是由输入变量的 所有可能取值组合的高、低电 平及其对应的输出函数值的高、 低电平所构成的图形。 Y=AB+BC A B C Y 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 0 1 1 0 1 1 1 1 1 0 0 0 0 Y
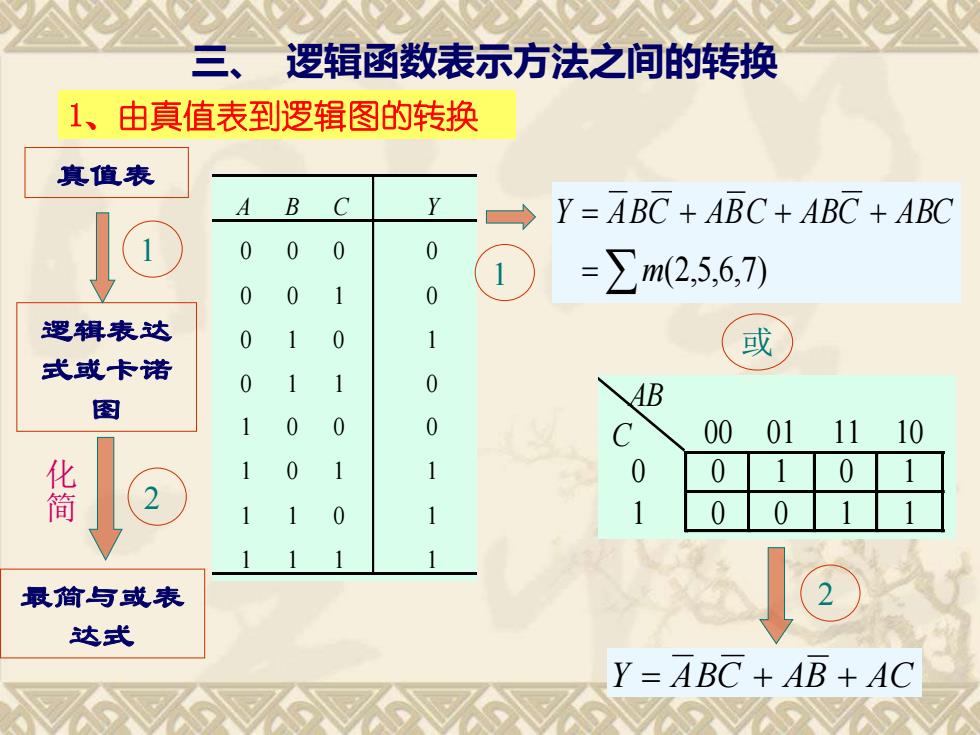
逻辑函数表示方法之间的转换 1、由真值表到逻辑图的转换 真值表 B C Y=ABCABC+ABC ABC 0 0 0 0 0 0 =∑m256,7) 1 0 逻辑表达 0 1 0 1 或 式或卡诺 0 1 1 0 图 AB 1 0 0 0 C 00 01 1110 告 1 0 1 1 0 0 1 0 2 1 1 0 1 0 0 1 1 最简与或表 达式 Y=ABC+AB+AC
三、 逻辑函数表示方法之间的转换 1、由真值表到逻辑图的转换 真值表 逻辑表达 式或卡诺 图 A B C Y 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 0 1 0 0 1 1 1 = = + + + m(2,5,6,7) Y ABC ABC ABC ABC 1 1 AB C 00 01 11 10 0 0 1 0 1 1 0 0 1 1 最简与或表 达式 化 简 2 或 Y = ABC + AB + AC 2