
第8章数字通信中的信道编码 第8章数字通信中的信道编码 可数字通信信号在传输过程中因信道失真、噪声和干扰的影响,导致接收端解调检测后 的误码率达不到实用要求,例如话音通信的误码率高于102,数据通信的误码率高于 10;一般都需要进行纠错编码,使之降低到希望达到的误码率。 。依据有噪声信道编码定理(又称香农第二定理),只要通信速率小于信道容量,则存在 一种编码,使得误码率任意小,这为采用信道编码提供了理论依据: ◆信道编码大致可分为两大类,一类是随机码编码,利用概率方法分析编码信号的性能, 对特定信道通信:这种方法可给出错误概率限,但在实际中难于实现,香农在推导信道 容量公式时,就是利用了随机编码,假定所采用的信道编码完全随机而且无限长。 ◆另一类是基于代数理论的代数编码和基于概率论的概率编码,前者主要包含分组码,后 者主要包含卷积码、级联码、乘积码、格形编码调制以及Tubo码。 ◆代数编码理论主要是研究对于给定的码率(即编码前后数据率之比),寻找可以最大化最 小距离的码字;而概率编码理论则偏重于寻找在考虑编、译码复杂度基础上优化平均性 能的码字。 ◆基于代数理论和基于概率理论的编码易于实现,是本章的主要内容。 8.1编码器设计中多种因素的权衡 8.1.1编码增益及其极限 香农推导出的有限带宽AWGN波形信道的容量公式为: C=w1oe,+N)(bps (8-1-1) 其中W2)为信道带宽,P为信号功率,N为噪声功率谱密度,P/(N,W)为信噪比 设一个信息速率为R,(bs)数据流,以码率为r=k1n进行信道编码后其速率变为R,/r: 如果使它通过一条基于BPSK调制、带宽为W的波形信道以最高速率-W(bs)传输,则要 实现几乎无误码传输必须满足下式: (8-1-2) 西安电子科技大学 1
第 8 章 数字通信中的信道编码 西安电子科技大学 1 第 8 章 数字通信中的信道编码 ) 数字通信信号在传输过程中因信道失真、噪声和干扰的影响,导致接收端解调检测后 的误码率达不到实用要求,例如话音通信的误码率高于 10-2,数据通信的误码率高于 10-6;一般都需要进行纠错编码,使之降低到希望达到的误码率。 ) 依据有噪声信道编码定理(又称香农第二定理),只要通信速率小于信道容量,则存在 一种编码,使得误码率任意小,这为采用信道编码提供了理论依据; 信道编码大致可分为两大类,一类是随机码编码,利用概率方法分析编码信号的性能, 对特定信道通信;这种方法可给出错误概率限,但在实际中难于实现,香农在推导信道 容量公式时,就是利用了随机编码,假定所采用的信道编码完全随机而且无限长。 另一类是基于代数理论的代数编码和基于概率论的概率编码,前者主要包含分组码,后 者主要包含卷积码、级联码、乘积码、格形编码调制以及 Turbo 码。 代数编码理论主要是研究对于给定的码率(即编码前后数据率之比),寻找可以最大化最 小距离的码字;而概率编码理论则偏重于寻找在考虑编、译码复杂度基础上优化平均性 能的码字。 基于代数理论和基于概率理论的编码易于实现,是本章的主要内容。 8.1 编码器设计中多种因素的权衡 8.1.1 编码增益及其极限 香农推导出的有限带宽 AWGN 波形信道的容量公式为: 2 0 log (1 ) P C W N W = + (bps) (8-1-1) 其中 W(Hz)为信道带宽, P 为信号功率,N0为噪声功率谱密度, 0 P /( ) N W 为信噪比。 设一个信息速率为 Rb (bps)数据流,以码率为 r kn = / 进行信道编码后其速率变为 Rb /r ; 如果使它通过一条基于 BPSK 调制、带宽为W 的波形信道以最高速率-W (bps)传输,则要 实现几乎无误码传输必须满足下式: Rb = r W < 2 0 log (1 ) P W WN + (bps) (8-1-2)

第8章数字通信中的信道编码 <1og1+ N。 (8-1-3) 或 5,- N。r (8-1-4a) 如果调制方式是2PAM数字调制,并以基带信号方式传输,则其最大传输速率为 2W(bps),因而上式应改为 (8-1-4b) 105 BSPK 10 8.87dB 10.3dB 12.1d 10 =12 o10 2160181622 4 6 810 88 /%a) 图8.I-】BPSK调制带通传输有无编码的误码特性比较 8.12不同误码率下码率与信噪比的关系 ■上面给出的码率与信噪比的关系是在几乎无误码的可靠通信前提下推出的,而在实际 应用中常常容许误码率就可进行正常通信: ■对于任意一种误码率要求,波形信道结合误编码进行传输时所对应的最低E,/N,值, 都是可以用香农公式计算的:这种对应关系本质上就是香农限失真编码定理的内含。 ■如果对于k信息比特可以容忍P。的平均误比特率,则可以将R信息表示为 R1-MP)》,其中Mx)为二进制嫡函数-Mx)=-xog2x-1-x)log,-x)。这样,实 现正常通信应该满足的条件为 西安电子科技大学
第 8 章 数字通信中的信道编码 西安电子科技大学 2 设每比特的信号能量为 Eb ,则信噪比可表示为: 0 00 0 P ER E R E bb b b b r WN WN N W N == = ,代入上式得 2 0 log 1 b rE Wr W N ⎛ ⎞ (8-1-4a) 如果调制方式是 2PAM 数字调制,并以基带信号方式传输,则其最大传输速率为 2W (bps),因而上式应改为 2 0 2 1 2 r Eb N r − > (8-1-4b) 图 8.1-1 BPSK 调制带通传输有无编码的误码特性比较 8.1.2 不同误码率下码率与信噪比的关系 上面给出的码率与信噪比的关系是在几乎无误码的可靠通信前提下推出的,而在实际 应用中常常容许误码率就可进行正常通信; 对于任意一种误码率要求,波形信道结合误编码进行传输时所对应的最低 0 / E N b 值, 都是可以用香农公式计算的;这种对应关系本质上就是香农限失真编码定理的内含。 如果对于 k 信息比特可以容忍 kPb 的平均误比特率,则可以将 Rb 信息表示为 (1 ( )) R hP b b − ,其中 h x( ) 为二进制熵函数- 2 2 hx x x x x ( ) log (1 )log (1 ) = − −− − 。这样,实 现正常通信应该满足的条件为
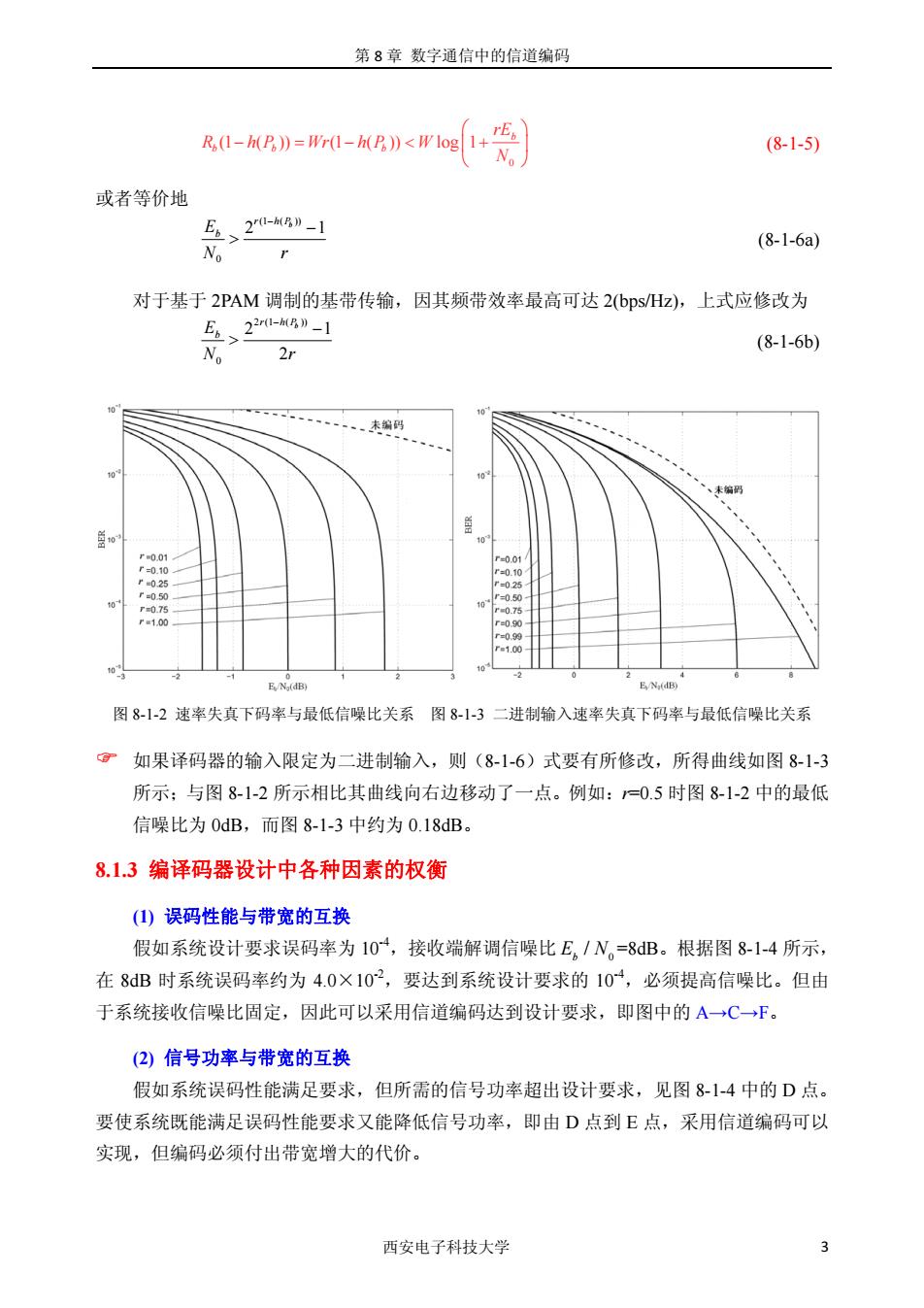
第8章数字通信中的信道编码 -》=- (8-1-5) 或者等价地 (8-1-6a) 对于基于2PAM调制的基带传输,因其频带效率最高可达2bps/Hz),上式应修改为 、2-》-1 No 2r (8-1-6b) F./N(dB 图81-2速率失真下码率与最低信噪比关系图8-3二进制输入速率失真下码率与最低信噪比关系 g如果译码器的输入限定为二进制输入,则(81-6)式要有所修改,所得曲线如图8-13 所示:与图8-1-2所示相比其曲线向右边移动了一点。例如:=0.5时图81-2中的最低 信噪比为0dB,而图8-l-3中约为0.18dB。 8.1.3编译码器设计中各种因素的权衡 ()误码性能与带宽的互换 假如系统设计要求误码率为10,接收端解调信噪比E。/N。=8dB。根据图8-1-4所示, 在8B时系统误码率约为4.0×102,要达到系统设计要求的10,必须提高信噪比。但由 于系统接收信噪比固定,因此可以采用信道编码达到设计要求,即图中的A→C→F。 (2)信号功率与带宽的互换 假如系统误码性能满足要求,但所需的信号功率超出设计要求,见图814中的D点 要使系统既能满足误码性能要求又能降低信号功率,即由D点到E点,采用信道编码可以 实现,但编码必须付出带宽增大的代价。 西安电子科技大学
第 8 章 数字通信中的信道编码 西安电子科技大学 3 0 (1 ( )) (1 ( )) log 1 b bb b rE R h P Wr h P W N ⎛ ⎞ − =− (8-1-6a) 对于基于 2PAM 调制的基带传输,因其频带效率最高可达 2(bps/Hz),上式应修改为 2 (1 ( )) 0 2 1 2 b r hP Eb N r − − > (8-1-6b) 图 8-1-2 速率失真下码率与最低信噪比关系 图 8-1-3 二进制输入速率失真下码率与最低信噪比关系 ) 如果译码器的输入限定为二进制输入,则(8-1-6)式要有所修改,所得曲线如图 8-1-3 所示;与图 8-1-2 所示相比其曲线向右边移动了一点。例如:r=0.5 时图 8-1-2 中的最低 信噪比为 0dB,而图 8-1-3 中约为 0.18dB。 8.1.3 编译码器设计中各种因素的权衡 (1) 误码性能与带宽的互换 假如系统设计要求误码率为 10-4,接收端解调信噪比 0 / E N b =8dB。根据图 8-1-4 所示, 在 8dB 时系统误码率约为 4.0×10-2,要达到系统设计要求的 10-4,必须提高信噪比。但由 于系统接收信噪比固定,因此可以采用信道编码达到设计要求,即图中的 A→C→F。 (2) 信号功率与带宽的互换 假如系统误码性能满足要求,但所需的信号功率超出设计要求,见图 8-1-4 中的 D 点。 要使系统既能满足误码性能要求又能降低信号功率,即由 D 点到 E 点,采用信道编码可以 实现,但编码必须付出带宽增大的代价

第8章数字通信中的信道编码 已编码 10 2 6 12 16 图8-】4有无纠错编码的数字调制传输系统的误码特性比较 (③)以较低带宽代价提高信息速率 假如系统要求误码率为10,如图中的D点。如果希望系统传输更高的信息速率,与 原先的速率相比,这样将导致每比特的能量降低,可能使得图中的D点移到B点,此时虽 然满足了速率要求,但误码率升高而不能满足要求;而利用编码可使B点移到E点,使误 码率也满足要求,其代价是由于编码而需要更宽的带宽:但采用好的编码方法只需付出较 小的带宽代价。 (4编译码复杂度与性能的权衡 在系统功率及带宽都受限的情况下,可以通过编译码算法的复杂度来换取系统误码性 能的改善。 ①分组码可以通过增加编码的分组长度,译码采用最大似然译码来改善性能: ②卷积码可以通过增加约束长度,译码采用最大似然序列译码来改善性能:采用软判 决译码一般比硬判决译码有2dB左右的增益: ③采用级联码性能一般要比单码性能有改善: ④对于逼近香农限的Tubo及LDPC码,通过译码迭代次数可以明显改善误码性能: 采用较好的编译码算法也可以导致误码性能的改善。 (⑤编码增益零点 ■交叉点是由于两种相反因素平衡的结果: ◆ 一个是编码时相对于未编码系统加入了冗余,降低了每比特的能量而使误码率增大: 另一方面,这些冗余在接收端可以纠正传输中引入的错误,而使误码率降低: 二者在交叉点处达到平衡。在交叉点以下,冗余带来误码率降低的收益,大于因能量 西安电子科技大学
第 8 章 数字通信中的信道编码 西安电子科技大学 4 图 8-1-4 有无纠错编码的数字调制传输系统的误码特性比较 (3) 以较低带宽代价提高信息速率 假如系统要求误码率为 10-6,如图中的 D 点。如果希望系统传输更高的信息速率,与 原先的速率相比,这样将导致每比特的能量降低,可能使得图中的 D 点移到 B 点,此时虽 然满足了速率要求,但误码率升高而不能满足要求;而利用编码可使 B 点移到 E 点,使误 码率也满足要求,其代价是由于编码而需要更宽的带宽;但采用好的编码方法只需付出较 小的带宽代价。 (4) 编译码复杂度与性能的权衡 在系统功率及带宽都受限的情况下,可以通过编译码算法的复杂度来换取系统误码性 能的改善。 ①分组码可以通过增加编码的分组长度,译码采用最大似然译码来改善性能; ②卷积码可以通过增加约束长度,译码采用最大似然序列译码来改善性能;采用软判 决译码一般比硬判决译码有 2dB 左右的增益; ③采用级联码性能一般要比单码性能有改善; ④对于逼近香农限的 Turbo 及 LDPC 码,通过译码迭代次数可以明显改善误码性能; 采用较好的编译码算法也可以导致误码性能的改善。 (5) 编码增益零点 交叉点是由于两种相反因素平衡的结果; 一个是编码时相对于未编码系统加入了冗余,降低了每比特的能量而使误码率增大; 另一方面,这些冗余在接收端可以纠正传输中引入的错误,而使误码率降低; ¾ 二者在交叉点处达到平衡。在交叉点以下,冗余带来误码率降低的收益,大于因能量

第8章数字通信中的信道编码 消耗带来误码率升高的损失,因而能获得编码增益:这就是在同一信噪比下误码率得 到改善,或在达到相同误码率时所需信噪比可降低,降低的倍数就是编码增益:当然 在不同误码率级别上能获得的编码增益是不同的。 >在交叉点以上,冗余所引起能量损失的负面影响超过了纠错码纠错带来的好处,因此 纠错编码反而使误码特性变差:这是因为信噪太低,所产生的误码率超出了纠错码的 纠错能力,以至于越纠越错,误码率反而增大。 8.2差错类型及差错控制方式 ◆对于差错的控制方式,分为自动检错重发方式(ARQ)和前向纠错方式(FEC)。 ◆ARQ是一类实现高可靠性传输的检错重传技术,它无需复杂的纠错设备,实现相对 简单。ARQ方式的编码只需要有检错能力,如奇偶校验码、循环冗余检验CRC码 在接收端通过检错来决定是否需要重传。 ◆下EC方式是单向的,在接收端通过纠错来降低误码率,因此所用编码要有纠错功能 如分组码、卷积码等。与ARQ方式相比,FEC方式的码编码与译码实现方法都要 复杂得多。 ()检错重发方式 使够发现错误的码 发送端 接收端 应答信号 图8-2-1ARQ原理框图 ARQ的主要优点: ①只需要少量的多余码元(如5%-20%)就能获得极低的输出误码率。 ②要求使用的检错码基本上与信道编码的差错统计特性无关,能适用于各种类型信道。 ③实现成本和复杂性很低, ARQ的主要缺点: ①由于需要反向信道,故不能用于单向传输系统,也难以用于广播系统的重发控制。 ②当信道传输性能很差时,系统可能处于重发循环中而使通信效率低甚至不能通信。 ③不适于实时性、连续性要求较高的通信业务。 (2)前向纠错方式(FEC) 发送端发送能够纠正错误的码,接收端收到后通过纠错码自动纠正传输中的错误,特 点是单向传输。与ARQ方式相比,FEC方式的优点是不需要重传,无需反向信道,延时小, 实时性好:其缺点是编码与译码方法都要复杂,编码效率较低,所选用的纠错码须与信道 特性相匹配。同时每种编码都有一定的纠错能力,误码超出纠错范围将导致误码更加恶化。 西安电子科技大学
第 8 章 数字通信中的信道编码 西安电子科技大学 5 消耗带来误码率升高的损失,因而能获得编码增益;这就是在同一信噪比下误码率得 到改善,或在达到相同误码率时所需信噪比可降低,降低的倍数就是编码增益;当然 在不同误码率级别上能获得的编码增益是不同的。 ¾ 在交叉点以上,冗余所引起能量损失的负面影响超过了纠错码纠错带来的好处,因此 纠错编码反而使误码特性变差;这是因为信噪太低,所产生的误码率超出了纠错码的 纠错能力,以至于越纠越错,误码率反而增大。 8.2 差错类型及差错控制方式 对于差错的控制方式,分为自动检错重发方式(ARQ)和前向纠错方式(FEC)。 ARQ 是一类实现高可靠性传输的检错重传技术,它无需复杂的纠错设备,实现相对 简单。ARQ 方式的编码只需要有检错能力,如奇偶校验码、循环冗余检验 CRC 码, 在接收端通过检错来决定是否需要重传。 FEC 方式是单向的,在接收端通过纠错来降低误码率,因此所用编码要有纠错功能, 如分组码、卷积码等。与 ARQ 方式相比,FEC 方式的码编码与译码实现方法都要 复杂得多。 (1) 检错重发方式 图 8-2-1 ARQ 原理框图 ARQ 的主要优点: ① 只需要少量的多余码元(如 5%-20%)就能获得极低的输出误码率。 ② 要求使用的检错码基本上与信道编码的差错统计特性无关,能适用于各种类型信道。 ③ 实现成本和复杂性很低。 ARQ 的主要缺点: ① 由于需要反向信道,故不能用于单向传输系统,也难以用于广播系统的重发控制。 ② 当信道传输性能很差时,系统可能处于重发循环中而使通信效率低甚至不能通信。 ③ 不适于实时性、连续性要求较高的通信业务。 (2) 前向纠错方式(FEC) 发送端发送能够纠正错误的码,接收端收到后通过纠错码自动纠正传输中的错误,特 点是单向传输。与 ARQ 方式相比,FEC 方式的优点是不需要重传,无需反向信道,延时小, 实时性好;其缺点是编码与译码方法都要复杂,编码效率较低,所选用的纠错码须与信道 特性相匹配。同时每种编码都有一定的纠错能力,误码超出纠错范围将导致误码更加恶化

第8章数字通信中的信道编码 发送滑可以斜正错误的仍技收璃 图8-2-2FEC原理框图 (3)混合纠错方式(HEC) 发送端发送既能自动纠错又能检测的码。接收端收到码流后,检查差错情况,如果错 误在纠错能力范围以内,则自动纠错:如果超过了纠错能力,但能检测出来,则经过反馈 信道请求发送端重发。HEC的性能及优缺点介于ARQ与FEC之间。 能够发现和纠正误的码 发送端 接收端 应答信号 图8-2-3HEC原理框图 8.3分组码 意分组码是将长度为k的数字向量映射为长度为n的数字向量(>k),从而引入元余的 一种编码方法。 。如果映射是线性的,则所产生的码就是线性码,否则为非线性码。通常数字信号处理 的信息是二进制的,因此这种映射一般是针对二进制信号的。 8.3.1有限域FG(q) 编译码的功能体现为对码字进行乘、加算术运算。在有限(q)个元素的集合构成的域中, 进行乘加算术运算服从代数运算的惯例,如:封闭性、结合率、交换率、分配率都成立: 域中存在零元素、每个非零元素都存在对应的逆元素、存在一个单位元素。有限域只有当9 为质数或质数的m次方(q)时才能构成,它们都是基于模运算。 与实数域、复数域和整数域的算术运算相比,FG(q)主要有以下几个不同点: 1)FG(q)是采用模q运算来保证其封闭性:例如:a,b∈FG(q),则c=a+b∈FG(q) 相当于整数域中c=(a+b)modg 2)乘法的逆元素与加法的逆元素相同,b=-b,因此a/b定义为ab=a(-b): 3)多维有限域空间中两个矢量的之间的距离定义为汉明距离,但内积、正交的概念与 多维欧几里德空间的相似。 8.3.2分组码的基本概念 定义:(m,)的分组码是由2个长度都为n的码字构成的集合,用来对k比特信息进行 西安电子科技大学
第 8 章 数字通信中的信道编码 西安电子科技大学 6 图 8-2-2 FEC 原理框图 (3) 混合纠错方式(HEC) 发送端发送既能自动纠错又能检测的码。接收端收到码流后,检查差错情况,如果错 误在纠错能力范围以内,则自动纠错;如果超过了纠错能力,但能检测出来,则经过反馈 信道请求发送端重发。HEC 的性能及优缺点介于 ARQ 与 FEC 之间。 图 8-2-3 HEC 原理框图 8.3 分组码 ) 分组码是将长度为 k 的数字向量映射为长度为 n 的数字向量(n>k),从而引入冗余的 一种编码方法。 ) 如果映射是线性的,则所产生的码就是线性码,否则为非线性码。通常数字信号处理 的信息是二进制的,因此这种映射一般是针对二进制信号的。 8.3.1 有限域 FG( q ) 编译码的功能体现为对码字进行乘、加算术运算。在有限( q )个元素的集合构成的域中, 进行乘加算术运算服从代数运算的惯例,如:封闭性、结合率、交换率、分配率都成立; 域中存在零元素、每个非零元素都存在对应的逆元素、存在一个单位元素。有限域只有当 q 为质数或质数的 m 次方( q m)时才能构成,它们都是基于模运算。 与实数域、复数域和整数域的算术运算相比,FG( q )主要有以下几个不同点: 1)FG( q )是采用模 q运算来保证其封闭性;例如:a b, ∈FG( q ),则c = a b + ∈FG( q), 相当于整数域中c = mod ( ) q a b + 。 2)乘法的逆元素与加法的逆元素相同,b-1=-b,因此 ( ) 1 a b ab a b / − 定义为 = − ; 3)多维有限域空间中两个矢量的之间的距离定义为汉明距离,但内积、正交的概念与 多维欧几里德空间的相似。 8.3.2 分组码的基本概念 定义:(, ) n k 的分组码是由 2k 个长度都为 n 的码字构成的集合,用来对 k 比特信息进行

第8章数字通信中的信道编码 编码,每个码字都是一个n维矢量:q进制分组码其码字矢量的元素取值于有限域FG(q): {0,1,q-},即每个码字中的元素都是从{0,1,q-中选取的。 码率:长度n的二进制分组码有2种可能的码字,从中选择M个码字作为可用码, M=2(k<),而其余2”-2*个码为禁用码。这样k比特的一块数据经编码后映射为一个n 比特的数据块,这就是(m,k)的分组码。其码率定义为R=k/n。 码字重量:码字包含的非零元素的个数。如果全部M个码字具有相同的重量,这种码 称为恒重码。 汉明距离:任意两个码字C,和C,对应位置上元素不同的总个数,记为d。如(7,3)分 组码中的两个码字(0111010)与(0011101)的汉明距离为4。汉明距离满足三角不等式, 即若CCCk为同一码组中的不同码字,则d+d2d 线性码:设C,和C,为某(m,k)分组码的两个码字,a和a是码元字符集里任意两个元 素,若α,C+a,C,也是该码的一个码字,则这种分组码称为线性码。线性码必包含全零码: 恒重码是非线性码。 最小码距d:M个码字集合中汉明距离{d,}的最小值称为最小码距,最小码距关系 者该码字的检错与纠错能力。(n,)饯性分组码最小距离等于dm的充要条件是校验矩阵H 中任何dmml列线性无关。 零空间:(m,k)分组码构成k维空间是n维矢量空间的子空间,记为S。,其中任意k个 线性无关的矢量可构成“基底”。如果n维矢量空间S中存在另一组矢量,它们与S的基底” 都正交,则这组矢量构成的子空间称为S的零空间,其维数必定等于(-k)。零空间与(m,k) 分组码的生成矩阵G和监督矩阵H之间存在紧密联系。 检错能力:假如编码码元C通过噪声干扰信道传输,接收码元R在j个位置出现错误, 则dC,Rj。若该分组码的最小汉明距为dmm,这意味着该码组中任意两个码字至少在dmm 个位置上不同,因此dmm1或更少的错误将使R不是该码组中的码字。当接收端发现接收 码字是非法码字(非码组中的码)时,就认为检测到了错误。当错误位置大于等于dm时, 由于至少存在一对合法码字的汉明距满足dmm,因此该分组码不可能检测到所有dmm个错误, 这使得分组码的检错能力为dmml。 纠错能力:令1为满足2+1sdm≥2什2的正整数。其纠错能力为=(dmm1)2。 系统码:系统码是指其编码输出信息块中完全保留输入信息块的编码方法。编码输出 的原始信息位也叫系统位。(,k)分组码中,系统码通常指前k位为原始信息位。 根据信息码元与监督码元的函数关系,分为线性码和非线性码。 根据信息码元和监督码元之间的约束方式,分为分组码和卷积码。在分组码中,监督 西安电子科技大学 7
第 8 章 数字通信中的信道编码 西安电子科技大学 7 编码,每个码字都是一个 n 维矢量;q 进制分组码其码字矢量的元素取值于有限域 FG( q ): {0, 1, ., 1} q − ,即每个码字中的元素都是从{0, 1, ., 1} q − 中选取的。 码率:长度 n 的二进制分组码有 2n 种可能的码字,从中选择 M 个码字作为可用码, M = 2k ( ) k n < ,而其余 2 2 n k − 个码为禁用码。这样 k 比特的一块数据经编码后映射为一个 n 比特的数据块,这就是(, ) n k 的分组码。其码率定义为 / R kn c = 。 码字重量:码字包含的非零元素的个数。如果全部 M 个码字具有相同的重量,这种码 称为恒重码。 汉明距离:任意两个码字Ci 和Cj 对应位置上元素不同的总个数,记为 ij d 。如(7,3)分 组码中的两个码字(0111010)与(0011101)的汉明距离为 4。汉明距离满足三角不等式, 即若 Ci、Cj、Ck 为同一码组中的不同码字,则 dik+djk≥dij。 线性码:设Ci 和Cj 为某 (, ) n k 分组码的两个码字,α1和α 2 是码元字符集里任意两个元 素,若α1 2 C C +α j 也是该码的一个码字,则这种分组码称为线性码。线性码必包含全零码; 恒重码是非线性码。 最小码距 min d : M 个码字集合中汉明距离{ }ij d 的最小值称为最小码距,最小码距关系 着该码字的检错与纠错能力。(n,k)线性分组码最小距离等于 dmin 的充要条件是校验矩阵 H 中任何 dmin-1 列线性无关。 零空间:(,) n k 分组码构成 k 维空间是 n 维矢量空间 S 的子空间,记为 c S ,其中任意 k 个 线性无关的矢量可构成“基底”。如果 n 维矢量空间 S 中存在另一组矢量,它们与 c S 的“基底” 都正交,则这组矢量构成的子空间称为 c S 的零空间,其维数必定等于( ) n k − 。零空间与 (, ) n k 分组码的生成矩阵 G 和监督矩阵 H 之间存在紧密联系。 检错能力:假如编码码元 C 通过噪声干扰信道传输,接收码元 R 在 j 个位置出现错误, 则 d(C,R)=j。若该分组码的最小汉明距为 dmin,这意味着该码组中任意两个码字至少在 dmin 个位置上不同,因此 dmin-1 或更少的错误将使 R 不是该码组中的码字。当接收端发现接收 码字是非法码字(非码组中的码)时,就认为检测到了错误。当错误位置大于等于 dmin时, 由于至少存在一对合法码字的汉明距满足dmin,因此该分组码不可能检测到所有dmin个错误, 这使得分组码的检错能力为 dmin-1。 纠错能力:令 t 为满足 2t+1≤dmin≥2t+2 的正整数。其纠错能力为 t=(dmin -1)/2。 系统码: 系统码是指其编码输出信息块中完全保留输入信息块的编码方法。编码输出 的原始信息位也叫系统位。(n,k)分组码中,系统码通常指前 k 位为原始信息位。 根据信息码元与监督码元的函数关系,分为线性码和非线性码。 根据信息码元和监督码元之间的约束方式,分为分组码和卷积码。在分组码中,监督

第8章数字通信中的信道编码 码元仅与本码组的信息码元有关,而在卷积码中,监督码元不仅与本组的信息码元有关, 还与前面若干组的信息码元有关。 8.3.3生成矩阵与校验矩阵 设编码器输入为Xn=x1,x,xt小,输出矢量为Cn=c,cn2,C】,对于二进制线 性分组码,编码运算可用n个方程表示: Cw =xmi8+x+j=1.2.n (8-3-8) 改写成矩阵形式:Cn=XG,其中 「81「81812.gm G=8 88.8 (8-3-9) 称为生成矩阵,{g}是(m,k)分组码的基底。 >如:n=8,k=6,即每输入6比特,编码成一个8比特的码字。可以看出,线性分组 码的编码码元为生成矩阵各列向量的线性组合,线性组合的系数为输入的信息序列。 (m,k)分组码的生成矩阵G都可通过初等变换简化成如下的系统码形式: [100.0A1Pa.PA-t ::::ξ: (8-3-10) 000 1 PuPia.p-4J 其中I4是k×k的单位矩阵,P是(n-k)×(n-k)的矩阵,P决定(n-k)个冗余比特。 任何一个(m,k)分组码都存在一个n-k维对偶码,对偶码是由零空间中n-k个线性无关 的码矢量组成,其生成矩阵表示为H。由于(m,k)码中任意一个码字C均与其对偶码的各 码字正交,因此(m,)码的任意码字必正交于矩阵H的每一行,可得 m,CHT=0或GHT=0 (8-3-11) 可见矩阵H可以用来检错,因而称为(m,)码的校验矩阵。 ■线性分组码可以由一个校验矩阵H等效描述,所有码字C=(1,02,c)均满足 HC0。校验矩阵的每一行表示一个校验约束关系,行中不为零的码元变量参与了 该行的校验方程。 若G是系统生成矩阵,则对偶码的生成矩阵: 西安电子科技大学
第 8 章 数字通信中的信道编码 西安电子科技大学 8 码元仅与本码组的信息码元有关,而在卷积码中,监督码元不仅与本组的信息码元有关, 还与前面若干组的信息码元有关。 8.3.3 生成矩阵与校验矩阵 设编码器输入为 1 2 [ , , ., ] X xx x m m m mk = ,输出矢量为 1 2 [ , , ., ] C cc c m m m mn = ,对于二进制线 性分组码,编码运算可用 n 个方程表示: 11 2 2 . 1,2,., mj m j m j mk kj c xg xg xg j n = + ++ = (8-3-8) 改写成矩阵形式:C XG m m = ,其中 1 11 12 1 2 21 22 2 1 2 n n k k k kn g gg g g gg g G g gg g ⎡ ⎤ ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ = = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦ " " # ## # " (8-3-9) 称为生成矩阵,{gi} 是(, ) n k 分组码的基底。 ¾ 如: n k = = 8, 6 ,即每输入 6 比特,编码成一个 8 比特的码字。可以看出,线性分组 码的编码码元为生成矩阵各列向量的线性组合,线性组合的系数为输入的信息序列。 (, ) n k 分组码的生成矩阵G 都可通过初等变换简化成如下的系统码形式: 11 12 1 21 22 2 1 2 100 0 010 0 [ ] 000 1 n k n k k k k kn k pp p pp p G IP pp p − − − ⎡ ⎤ ⎢ ⎥ = = ⎣ ⎦ " " " " ## # ## # " " (8-3-10) 其中 Ik 是 k k × 的单位矩阵,P 是( )( ) nk nk −×− 的矩阵,P 决定( ) n k − 个冗余比特。 任何一个(, ) n k 分组码都存在一个 n k − 维对偶码,对偶码是由零空间中 n k − 个线性无关 的码矢量组成,其生成矩阵表示为 H 。由于 (, ) n k 码中任意一个码字Cm 均与其对偶码的各 码字正交,因此(, ) n k 码的任意码字必正交于矩阵 H 的每一行,可得 , T ∀ = mCHm 0或 T GH = 0 (8-3-11) 可见矩阵 H 可以用来检错,因而称为(, ) n k 码的校验矩阵。 线性分组码可以由一个校验矩阵 H 等效描述,所有码字 C=(c1,c2,.,cn)均满足 HCT =0T 。校验矩阵的每一行表示一个校验约束关系,行中不为零的码元变量参与了 该行的校验方程。 若G 是系统生成矩阵,则对偶码的生成矩阵:

第8章数字通信中的信道编码 H=IPT L] (8-3-12) 设C,代表(n,k)码中重量最小的码字,则其重量就是该码的最小距离d。由C,=0, 可知H的秩≤d-1。由零空间的性质可知H的秩为n-k,则得 d≤n-k+l (8-3-13) 【定理】(n,k)线性分组码最小距离等于d的充要条件是H矩阵中任何d-1列线性无关。 【例】(7,4)汉明码编码 (7,4)分组码的形式为Aa6a5a4aa2a1a,其中aa5aa为信息码元,aaa为监 督码元,监督码元与信息码元的关系为: a,+a+a+a=0 a=a。+a+a或者a。+a+a+a-0 (8-3-14) ao as +as +as a+a+a+a。=0 写成矩阵形式: HA=0 (8-3-15) 「1110100 其中矩阵1101010就是校验矩阵,0=0:H=P,P为r×K的矩阵 1011001 0 I为r阶单位阵。如将方程补充完整,则有 a6=a6 [a1f1000] as=ds 0100 a =a, 0010a a3=d3 人 或a 0001 (8-3-16) a. a=a6+a5+a 1110 a=as +as+a /9 1101La do asas ay a 1011 「1000111门 其中矩阵 0100110 就是为生成矩阵G,可表示为GIP]:利用信息序列与生 0010101 0001011 成矩阵就可以产生编码码元。此码共有8个码字,如表8-3-1所示。 西安电子科技大学
第 8 章 数字通信中的信道编码 西安电子科技大学 9 [ ] T H PI = n k − (8-3-12) 设Cj 代表(, ) n k 码中重量最小的码字,则其重量就是该码的最小距离 min d 。由 T C Hj = 0 , 可知 H 的秩 min ≤ − d 1。由零空间的性质可知 H 的秩为 n k − ,则得 min d nk ≤ − +1 (8-3-13) 【定理】(n,k)线性分组码最小距离等于 min d 的充要条件是 H 矩阵中任何 min d −1列线性无关。 【例】(7,4)汉明码编码 (7,4)分组码的形式为 A=[a6 a5 a4 a3 a2 a1 a0],其中 a6a5a4a3为信息码元,a2a1a0为监 督码元,监督码元与信息码元的关系为: 2 654 1 653 0 643 a aaa aaaa a aaa ⎧ =++ ⎪ ⎨ =++ ⎪ ⎩ =++ 或者 6542 6531 6430 0 0 0 aaaa aaaa aaaa ⎧ + ++= ⎪ ⎨ + ++= ⎪ ⎩ + ++= (8-3-14) 写成矩阵形式: HA= 0 (8-3-15) 其中矩阵 H= 1110100 1101010 1011001 ⎡ ⎤ ⎢ ⎥ ⎣ ⎦ 就是校验矩阵,0 = 0 0 0 ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ;H =[P I],P 为 r×K 的矩阵, I 为 r 阶单位阵。如将方程补充完整,则有 6 6 5 5 4 4 3 3 2 654 1 653 0 643 a a a a a a a a a aaa aaaa a aaa ⎧ = ⎪ = ⎪ ⎪ = ⎪ ⎨ = ⎪ =++ ⎪ ⎪ =++ ⎪ ⎩ =++ 或 6 5 6 4 5 3 4 2 3 1 0 1000 0100 0010 0001 1110 1101 1011 a a a a a a a a a a a ⎡ ⎤ ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥⎡ ⎤ ⎢ ⎥ ⎢ ⎥⎢ ⎥ ⎢ ⎥ ⎢ ⎥ = ⎢ ⎥ ⎢ ⎥ ⎢ ⎥⎢ ⎥ ⎢ ⎥ ⎢ ⎥⎢ ⎥ ⎢ ⎥ ⎢ ⎥⎣ ⎦ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦ (8-3-16) 其中矩阵 1000111 0100110 0010101 0001011 ⎡ ⎤ ⎢ ⎥ ⎣ ⎦ 就是为生成矩阵 G,可表示为 G=[ I PT ];利用信息序列与生 成矩阵就可以产生编码码元。此码共有 8 个码字,如表 8-3-1 所示

第8章数字通信中的信道编码 表8-3-1(74)线性分组码 码字 码字 信息元信息元监督元信息元信息元监督元 00000000000 1000 1000111 00110011110 1011 1011001 01000100110 1100 1100001 010001001 0111011100011111111111 8.3.4伴随式译码 ■设发送的码字为C=(cm-1,cm-2.c1,co),信道产生的错误图样为E=(en-1,en-2.e 1,eo),则接收码字为R=C+E=(cn-+en-,cn-2+en-2.c+ebc0+eo),其中c 和e均为二进制数字,加法为模2加。 ■译码器的任务就是从R中恢复C,或者说是从R中估计E,如成功恢复,则译码 成功,否则译码错误。 伴随式定义为接收码字与校验矩阵之乘积,即 S=RHT=(C+E)HT=CHT+EHT (8-3-17) >由(8-1-3)式可知CH=0,因此S=RH=EH。 >如果没有错误传输,即E=0,则S=EH=0,若有错误传输,即E0,则S=EH0。 >对于确定的编码,H是已知的,因此仅S与信道错误图样E有关。如果能从S中得到 E,则可以从接收码字中正确恢复发送码字,即R+E=C+E+E=C。因此将S定义为接 收矢量R的伴随式或矫正子。线性分组码的一个重要性质是伴随式与错误图样是一 对应的。 如何从S中确定E,以便完成正确译码:为了能正确检错与纠错,校验矩阵H需满足: ①H中没有全0列,否则相应码字位置上的错误就无法影响伴随式,因而无法检测。 ②H中所有列都是惟一的;因为假如有两列相同的话,那么二者所对应的错误码发生 位置就无法识别。 我们以可纠正一位错误的线性分组码为例来说明伴随式与错误图样的关系。(,k)码共 有2个有效码字,由于错误图样不能为有效码字(否则无法检错与纠错),因此错误图样属 于2空间,错误图样有2个,这样可以构造出分组码的标准阵列,如表8-3-2所示。 表83-2分组码的标准阵列 西安电子科技大学 10
第 8 章 数字通信中的信道编码 西安电子科技大学 10 表 8-3-1 (7,4)线性分组码 码字 码字 信息元 信息元 监督元 信息元 信息元 监督元 0000 0000 000 1000 1000 111 0001 0001 011 1001 1001 100 0010 0010 101 1010 1010 010 0011 0011 110 1011 1011 001 0100 0100 110 1100 1100 001 0101 0101 101 1101 1101 010 0110 0110 011 1110 1110 100 0111 0111 000 1111 1111 111 8.3.4 伴随式译码 设发送的码字为 C=(cn – 1,cn – 2. c1,c0),信道产生的错误图样为 E=(en – 1,en – 2.e l ,e 0),则接收码字为 R=C+E=(cn – 1+ en – 1, cn – 2 + en – 2. c1+ e l, c0 + e 0),其中 ci 和 ei均为二进制数字,加法为模 2 加。 译码器的任务就是从 R 中恢复 C,或者说是从 R 中估计 E,如成功恢复,则译码 成功,否则译码错误。 伴随式定义为接收码字与校验矩阵之乘积,即 S=RHT =(C+E)HT =CHT +EHT (8-3-17) ¾ 由(8-1-3)式可知 CHT =0,因此 S=RHT =EHT 。 ¾ 如果没有错误传输,即 E=0,则 S = EHT =0,若有错误传输,即 E≠0,则 S =EHT ≠0。 ¾ 对于确定的编码,H 是已知的,因此仅 S 与信道错误图样 E 有关。如果能从 S 中得到 E,则可以从接收码字中正确恢复发送码字,即 R+E=C+E+E=C。因此将 S 定义为接 收矢量 R 的伴随式或矫正子。线性分组码的一个重要性质是伴随式与错误图样是一一 对应的。 如何从 S 中确定 E,以便完成正确译码;为了能正确检错与纠错,校验矩阵 H 需满足: ①H 中没有全 0 列,否则相应码字位置上的错误就无法影响伴随式,因而无法检测。 ② H 中所有列都是惟一的;因为假如有两列相同的话,那么二者所对应的错误码发生 位置就无法识别。 我们以可纠正一位错误的线性分组码为例来说明伴随式与错误图样的关系。(n,k)码共 有 2k 个有效码字,由于错误图样不能为有效码字(否则无法检错与纠错),因此错误图样属 于 2n-k 空间,错误图样有 2n-k个,这样可以构造出分组码的标准阵列,如表 8-3-2 所示。 表 8-3-2 分组码的标准阵列