
CHAPTER 8 Signal Modeling and Parametric Spectral Estimation 8.1 The Modeling Process:Theory and Practice 8.2 Estimation of All-Pole Models 8.3 Estimation Of Pole-Zero Models 8.4 Applications 8.5 Harmonic Models and Frequency Estimation Techniques 8.6 Summary
2 8.1 The Modeling Process: Theory and Practice 8.2 Estimation of All-Pole Models 8.3 Estimation Of Pole-Zero Models 8.4 Applications 8.5 Harmonic Models and Frequency Estimation Techniques 8.6 Summary CHAPTER 8 Signal Modeling and Parametric Spectral Estimation

8.1 The Modeling Process:Theory_and Practice Let's begin with what we've learnt before. 考虑输入为WGN信号,模型为PZP,Q)模型,描述其特征的差 分方程可表示为如下形式 x(n)-d:x(n-k)+o(n)d,o(n-k) (8.1.1) 对于该输出信号,其自功率谱密度可表示为 2 l+∑dea R(e)=o2|H(e0)P=o2 k=1 2D(e) A(e-jo)2 频率响应 ae-jok
8.1 The Modeling Process: Theory and Practice Let’s begin with what we’ve learnt before. 考虑输入为WGN信号,模型为PZ(P,Q)模型,描述其特征的差 分方程可表示为如下形式 对于该输出信号,其自功率谱密度可表示为 2 2 2 2 2 2 2 1 1 ( ) | ( ) | | ( ( )| 1 | | 1 ) Q j k k j P j j j k k j k k R H A e a d e e D e e e − − = − = − = = = + + 频率响应

8.1_The Modeling Process:Theory_and Practice +∑dea R(e)=H(ef)2 k= 2D(e-i) = A(e-)P 频率响应 1+∑aea k=1 What can we know from the above result? For a random signal,if we can estimate what model generates this signal and what the variance of excitation is,we can further estimate its autoPSD 0 l+∑de R(e)=6 k= =G2ID(e)p l+∑aem Ae)P k=
8.1 The Modeling Process: Theory and Practice 2 2 2 2 2 2 2 1 1 ( ) | ( ) | | ( ( )| 1 | | 1 ) Q j k k j P j j j k k j k k R H A e a d e e D e e e − − = − = − = = = + + 频率响应 • What can we know from the above result? • For a random signal, if we can estimate what model generates this signal and what the variance of excitation is, we can further estimate its autoPSD 2 2 2 1 1 2 2 | | ˆ 1 ˆ 1 ˆ ˆ ( ) ˆ ( ) | | ˆ ˆ ( ) Q j k k P k j k j j j k k d e D A e a e R e e − − = − − = = + = +

CHAPTER 8 Signal Modeling and Parametric Spectral Estimation What we gonna learn from this chapter? How to perform parametric spectral estimation in three stages: 1.Selection of an appropriate model for a given set of data 2.Estimation of the model parameters 3.Spectral estimation by using the obtained parametric model
5 How to perform parametric spectral estimation in three stages: 1. Selection of an appropriate model for a given set of data 2. Estimation of the model parameters 3. Spectral estimation by using the obtained parametric model CHAPTER 8 Signal Modeling and Parametric Spectral Estimation What we gonna learn from this chapter?
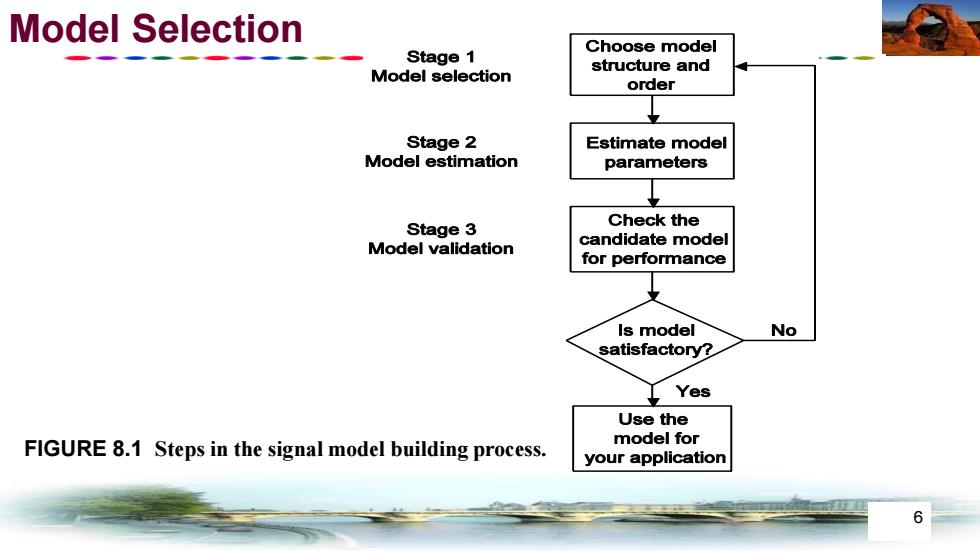
Model Selection Choose model Stage 1 structure and Model selection order Stage 2 Estimate model Model estimation parameters Stage 3 Check the Model validation candidate model for performance Is model No satisfactory? Use the FIGURE 8.1 Steps in the signal model building process. model for your application 6
6 Model Selection FIGURE 8.1 Steps in the signal model building process

Model Selection Now,we gonna briefly describe the three stages The model selection determines: 1 The complexity of the algorithm that estimates the model parameters. 2 The shape of the criterion function(quadratic or nonquadratic)
7 The model selection determines: ① The complexity of the algorithm that estimates the model parameters. ② The shape of the criterion function (quadratic or nonquadratic). Model Selection Now, we gonna briefly describe the three stages

Model Estimation Model estimation is also known as model fitting Particularly,we use the available data to estimate the parameters of the selected model,by using the optimization of some criteria(e.g.maximum likelihood,spectral matching)
• Model estimation is also known as model fitting • Particularly, we use the available data to estimate the parameters of the selected model, by using the optimization of some criteria (e.g. maximum likelihood, spectral matching). Model Estimation

Model Estimation In our course,we mainly concentrate on the least-squares(LS)error criterion The estimation of all-pole(AP)model leads to linear optimization problems,which is what we like. The estimation of all-zero(AZ)and PZ models requires the solutions to nonlinear optimization problems,which is generally troublesome. 9
9 In our course, we mainly concentrate on the least-squares (LS) error criterion • The estimation of all-pole (AP) model leads to linear optimization problems, which is what we like. • The estimation of all-zero (AZ) and PZ models requires the solutions to nonlinear optimization problems, which is generally troublesome. Model Estimation

Model Validation The goal of the model validation process is to find out whether the model O Agrees sufficiently with the observed data ●Describes the“true”signal generation system But how to validate the model? Key idea:Check whether the residual process,which is generated by the inverse of the fitted model,is a realization of white noise. 10
10 The goal of the model validation process is to find out whether the model ● Agrees sufficiently with the observed data ● Describes the “true” signal generation system But how to validate the model? Key idea: Check whether the residual process, which is generated by the inverse of the fitted model, is a realization of white noise. Model Validation

Model Validation The whiteness of the residual signal can be checked by the following statistical techniques Autocorrelation test(自相关检测) Power spectrum density test(功率谱密度检测) Partial autocorrelation test(部分自相关检测)
11 •Autocorrelation test(自相关检测) •Power spectrum density test(功率谱密度检测) •Partial autocorrelation test (部分自相关检测) The whiteness of the residual signal can be checked by the following statistical techniques Model Validation