
知识点回顾 1.最大功率传输条件 ·若负载阻抗中,电阻、电抗可独立变化,最大功率传输 条件为“共轭匹配”: Z=Zs ·若仅模值可变, 阻抗角不变,最大功率传输条件为“模 匹配”: IZHZ、I 思考:若负载为纯电阻呢? 依旧为模匹配! →IZ曰Z→RZI
知识点回顾 1. 最大功率传输条件 • 若负载阻抗中,电阻、电抗可独立变化,最大功率传输 条件为“共轭匹配” : • 若仅模值可变,阻抗角不变,最大功率传输条件为“模 匹配” : Z Z L S = | | | | Z Z L S = 思考:若负载为纯电阻呢? 依旧为模匹配! | | | | | | ZL = → ZS RL S = Z

知识点回顾 2.多频激励下有功功率如何计算? P=ap i=1 P,为第个频率分量激励产生的平均功率 ☆结论:多个不同频率(各频率之比为有理数)的正弦波产 生的总平均功率=各频率正弦量单独作用时所产生的平均 功率之和
知识点回顾 2. 多频激励下有功功率如何计算? ☆结论: 多个不同频率(各频率之比为有理数)的正弦波产 生的总平均功率=各频率正弦量单独作用时所产生的平均 功率之和。 1 N i i i P P P i = = å 为第 个频率分量激励产生的平均功率

知识点回顾 3.耦合电感耦合系数及VARk= 2.21= VΦΦ22VL M→M=kV☑L 41=±L di±M di, 当端口电压、电流取关联参考 dt 方向时,自感电压项前取“+” di 当端口电压、电流取非关联参 42=±L2 土M 考方向时,自感电压项前取” 当两电流同时从同名端流入时,互感电压项前和自感电压项前同号 当两电流同时从异名端流入时,互感电压项前和自感电压项前异号
知识点回顾 3.耦合电感耦合系数及VAR 12 21 11 22 2 1 1 2 M k L L M k L L = • = → = t i M t i u L t i M t i u L d d d d d d d d 2 1 2 2 1 2 1 1 = = 当两电流同时从同名端流入时,互感电压项前和自感电压项前同号 当两电流同时从异名端流入时,互感电压项前和自感电压项前异号 当端口电压、电流取关联参考 方向时,自感电压项前取“+” 当端口电压、电流取非关联参 考方向时,自感电压项前取“-
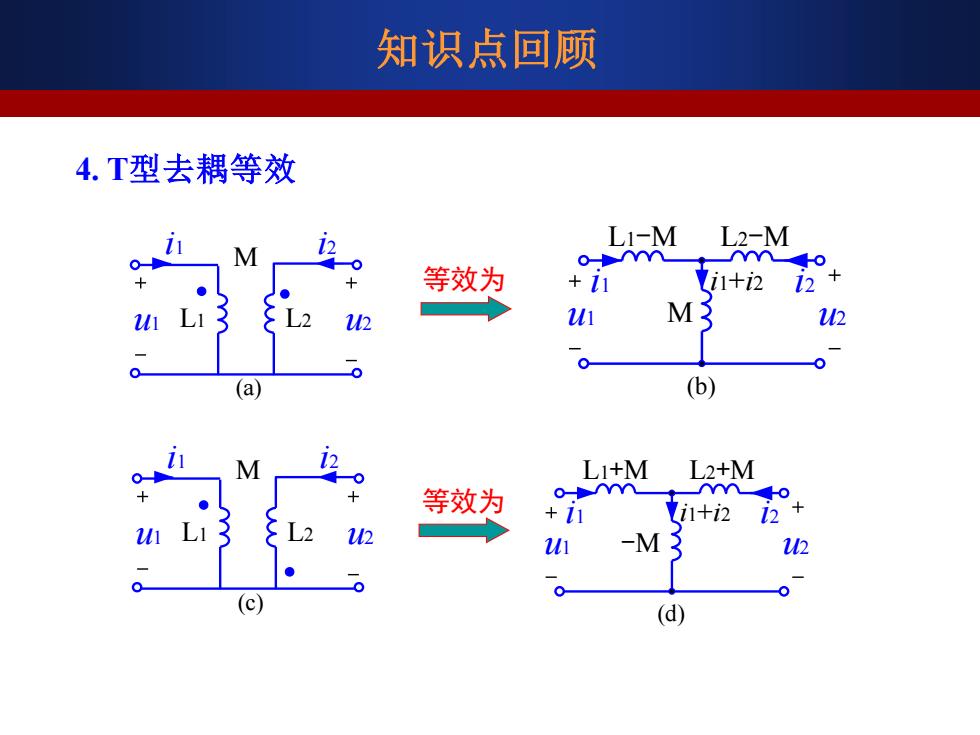
知识点回顾 4.T型去耦等效 LI-M L2-M 等效为 i1+2 M 12 (b) LI+M L2+M 等效为 +1 i1+i212 -M 12 (d)
知识点回顾 4. T型去耦等效 u2 M u1 L1 L2 i1 i2 (a) i1 i2 L1-M L2-M u1 M u2 (b) 等效为 i1+i2 u2 M u1 L1 L2 i1 i2 (c) 等效为 i1 i2 L1+M L2+M u1 -M u2 (d) i1+i2

4.6互感耦合电路 三、去耦等效电路 M =1H 2H 4H 6H 10H 6H =2H 2H 3H1
2H 6H 4.6 互感耦合电路 三、去耦等效电路 4H
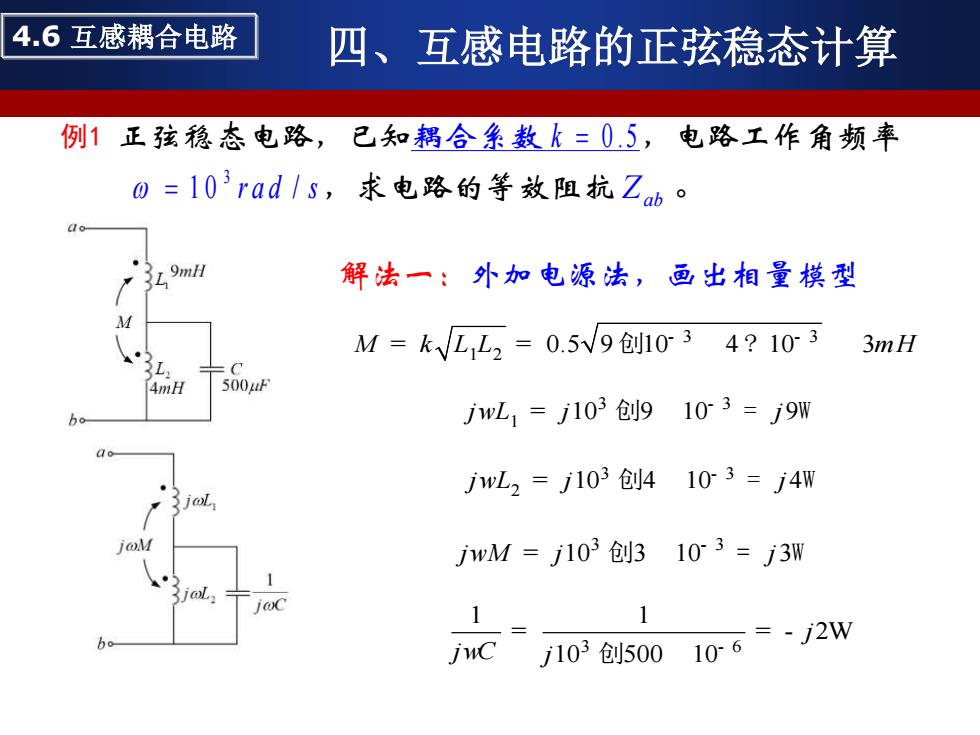
4.6互感耦合电路 四、互感电路的正弦稳态计算 例1正孩稳态电路,己知耦合华数k=0.5,电路工作角频率 0=103rad/s,求电路的等效阻抗Zb。 3红9mH 解法一:外加电源法,画出相量模型 M M=kLL2=0.5V9创1034?103 3mH L: 4mH 500F jwL1=j103创9103=j9w jwL2=j103创4103=j4W wM=j103创3103=3w 、1 jnC 103创500106=2W
例1 正弦稳态电路,已知耦合系数 ,电路工作角频率 ,求电路的等效阻抗 。 k = 0 .5 1 0 r a d / s 3 = Zab 3 3 1 2 M k L L mH 0.5 9 10 4 10 3 - - = = 创 ? 3 3 1 j L j j w 10 9 10 9 - = 创 = W 3 3 2 j L j j w 10 4 10 4 - = 创 = W 3 3 j M j j w 10 3 10 3 - = 创 = W 3 6 1 1 2 10 500 10 j j Cw j - = = - W 创 解法一:外加电源法,画出相量模型 4.6 互感耦合电路 四、互感电路的正弦稳态计算

4.6互感耦合电路 四、互感电路的正弦稳态计算 若在ab端外如电流源】,设端电压为U (注意:关联参考方向,同名端流入) ● joL 贩 贩 U=(jwL I+jwM 12)+(jwL2 12+jwMI) 贩 jwal+wMI= 贩 -12) C 代入元件值,消去1,整理后得: 0=-5.5j1 U Z ab= -5.5j2
若在 端外加电流源 ,设端电压为 (注意:关联参考方向,同名端流入) ab • I • U 1 2 2 2 U j L I j M I j L I j M I ( ) ( ) w w w w 贩 贩 ? = + + + 2 2 2 1 j L I j M I I I ( ) j C w w w 贩 贩 + = - 代入元件值,消去 整理后得: • • U = −5.5 j I = • = − • j I U Z ab 5.5 • 2 I 4.6 互感耦合电路 四、互感电路的正弦稳态计算
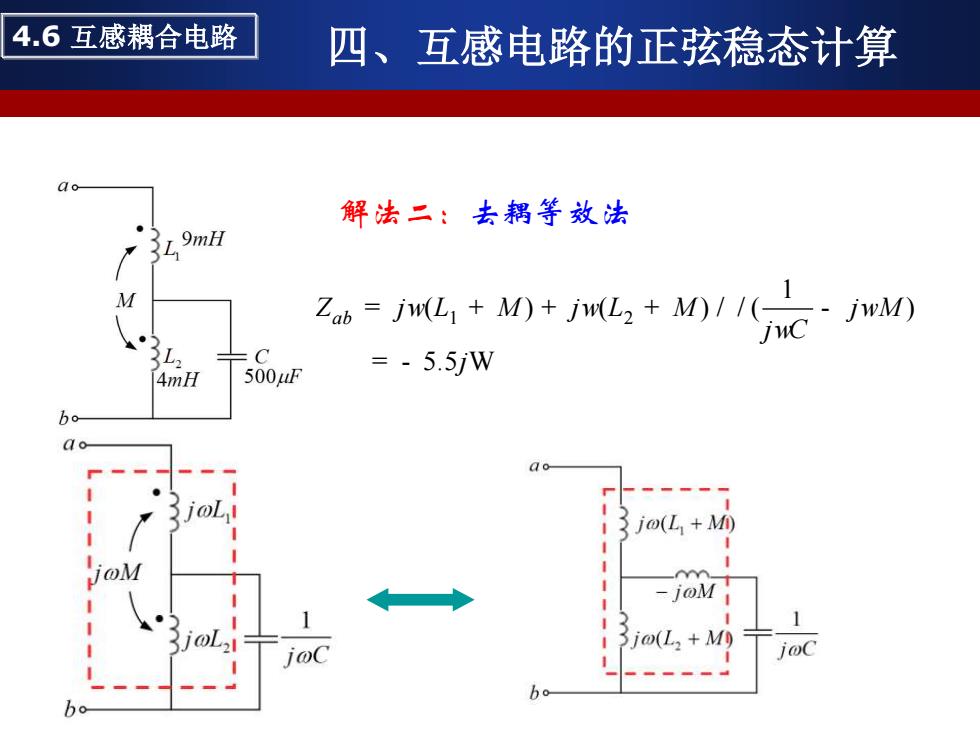
4.6互感耦合电路 四、互感电路的正弦稳态计算 解法二:去耦等效法 乙=jw4+M0+JL,+M)1C 3L2 4mH 500uF =-5.5W bo d o jo(L M) 0M j@(L2+M0 bo
解法二:去耦等效法 1 2 1 ( ) ( ) / / ( ) 5.5 ab Z j L M j L M j M j C j w w w w = + + + - = - W 4.6 互感耦合电路 四、互感电路的正弦稳态计算
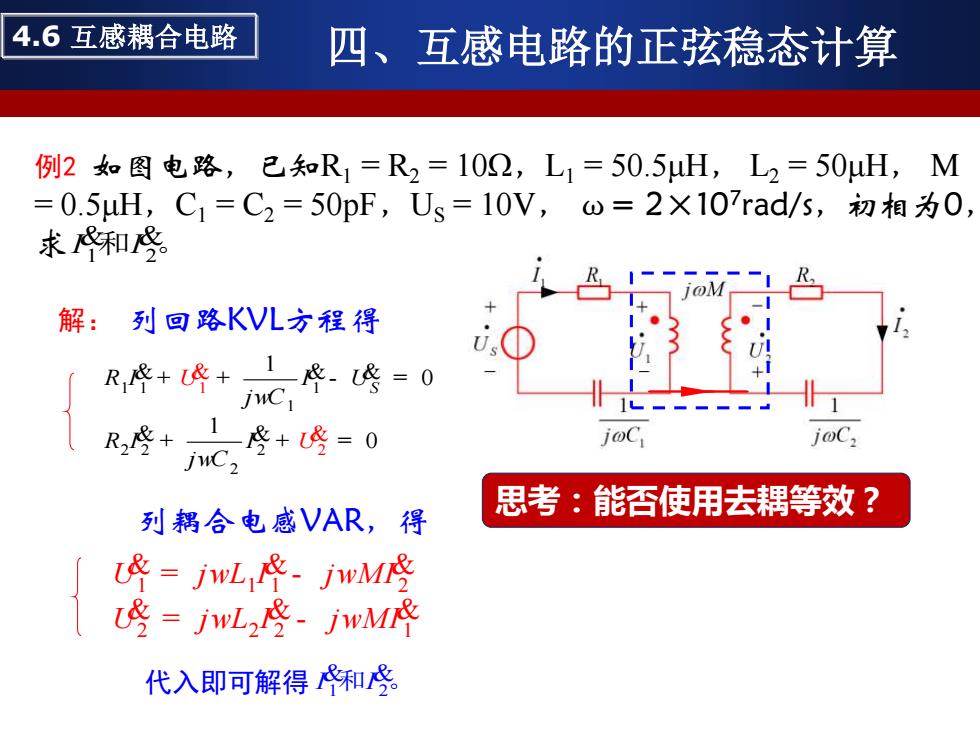
4.6互感耦合电路 四、互感电路的正弦稳态计算 例2如图电路,已知R1=R2=102,L1=50.5uH,L2=50uH,M =0.5uH,C1=C2=50pF,Us=10V,ω=2×107rad/s,初相为0, 求和及。 解:列回路KV儿方程得 R++G修=0 R,及+座+咚=0 joC joC 列耦合电感VAR,得 思考:能否使用去耦等效? =jwL,代.M =wL,空.jM 代入即可解得和
解: 列回路KVL方程得 1 1 2 2 1 1 1 2 2 2 1 0 1 0 R I I US j C R I I j C U U w w + + - = + + = & & & & & & & 列耦合电感VAR,得 1 1 1 2 2 2 2 1 U j L I j MI U j L I j MI w w w w = - = - & & & & & & 例2 如图电路,已知R1 = R2 = 10Ω,L1 = 50.5μH, L2 = 50μH, M = 0.5μH,C1 = C2 = 50pF,US = 10V, ω= 2×107 rad/s,初相为0, 求 1 2 I I & & 和 。 代入即可解得 1 2 I I & & 和 。 4.6 互感耦合电路 四、互感电路的正弦稳态计算 思考:能否使用去耦等效?

4.6互感耦合电路 四、互感电路的正弦稳态计算 例3如图电路的相量模型,已知Us=4V,求理想电压表的读数。 ,2 j12 解:设电流,和i,如图所标(关联 + 十同名端流入) =0 01j293 j4Q02 根据互感的VAR,有=jwL,代j2 由KV儿有=2+=(2+j2) 代 2+j2 在次级线图,由互感的VAR,有=mM-I?度= 2+2 取模得 -4 =√2V 2N2 W2 这个方法太费劲!去耦合更简单!
例3 如图电路的相量模型,已知US = 4V,求理想电压表的读数。 2 I& = 0 根据互感的VAR,有 1 1 1 1 U j L I j I & & & = w = 2 由KVL有 1 1 1 2 (2 2) S U I j & & & = + = + U& I 1 2 2 US I j = + & & 在次级线圈,由互感的VAR,有 2 1 1 1 1 2 2 S j U j U j j wMI I ´ = = ? = + & & & & 取模得 2 4 2 V 2 2 2 2 US U === 这个方法太费劲!去耦合更简单! 解:设电流 如图所标(关联 +同名端流入) 1 2 I I 和 4.6 互感耦合电路 四、互感电路的正弦稳态计算