2.7 等效电源定理 一、 等效电源定理 1、戴维南定理:任意一个线性二端含源电路,对其外部 而言,可以用一个电压源和电阻的串联组合来等效。 开 a 路 任意 N Woc 二端 任何 可等效为2uoc 任何 线性 u 外接 外接 6 Ro 电路N 电路 电路 a 含源 No 戴维南等效电 所有独立源为 b 路 零值 戴维南等效内阻
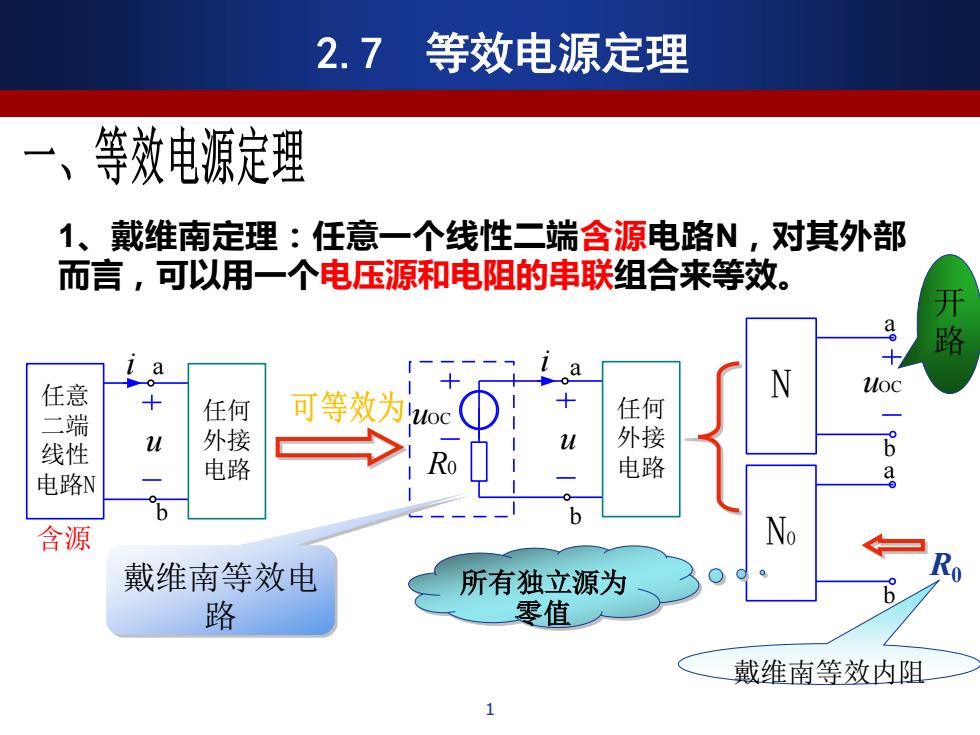
u 任意 二端 线性 电路N 任何 外接 电路 i a b b u 任何 外接 电路 i uOC R0 a N uOC a b N0 a b 所有独立源为 R0 零值 开 路 戴维南等效电 路 戴维南等效内阻 1、戴维南定理:任意一个线性二端含源电路N,对其外部 而言,可以用一个电压源和电阻的串联组合来等效。 2.7 等效电源定理 1 含源

2.7等效电源定理 三、戴维南等效内阻的计算★ ·1、对无受控源的二端电路N一串并联方法 若二端电路N中无受控源,当令N中所有独立源的值为 零(电压源短路,电流源开路)后,而得到的N是一个纯 电阻电路。此时,利用电阻的串并联公式和Y-△等效公式 求R最简单。 2
2 2.7 等效电源定理 三、戴维南等效内阻的计算★ ❖1、对无受控源的二端电路N——串并联方法 若二端电路N中无受控源,当令N中所有独立源的值为 零(电压源短路,电流源开路)后,而得到的N0是一个纯 电阻电路。此时,利用电阻的串并联公式和Y-△等效公式 求R0最简单
2.7等效电源定理 三、戴维南等效内阻的计算★ ·2、对于含受控源的二端电路N 冬(1)外加电源法★ 所有独立源的值为零(电压源短路,电流源开路); 保留受控源; No u Ro No No (a)外加电压源法 (b)外加电流源法 u与i对N一定要取 关联方向呦】
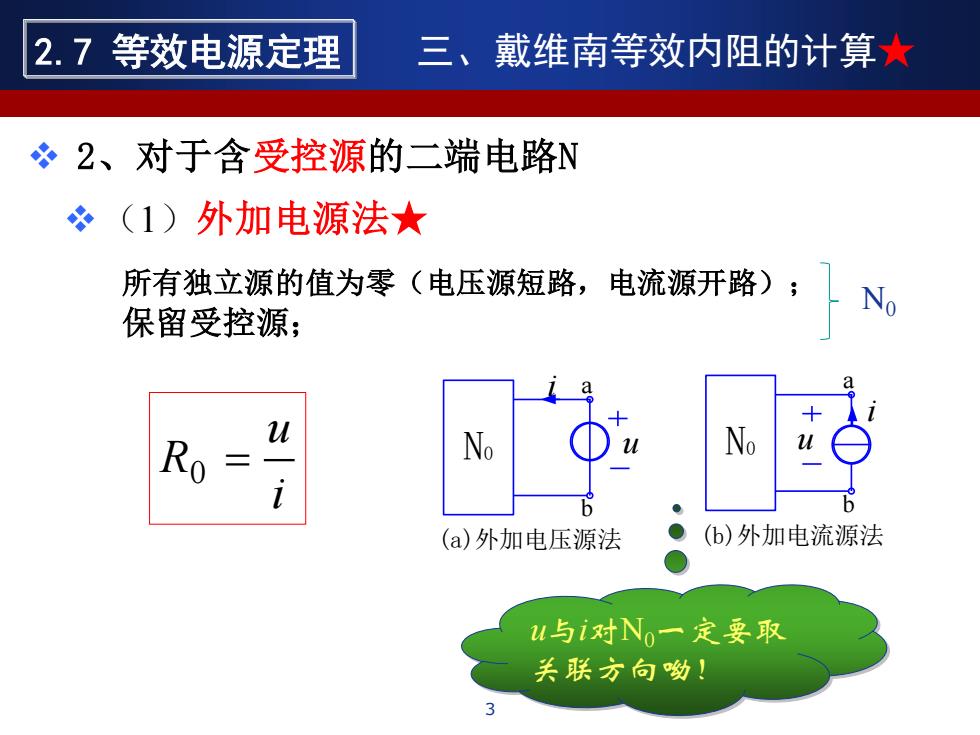
所有独立源的值为零(电压源短路,电流源开路); 保留受控源; N0 u a b i (a)外加电压源法 N0 u a b i (b)外加电流源法 i u R0 = u与i对N0一定要取 关联方向呦! ❖(1)外加电源法★ ❖ 2、对于含受控源的二端电路N 3 2.7 等效电源定理 三、戴维南等效内阻的计算★ N0

2.7等效电源定理 三、戴维南等效内阻的计算★ (2)开路短路法 先求出oc,再求出isc(注意:若求uoc时其参考 方向a为“+”极,则求isc时其参考方向应设成从a 流向b),则 R0= uoc isc
先求出uOC,再求出iSC(注意:若求uOC时其参考 方向a为“+”极,则求iSC时其参考方向应设成从a 流向b),则 ❖ (2)开路短路法 4 SC OC i u R0 = 2.7 等效电源定理 三、戴维南等效内阻的计算★

2.7等效电源定理 三、戴维南等效内阻的计算★ ,(3)伏安关系法 戴维南等效电路如图(a),端口上电压u与电 流取关联参考方向,其端口的伏安关系(VAR) 为 u=uoc RoI 拓展:非关联(将i反向)u=uoc-R,I (a) 所谓伏安关系法就是直接对二端线性电路N,推导出两端子 上的电压和电流之间的一次关系式,其常数项即为开路电压 4oc,电流前面所乘的系数即为等效内阻R,。 思考:若未接入外电路,电流=0,u=uoc,无法测内阻,方法失效」 因此,若要使用伏安关系法,必须接入外电路。最简单方法:外接激励源!
戴维南等效电路如图(a),端口上电压u与电 流i取关联参考方向,其端口的伏安关系(VAR) 为 u = uOC + R0 I 拓展:非关联(将i反向) u = uOC - R0 I b u (a) i R0 a uOC 所谓伏安关系法就是直接对二端线性电路N,推导出两端子 上的电压u和电流i之间的一次关系式,其常数项即为开路电压 uOC ,电流前面所乘的系数即为等效内阻R0 。 ❖ (3)伏安关系法 5 2.7 等效电源定理 三、戴维南等效内阻的计算★ 思考:若未接入外电路,电流i=0,u=uOC,无法测内阻,方法失效! 因此,若要使用伏安关系法,必须接入外电路。最简单方法:外接激励源!

2.7等效电源定理 三、戴维南等效内阻的计算★ 总结 1.外加电源法:将内部激励源全部置零,可简化内 部电路,利于分析; 2.开路短路法:一次性解决激励源取值和等效内阻 取值 3.伏安关系法:适合工程实践!原因:不易烧毁电 源,也避免了外加电源的内阻问题。 4.上述三种方法,也能用于纯电阻情形!
6 2.7 等效电源定理 三、戴维南等效内阻的计算★ 总结 1. 外加电源法:将内部激励源全部置零,可简化内 部电路,利于分析; 2. 开路短路法:一次性解决激励源取值和等效内阻 取值 3. 伏安关系法:适合工程实践!原因:不易烧毁电 源,也避免了外加电源的内阻问题。 4. 上述三种方法,也能用于纯电阻情形!
2.7等效电源定理 四、应用举例 例:如图(a)所示电路,已知当R=92时I=0.4A,若R变为72 时,其上的电流又为多大?(Us,s未知!oC,isc无法求!) 解:(1)求R。 将图(a)中电压源短路,电流源开路得 到No,并外加电流源I,如图(b)所示。 由KCL得I=3L1-I,则1=0.5I 由KVL和OL列A回路方程为 D U=2I-2I1=2I-2×0.5I=I 所以R=UI=12 (a 22 22 (2)画出戴维南等效电路,并接上 R,得图(c)电路。由该电路得 Uoc_ Uoc Ro+RL 1+RL (b) 代入已知条件,么==04 1+9 ,解得Uoc=4V 3)将R=72代入上式,得出相应的电流1=4/1+7)=0.5A
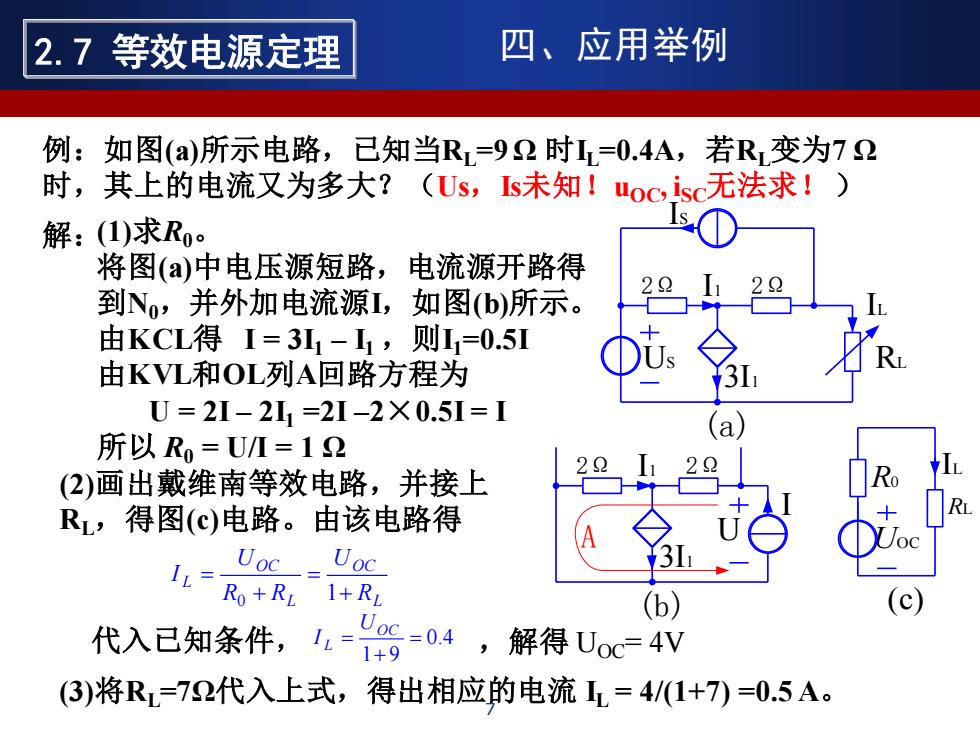
例:如图(a)所示电路,已知当RL=9 Ω 时IL=0.4A,若RL变为7 Ω 时,其上的电流又为多大?(Us,Is未知!uOC, iSC无法求! ) 解:(1)求R0。 将图(a)中电压源短路,电流源开路得 到N0,并外加电流源I,如图(b)所示。 由KCL得 I = 3I1 – I1 ,则I1=0.5I 由KVL和OL列A回路方程为 U = 2I – 2I1 =2I –2×0.5I = I 所以 R0 = U/I = 1 Ω (2)画出戴维南等效电路,并接上 RL,得图(c)电路。由该电路得 L OC L OC L R U R R U I + = + = 1 0 (3)将RL=7Ω代入上式,得出相应的电流 IL = 4/(1+7) =0.5 A。 代入已知条件, 0.4 1 9 = + = OC L U I ,解得 UOC= 4V 2Ω I1 2Ω IS US 3I1 IL RL (a) 2Ω I1 2Ω 3I1 I (b) A U RL IL UOC R0 (c) 7 2.7 等效电源定理 四、应用举例
2.7等效电源定理 四、应用举例 例:如图所示电路中,N为线性含源单口网络。已知:u=2000i+10 ();is=2mA,求N的等效电路(注意:N的端口由该VAR描述 吗?)。 解:依据戴维南定理,原电路N可 等效为戴维南等效电路,如图(b)。 电路的VAR方程为: N u=R(i+is)+us =Ri+2×10R+us 由于已知:u=2000i+10,所以 R=20002, 2×10-3R+s=10 解得:R=20002;s=6V 8
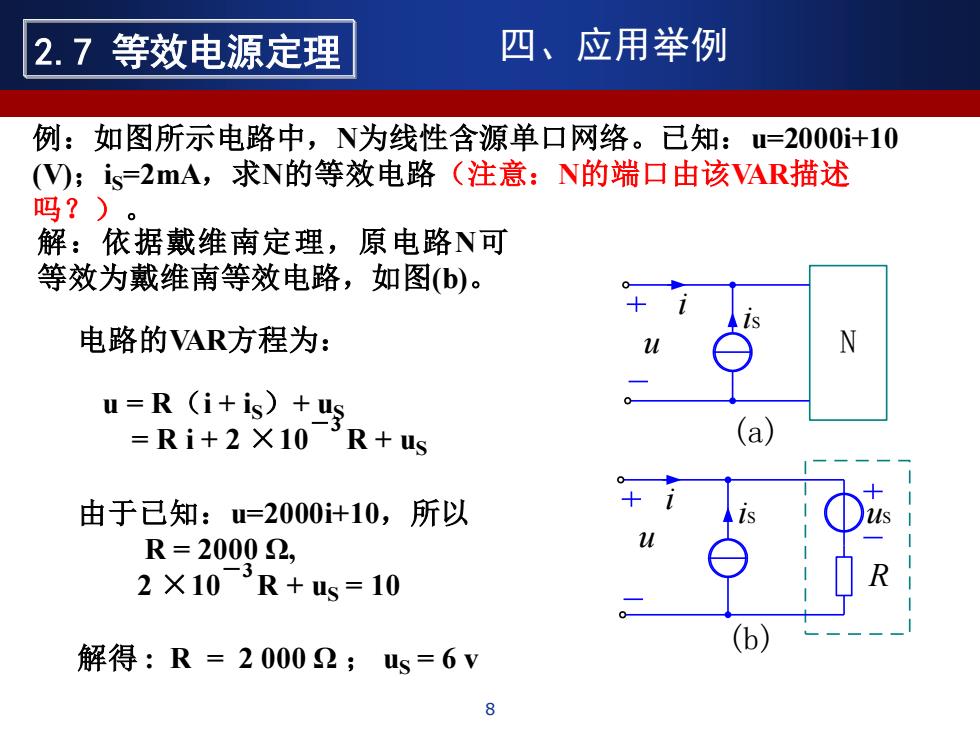
例:如图所示电路中,N为线性含源单口网络。已知:u=2000i+10 (V);iS=2mA,求N的等效电路(注意:N的端口由该VAR描述 吗?)。 解:依据戴维南定理,原电路N可 等效为戴维南等效电路,如图(b)。 电路的VAR方程为: u = R(i + iS)+ uS = R i + 2 ×10-3 R + uS 由于已知:u=2000i+10,所以 R = 2000 Ω, 2 ×10-3 R + uS = 10 解得 : R = 2 000 Ω ; uS = 6 v i u iS (a) N i u iS (b) uS R 8 2.7 等效电源定理 四、应用举例
2.7等效电源定理 六、最大功率传输定理 1、最大功率传输条件(最大功率匹配定理): 实际中,常遇到这样的问题:给定一个有源 二端电路,向一负载电阻R供电。问R为何值 的电 R 时其上获得最大功率? 路N (a) 由于电路N给定,因此可将其等效成戴维南 等效电路,如图(b)所示。由该图可知,负载RL 消耗的功率为 Ro uoc PL=iRL-Ro+RL R
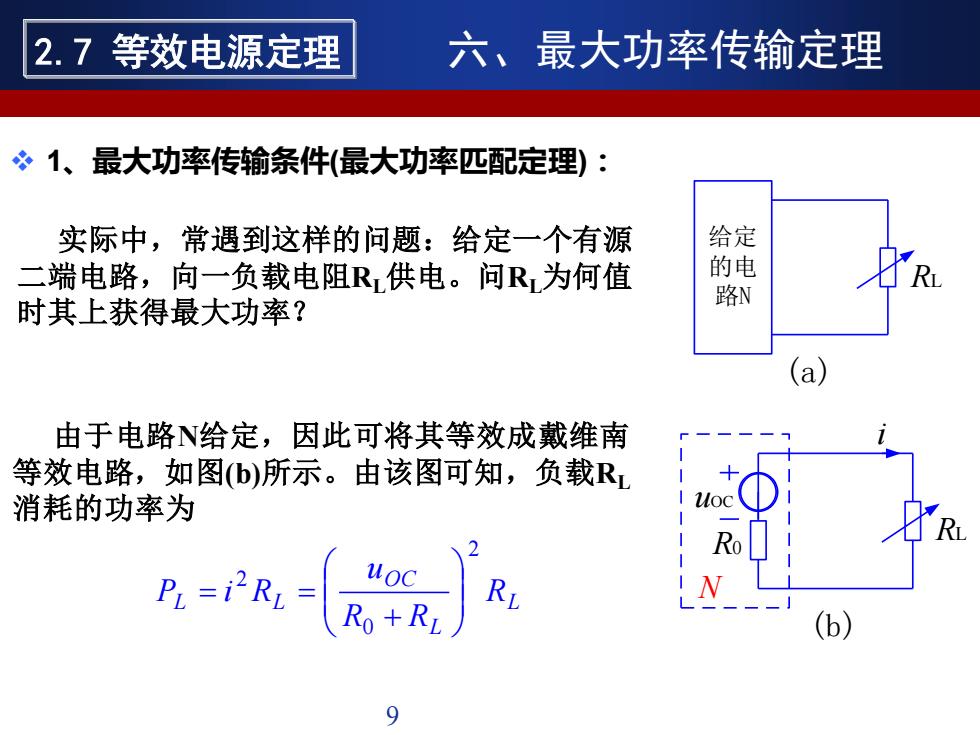
实际中,常遇到这样的问题:给定一个有源 二端电路,向一负载电阻RL供电。问RL为何值 时其上获得最大功率? (a) 给定 的电 路N RL 由于电路N给定,因此可将其等效成戴维南 等效电路,如图(b)所示。由该图可知,负载RL 消耗的功率为 (b) RL uOC R0 N i 9 ❖ 1、最大功率传输条件(最大功率匹配定理): 六、最大功率传输定理 L L OC L L R R R u P i R 2 0 2 + = = 2.7 等效电源定理

2.7等效电源定理 六、最大功率传输定理 为求出功率最大的条件,求P对R的导数,并令它等于零,即 dPL=cl【R,+R}-2R,(R+R〗_6c(Ro-R 2=0 dRL (R+R)4 (R。+R)3 解得RL=R,又由于B dR R,=R, <0 8R 所以,当R=R时负载获得的功率最大。功率的最大值为 PL max 4R0 R=R也称为最大功率匹配条件 10
为求出功率最大的条件,求PL对RL的导数,并令它等于零,即 所以,当RL = R0时负载获得的功率最大。功率的最大值为 RL = R0也称为最大功率匹配条件 解得RL = R0,又由于 2 max 0 4 OC L u P R = 10 2 2 2 0 0 4 3 0 0 0 [( ) 2 ( )] 0 ( ( ) ) ( ) L OC L L L OC L L L L dP u R R R R R u d R R R R R R R + - + = = = + + - 0 2 2 2 3 0 0 8 L L OC R R L d P u dR R = = - < 2.7 等效电源定理 六、最大功率传输定理