2.5齐次定理和叠加定理 、齐次定理 1、基本内容:对于具有唯一解的线性电路,当只有一个激 励源(独立电压源或独立电流源)作用时,其响应(电路任 意处的电压或电流)与激励成正比。 响应∝激励 N N 不含 不含 独立源 独立源 (a) (b) 。=Ks(常量K单位为S) i。=Kis(常量K3无单位) 4。=K2s(常量K无单位) u。=Ks(常量K4单位为2) 1
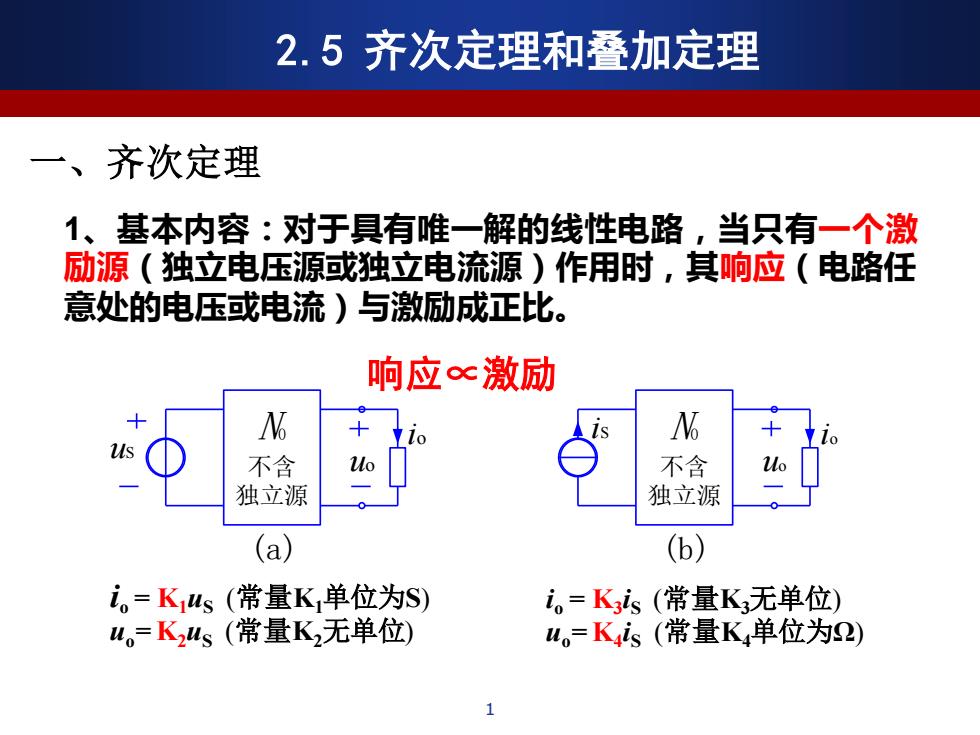
uS (a) N0 不含 独立源 uo io iS (b) N0 不含 独立源 uo io io = K1uS (常量K1单位为S) uo= K2uS (常量K2无单位) io = K3 iS (常量K3无单位) uo= K4 iS (常量K4单位为Ω) 1、基本内容:对于具有唯一解的线性电路,当只有一个激 励源(独立电压源或独立电流源)作用时,其响应(电路任 意处的电压或电流)与激励成正比。 2.5 齐次定理和叠加定理 一、齐次定理 1 响应∝激励

2.5齐次定理和叠加定理 二、叠加定理 二、叠加定理 1、基本内容: 对于具有唯一解的线性电路,多个激励源共同作用时引起 的响应(电路中各处的电流、电压)等于各个激励源单独作 用时(其它激励源的值置零)所引起的响应之和
1、基本内容: 对于具有唯一解的线性电路,多个激励源共同作用时引起 的响应(电路中各处的电流、电压)等于各个激励源单独作 用时(其它激励源的值置零)所引起的响应之和。 二、叠加定理 2 2.5 齐次定理和叠加定理 二、叠加定理
2.6替代定理 一、替代定理 1、基本内容:对于具有唯一解的线性或非线性电路,若某支路 的电压或电流已知,则该支路可用方向和大小与“相同的电压源 替代,或用方向和大小与相同的电流源替代,而不会影响其它各 处的电流和电压。 若已知A支路电压u N 1s=1 N 若已知A支路电流i 支路A用电压源或电流源替代后,NI中的电流、电压保持不变
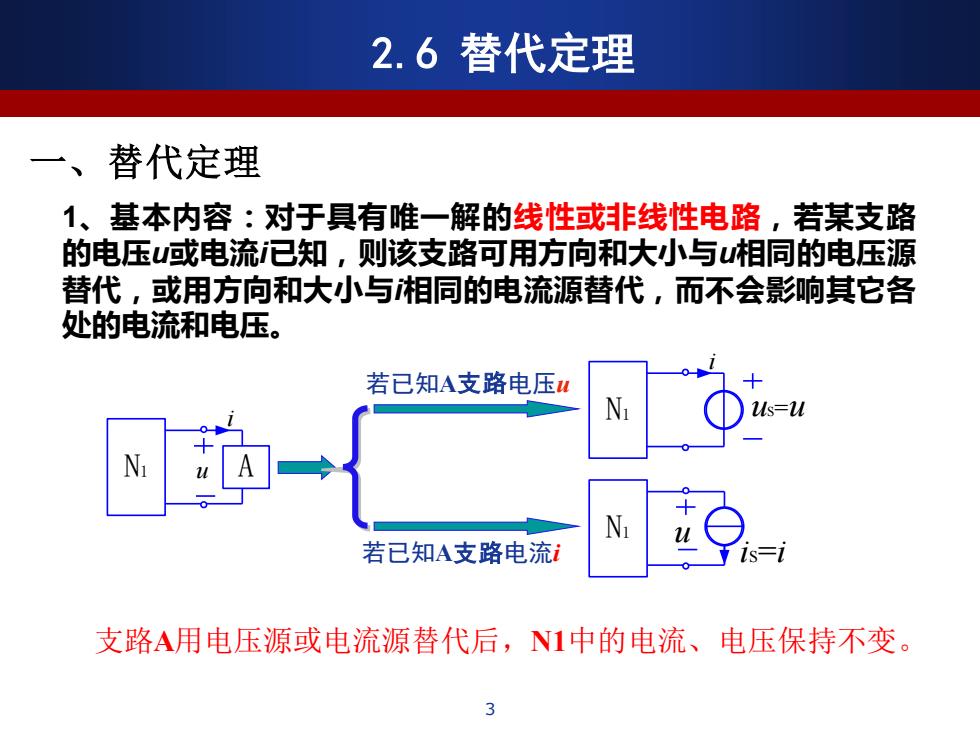
若已知A支路电压u 若已知A支路电流i N1 u A i N1 uS=u i N1 u iS=i 支路A用电压源或电流源替代后,N1中的电流、电压保持不变。 1、基本内容:对于具有唯一解的线性或非线性电路,若某支路 的电压u或电流i已知,则该支路可用方向和大小与u相同的电压源 替代,或用方向和大小与i相同的电流源替代,而不会影响其它各 处的电流和电压。 2.6 替代定理 3 一、替代定理
2.7 等效电源定理 一、 等效电源定理 1、戴维南定理:任意一个线性二端含源电路N,对其外部 而言,可以用一个电压源和电阻的串联组合来等效。 开 a 路 任意 Woc 二端 任何 可等效为2uoc N 任何 线性 u 外接 外接 6 电路 Ro 电路N 电路 a 含源 No 戴维南等效电 所有独立源为 6 路 零值 戴维南等效内阻
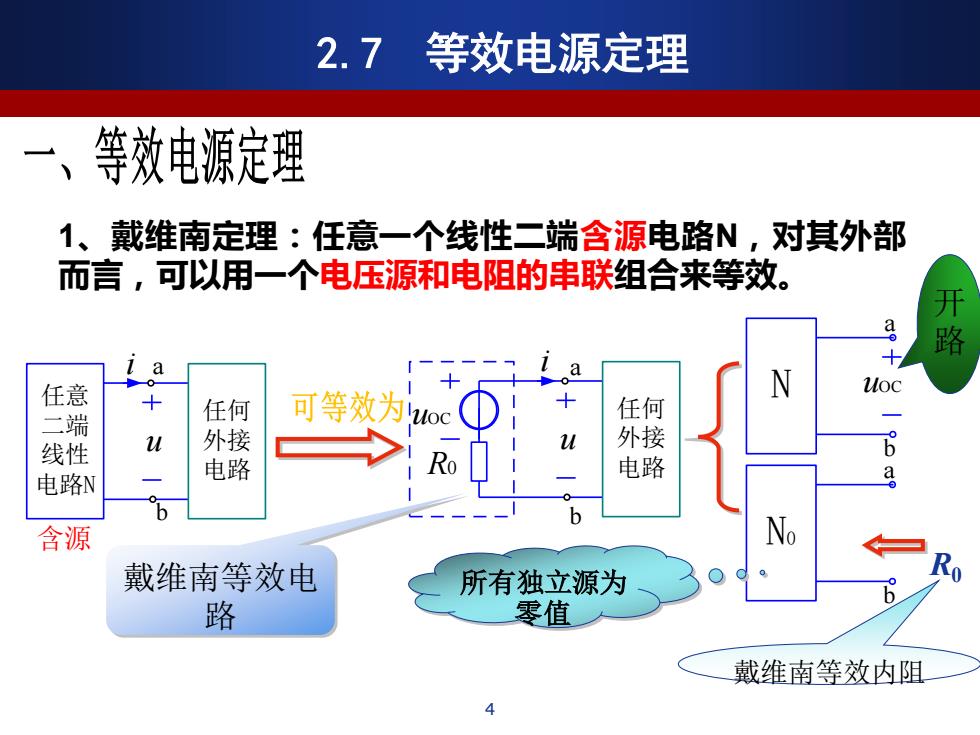
u 任意 二端 线性 电路N 任何 外接 电路 i a b b u 任何 外接 电路 i uOC R0 a N uOC a b N0 a b 所有独立源为 R0 零值 开 路 戴维南等效电 路 戴维南等效内阻 1、戴维南定理:任意一个线性二端含源电路N,对其外部 而言,可以用一个电压源和电阻的串联组合来等效。 2.7 等效电源定理 4 含源
2.7 等效电源定理 等效电源定理 2、诺顿定理:任意一个线性二端含源电路N,对其外部而言 1 可以用一个电流源和电阻的并联组合来等效。 a a 注意电流 任意 二端 任何 可 等效为sc 任何 N 线性 u 外接 外接 电路N 电路 电路 b a b 诺顿等效电路 No R0 注意电流源的方向 所有独立源为零值! 戴维南等效电路与诺顿等效电路本质上是相同 戴维南等效 的,两者互为等效。 内阻
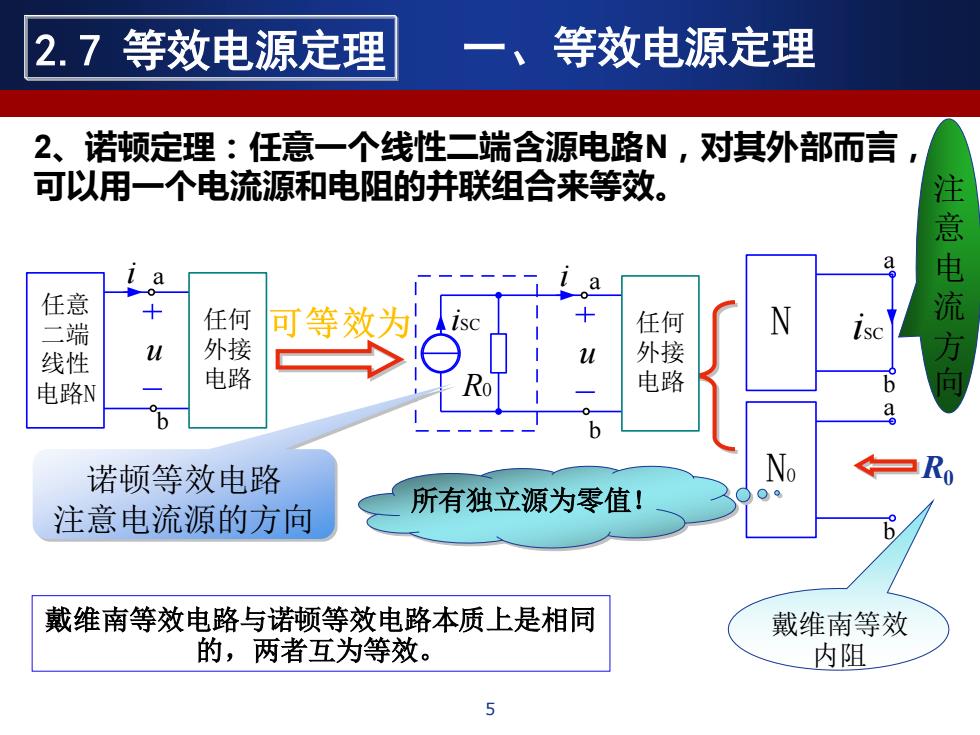
u 任意 二端 线性 电路N 任何 外接 电路 i a b N0 a b R0 所有独立源为零值! 注 意 电 流 方 向 b u 任何 外接 电路 i iSC R0 a N a b iSC 诺顿等效电路 注意电流源的方向 戴维南等效 内阻 戴维南等效电路与诺顿等效电路本质上是相同 的,两者互为等效。 2、诺顿定理:任意一个线性二端含源电路N,对其外部而言, 可以用一个电流源和电阻的并联组合来等效。 2.7 等效电源定理 一、等效电源定理 5
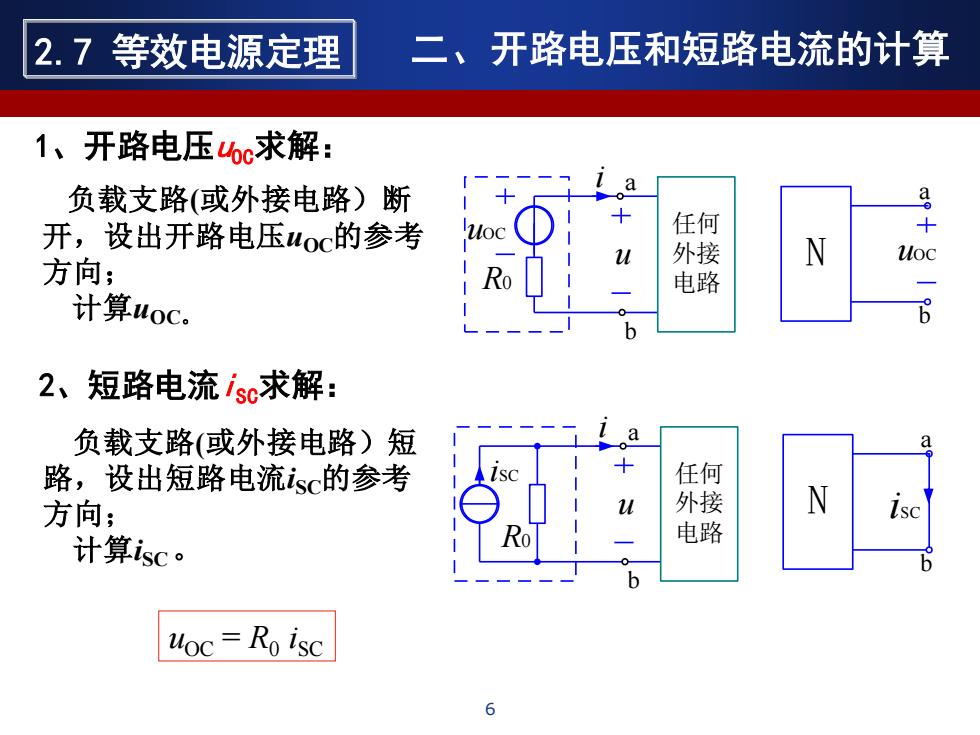
2.7等效电源定理 二、开路电压和短路电流的计算 1、 开路电压hc求解: 负载支路(或外接电路)断 开,设出开路电压uoc的参考 任何 M 外接 N 方向; Ro 电路 计算uoc。 2、短路电流isc求解: 负载支路(或外接电路)短 a 路,设出短路电流isc的参考 任何 方向; 外接 计算isc。 电路 uoc=Ro isc
负载支路(或外接电路)断 开,设出开路电压uOC的参考 方向; 计算uOC。 b u 任何 外接 电路 i uOC R0 a N uOC a b 2、短路电流iSC求解: 负载支路(或外接电路)短 路,设出短路电流iSC的参考 方向; 计算iSC。 b u 任何 外接 电路 i iSC R0 a N a b iSC uOC = R0 iSC 1、开路电压uOC求解: 二、开路电压和短路电流的计算 6 2.7 等效电源定理

2.7等效电源定理 三、戴维南等效内阻的计算★ %1、对无受控源的二端电路N一串并联方法 若二端电路N中无受控源,当令N中所有独立源的值为 零(电压源短路,电流源开路)后,而得到的N是一个纯 电阻电路。此时,利用电阻的串并联公式和Y-△等效公式 求R最简单
7 2.7 等效电源定理 三、戴维南等效内阻的计算★ ❖1、对无受控源的二端电路N——串并联方法 若二端电路N中无受控源,当令N中所有独立源的值为 零(电压源短路,电流源开路)后,而得到的N0是一个纯 电阻电路。此时,利用电阻的串并联公式和Y-△等效公式 求R0最简单
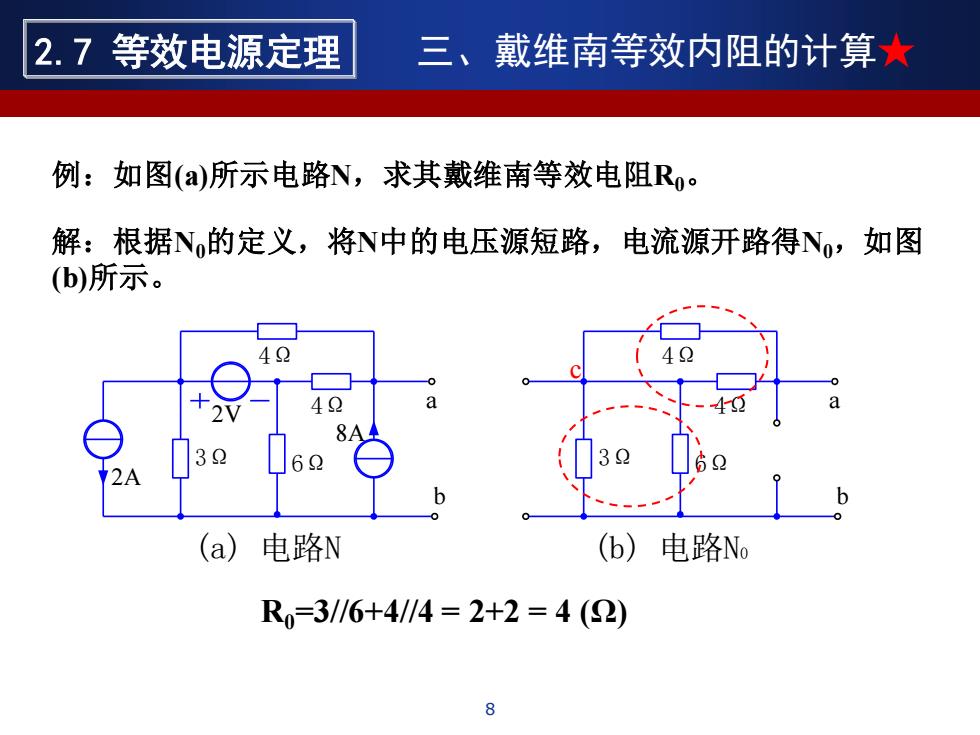
2.7等效电源定理 三、戴维南等效内阻的计算★ 例:如图(a)所示电路N,求其戴维南等效电阻Ro。 解:根据N的定义,将N中的电压源短路,电流源开路得No,如图 (b)所示。 4 42 a 32 62 2A a) 电路N (b) 电路No R=3/6+4/4=2+2=4(2)
例:如图(a)所示电路N,求其戴维南等效电阻R0。 2A 3Ω a b 6Ω 4Ω 8A 2V 4Ω (a) 电路N 解:根据N0的定义,将N中的电压源短路,电流源开路得N0,如图 (b)所示。 3Ω a b 6Ω 4Ω 4Ω (b) 电路N0 R0=3//6+4//4 = 2+2 = 4 (Ω) 8 2.7 等效电源定理 三、戴维南等效内阻的计算★ c
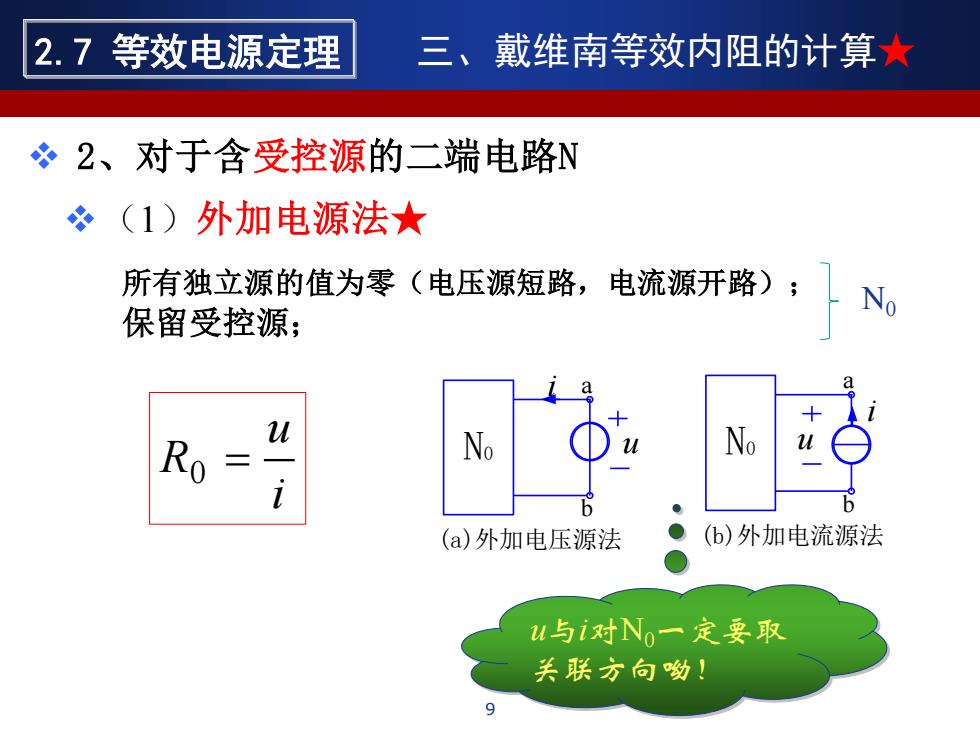
2.7等效电源定理 三、戴维南等效内阻的计算★ 2、对于含受控源的二端电路N 冬(1)外加电源法★ 所有独立源的值为零(电压源短路,电流源开路); No 保留受控源; Ro u No No (a)外加电压源法 (b)外加电流源法 u与i对N一定要取 关联方向呦】
所有独立源的值为零(电压源短路,电流源开路); 保留受控源; N0 u a b i (a)外加电压源法 N0 u a b i (b)外加电流源法 i u R0 = u与i对N0一定要取 关联方向呦! ❖(1)外加电源法★ ❖ 2、对于含受控源的二端电路N 9 2.7 等效电源定理 三、戴维南等效内阻的计算★ N0
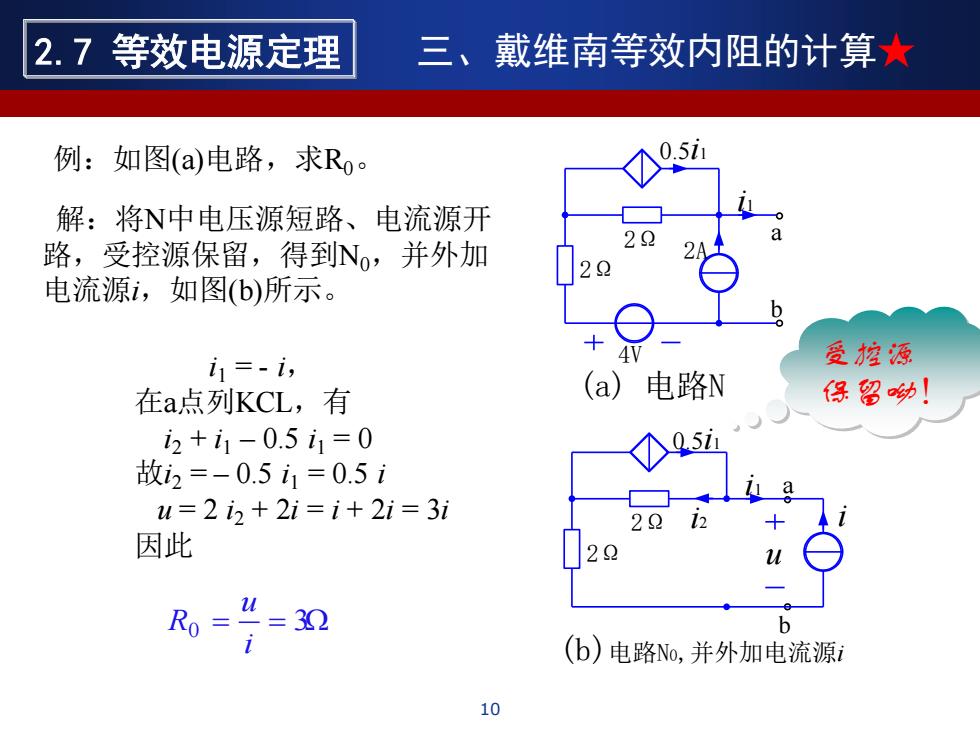
2.7等效电源定理 三、戴维南等效内阻的计算★ 例:如图(a)电路,求Ro。 0.5i1 解:将N中电压源短路、电流源开 路,受控源保留,得到No,并外加 22 电流源1,如图(b)所示。 i1=-i, 受控源 在a点列KCL,有 (a)电路N 保留呦! 2+i1-0.5i1=0 1个Q5i 故i2=-0.5i1=0.5i u=2i2+2i=i+2i=3i 22 因此 R0= =32 (b)电路No,并外加电流源i 10
例:如图(a)电路,求R0。 0.5i1 i1 2Ω a b 2Ω 4V 2A (a) 电路N i1 2Ω a b 2Ω (b)电路N0,并外加电流源i i u i2 0.5i1 解:将N中电压源短路、电流源开 路,受控源保留,得到N0,并外加 电流源i,如图(b)所示。 i1 = - i, 在a点列KCL,有 i2 + i1 – 0.5 i1 = 0 故i2 = – 0.5 i1 = 0.5 i u = 2 i2 + 2i = i + 2i = 3i 因此 0 = = 3Ω i u R 受控源 保留呦! 10 2.7 等效电源定理 三、戴维南等效内阻的计算★