
知识点回顾 1.直流激励一阶电路的快速求解方法 三要素法:不用列微分方程求解,只需要求得初始值、稳态值、时常数三要素! y(t)=y(0,)-y(伴)I+y(¥) =y(0,e/+y(¥)1-e1) 2.如何计算三要素? ·初始值y(0+):(1)先计算uc0-)和(0-),换路定律得独立初始值uc(04) =uc(0-),i(0+)=i(0-);(2)画0+等效电路(独立源替换独立初始 值),求非独立初始值 ·稳态值y(o):换路后t→∞时,画等效电路(电容开路、电感短路), 电阻电路分析得稳态值 。 时常数T:一阶RC电路,T=RC,一阶RL电路τ=LR,R为换路后 戴维南等效内阻
知识点回顾 1. 直流激励一阶电路的快速求解方法 三要素法:不用列微分方程求解,只需要求得初始值、稳态值、时常数三要素! / / / ) (0 ) ( ) ( ) ( 0 ) ) ( [ ] ( )(1 t t t y y y y e e y y t e t - - t t + - + = - ¥ = ¥ - ¥ + + 2. 如何计算三要素? • 初始值 y (0+ ) :(1)先计算uC(0-)和iL (0-),换路定律得独立初始值uC(0+ ) = uC(0-), iL (0+ ) = iL (0-); (2)画0+等效电路(独立源替换独立初始 值),求非独立初始值 • 稳态值 y (∞) :换路后t→∞时,画等效电路(电容开路、电感短路), 电阻电路分析得稳态值 • 时常数 τ :一阶RC电路,τ = R0C,一阶RL电路τ = L /R0 ,R0为换路后 戴维南等效内阻

知识点回顾 3.三要素法可以用来求解哪些响应? ·全能! ·一切全响应、零输入响应(分量)、零状态响应(分量) 4.求解零输入/零状态响应(分量)时,需要注意什么? ·计算零输入响应时,恒有y(0)=0,无需计算稳态值,只需计算初始值和时 常数 ·计算零状态响应时,恒有uc(0)=0,i(0)=0,但可能仍需计算三要素!只 有所需初始值为独立初始值时,才无需计算初始值。 ·若电路由初始储能和独立源共同激励,计算初始值时须注意: 零状态响应分量初始值:独立初始值置零! 零输入响应分量初始值:外加独立源置零!
知识点回顾 3. 三要素法可以用来求解哪些响应? • 全能! • 一切全响应、零输入响应(分量)、零状态响应(分量) 4. 求解零输入/零状态响应(分量)时,需要注意什么? • 计算零输入响应时,恒有 y (∞) =0,无需计算稳态值,只需计算初始值和时 常数 • 计算零状态响应时,恒有 uC(0+ ) =0, iL(0+ ) =0,但可能仍需计算三要素!只 有所需初始值为独立初始值时,才无需计算初始值。 • 若电路由初始储能和独立源共同激励,计算初始值时须注意: 零状态响应分量初始值:独立初始值置零! 零输入响应分量初始值:外加独立源置零!
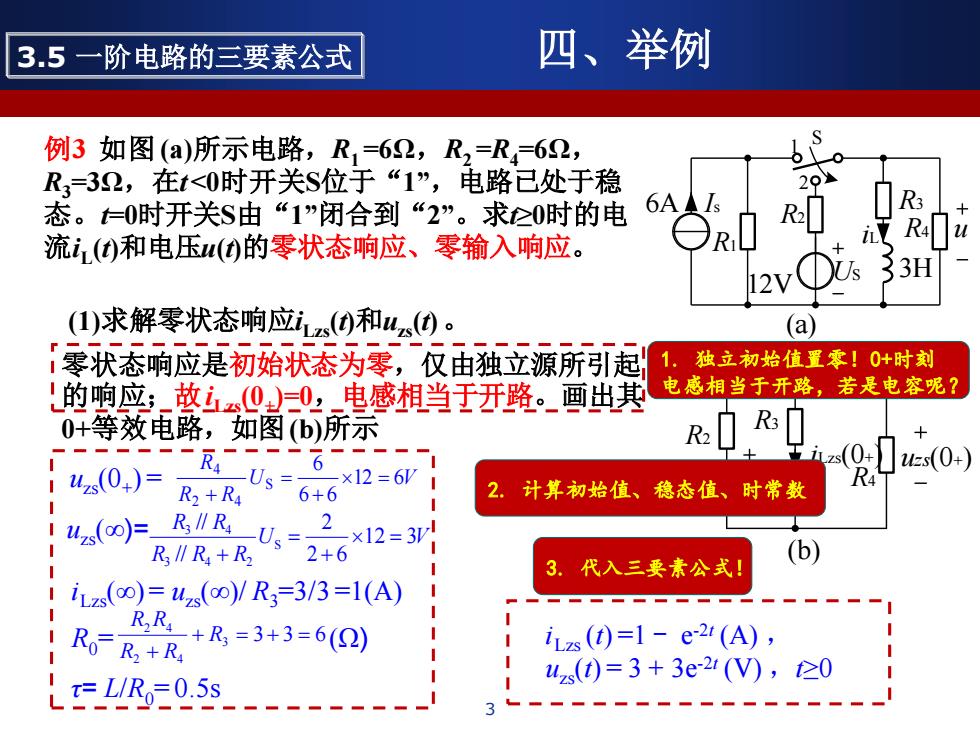
3.5一阶电路的三要素公式 四、举例 例3如图(a)所示电路,R1=62,R,=R=62, R3=32,在t<0时开关S位于“1”,电路已处于稳 b 204 态。=0时开关S由“1”闭合到“2”。求仑0时的电 6A5 流()和电压()的零状态响应、零输入响应。 R4 h2v①s 1 3H (I)求解零状态响应izs(和us(④。 (a) 「零状态响应是初始状态为零,仅由独立源所引起 1.独立初始值置零!0+时刻 L的响座:-憨⑨0电感相当于开路。画出其电感相当于开路,若是电容死? 0+等效电路,如图(b)所示 R3 1-二二一一r41_6 u0,)=R+R 6 us(0+) ×12=6i R4 6+6 2.计算初始值、稳态值、时常数 2 四月R/R26x2=3 R∥R+R2 3.代入三要素公式! (b) !iLz(oo)=u2s(o)/R3=3/3=1(A) CRR+R=3+3=6(Q) 1 RoR+R izs(0)=1-e2(A), L=☑R05s s0=3+3e2(V),0 3
3 3.5 一阶电路的三要素公式 四、举例 例3 如图 (a)所示电路,R1 =6Ω,R2 =R4=6Ω, R3=3Ω,在t <0时开关S位于“1”,电路已处于稳 态。t=0时开关S由“1”闭合到“2”。求t≥0时的电 流iL (t)和电压u(t)的零状态响应、零输入响应。 R2 6A Is US 12V 3H iL u S 1 2 (a) R1 R4 R3 (1)求解零状态响应iLzs(t)和uzs(t) 。 零状态响应是初始状态为零,仅由独立源所引起 的响应;故iLzs(0+ )=0,电感相当于开路。画出其 0+等效电路,如图(b)所示 R2 R4 R3 iLzs(0+) uzs(0+) (b) uzs 12V US (0+ ) = U V R R R 12 6 6 6 6 S 2 4 4 = + = + U V R R R R R 12 3 2 6 2 // // S 3 4 2 3 4 = + = + uzs(∞)= iLzs(∞) = uzs(∞)/ R3=3/3 =1(A) R0= (Ω) 3 3 3 6 2 4 2 4 + = + = + R R R R R τ= L/R0= 0.5s iLzs (t) =1 - e -2t (A) , uzs(t) = 3 + 3e-2t (V) ,t≥0 1. 独立初始值置零!0+时刻 电感相当于开路,若是电容呢? 2. 计算初始值、稳态值、时常数 3. 代入三要素公式!
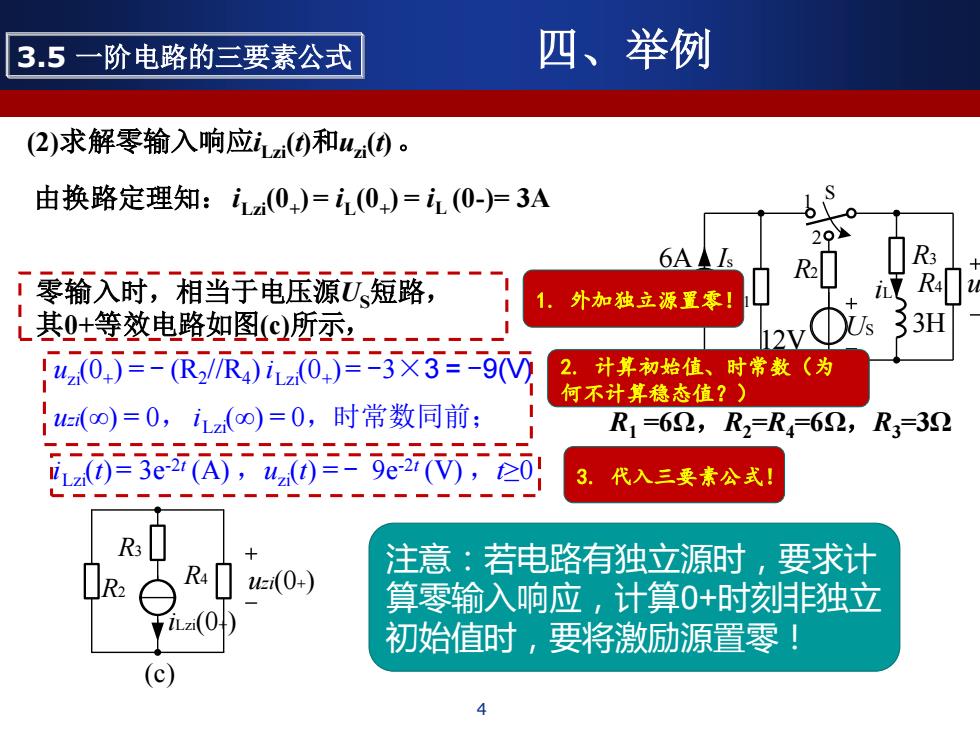
3.5一阶电路的三要素公式 四、举例 (2)求解零输入响应i(④和u(④。 由换路定理知:i(0)=i(0)=i(0-=3A 0 29 6A. R3 零输入时,相当于电压源短路,一 外加独立源置零! R4 L其+等效电路如图(d所示 12V Us 33H u0,j三=R/R)i0j==33三-90 2.计算初始值、时常数(为 何不计算稳态值?) {(o)=0,i(o)=0,时常数同前: R1=62,R2=R4=62,R3=32 无王荷两! 3.代入三要素公式! R 注意:若电路有独立源时,要求计 ei(0+) 算零输入响应,计算0+时刻非独立 Lzi 初始值时,要将激励源置零! (c)
4 3.5 一阶电路的三要素公式 四、举例 R2 R3 iLzi(0+) (c) R uzi(0+) 4 (2)求解零输入响应iLzi(t)和uzi(t) 。 由换路定理知:iLzi(0+ ) = iL (0+ ) = iL (0-)= 3A uzi(0+ ) = - (R2 //R4 ) iLzi(0+ ) = -3×3 = -9(V) uzi(∞) = 0, iLzi(∞) = 0,时常数同前; iLzi(t) = 3e-2t (A) ,uzi(t) = - 9e-2t (V) ,t≥0 R2 6A Is US 12V 3H iL u S 1 2 (a) R1 R4 R3 R1 =6Ω,R2 =R4=6Ω,R3=3Ω 零输入时,相当于电压源US短路, 其0+等效电路如图(c)所示, 注意:若电路有独立源时,要求计 算零输入响应,计算0+时刻非独立 初始值时,要将激励源置零! 1. 外加独立源置零! 2. 计算初始值、时常数(为 何不计算稳态值?) 3. 代入三要素公式!
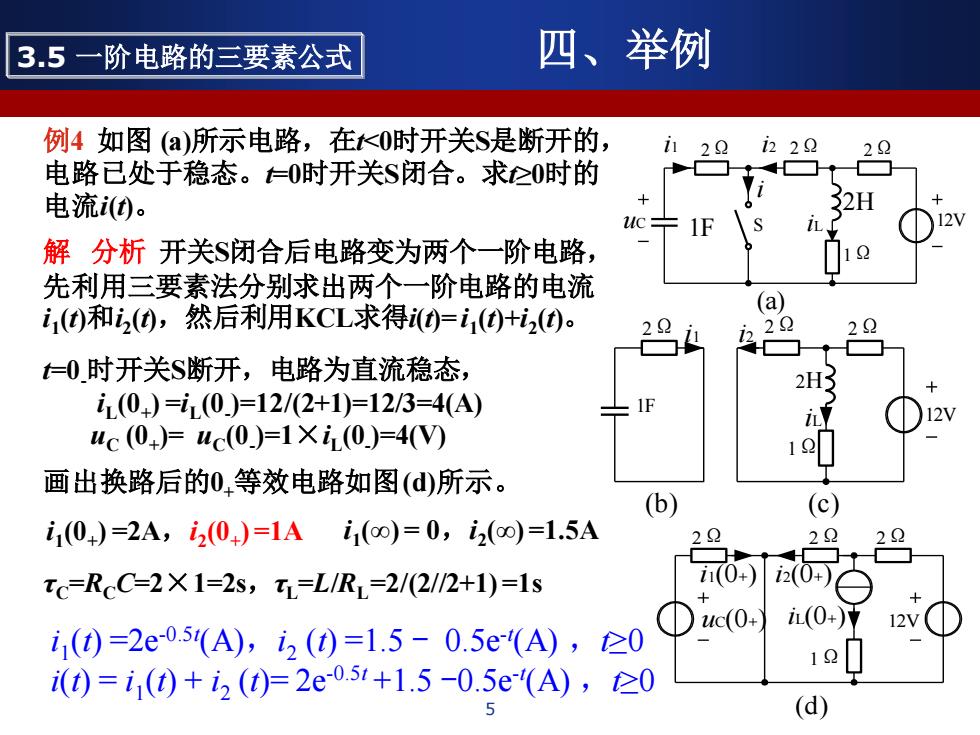
3.5一阶电路的三要素公式 四、举例 例4如图(a)所示电路,在K0时开关S是断开的, 1122 i222 22 电路已处于稳态。仁0时开关$闭合。求≥0时的 电流(④。 WC- 1 解分析开关$闭合后电路变为两个一阶电路, 先利用三要素法分别求出两个一阶电路的电流 (a) i1)和(),然后利用KCL求得i0=i()+i2(0)。 22 22 =O时开关S断开,电路为直流稳态, 2H3 i(0)=i(0)=12/(2+1)=12/3=4(A) 1F uc(0+)=uc(0.)=1Xi(0)=4V 12 画出换路后的0,等效电路如图(d)所示。 (b) (c) i1(0+)=2A,i20)=1Ai1(oo)=0,i2(oo)=1.5A 22 2 xc=RcC=2X1=2s,t=L/RL=2/2/2+1)=1s 0i0- uc(0) (0+)7 12V i1()=2e0.5(A),i2(0=1.5-0.5e-(A),≥0 12 i(0=i1()+i2()=2e051+1.5-0.5e(A),仑0 5 (d)
5 例4 如图 (a)所示电路,在t<0时开关S是断开的, 电路已处于稳态。t=0时开关S闭合。求t≥0时的 电流i(t)。 (a) S 12V 1Ω 2Ω 2Ω 2Ω 2H i1 i2 i uC 1F iL 解 分析 开关S闭合后电路变为两个一阶电路, 先利用三要素法分别求出两个一阶电路的电流 i 1 (t)和i 2 (t),然后利用KCL求得i(t)=i 1 (t)+i 2 (t)。 2Ω 1F i1 i2 2H iL 1Ω 2Ω 2Ω 12V (b) (c) t=0-时开关S断开,电路为直流稳态, iL (0+ ) =iL (0- )=12/(2+1)=12/3=4(A) uC (0+ )= uC (0- )=1×iL (0- )=4(V) τC =RCC=2×1=2s,τL =L/RL =2/(2//2+1) =1s 画出换路后的0+等效电路如图(d)所示。 2Ω 2Ω 2Ω 1Ω uC(0+) iL(0+) 12V i1(0+) i2(0+) (d) i 1 (0+ ) =2A,i 2 (0+ ) =1A i 1 (∞) = 0,i 2 (∞) =1.5A i 1 (t) =2e-0.5t (A),i 2 (t) =1.5 - 0.5e-t (A) ,t≥0 i(t) = i 1 (t) + i 2 (t)= 2e-0.5t +1.5 -0.5e-t (A) ,t≥0 3.5 一阶电路的三要素公式 四、举例

3.5一阶电路的三要素公式 四、举例 例5如图(a)所示电路,在t0 回到原电路计算电流()。 10V 0.1F 2i(t)+uc(t)12 V 12-4e@=1+7.5e0(④,t>06 2
6 例5 如图 (a)所示电路,在t < 0时开关S位于b点,电路已处于稳态。t = 0 时开关S由b点切换至a点。求t≥0时的电压uC(t)和电流i(t)。 a S b 0.1F 12V 5V i 4i uC 2Ω 6Ω 2.5Ω 思路:戴维南等效后得右下等效电路,先解决uC(t),因为戴维南会搞丢i a S b 0.1F 5V 10V uC 1Ω 2.5Ω 初始值:uC (0+ ) = uC (0- ) = -5V 稳态值:uC(∞) = 10V 时常数:τC =R0C=1×0.1=0.1s 利用三要素公式,得 回到原电路计算电流i(t) 。 ( ) 10 ( 5 10) 10 15 ( ), 0 10 10 = + − − = − − − u t e e V t t t C 2i(t) + uC(t) = 12 V 1 7.5 ( ), 0 2 12 ( ) ( ) 10 = + − = − e A t u t i t C t 3.5 一阶电路的三要素公式 四、举例

3.6阶跃函数和阶跃响应 、 单位阶跃函数 一、单位阶跃函数 ▲() 单位阶跃函数在t=0处发生单位跃变,波形 如图(a)。用ε()表示,其定义为: def 1 ,t>0 (a) 0 ,tto &(t-to)= 0,t<to to (d)
7 一、单位阶跃函数 单位阶跃函数在t = 0处发生单位跃变,波形 如图(a)。用ε(t)表示,其定义为: = 0 , 0 1 , 0 ( ) def t t t 0 t 1 ε (t) (a) 阶跃函数的应用之一是描述某些情 况下的开关动作。如图(b)所示的开关 动作,表示在t = 0时把电路接入1V直流 源,电路可简画为图(c)。 (b) (c) ε (t)V u N (t) 1V 1 2 N 若单位直流电源接入的时刻为t0,则可用 延迟单位阶跃函数表示,其波形如图(d)。 0 t 1 (d) t0 ε (t-t0) − = 0 0 def 0 0 , 1 , ( ) t t t t t t 3.6 阶跃函数和阶跃响应 一、单位阶跃函数
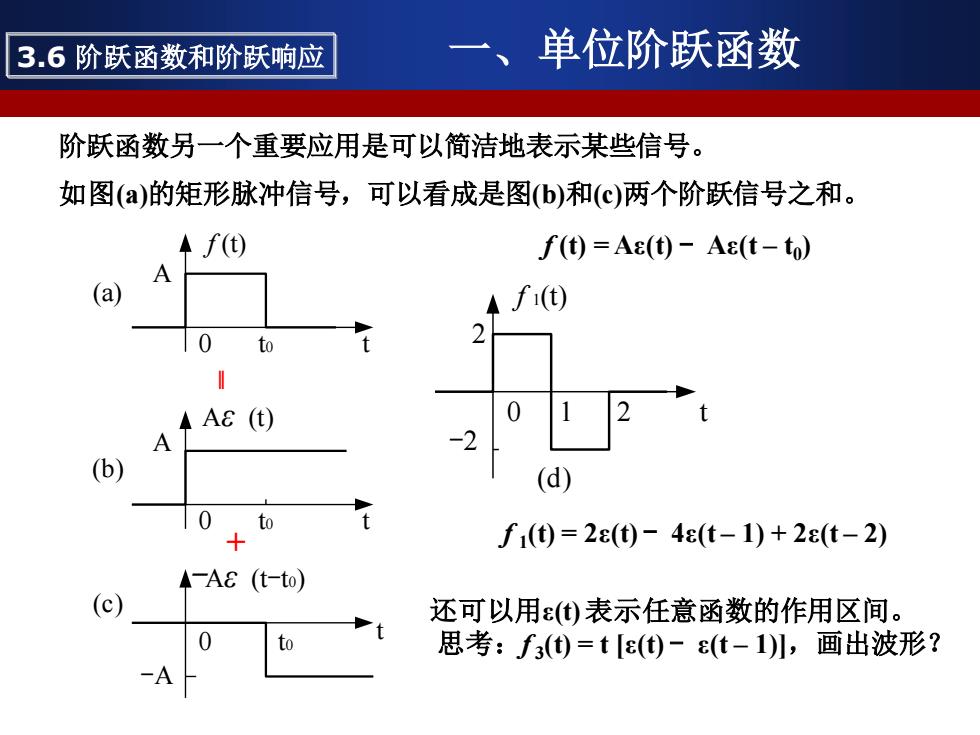
3.6阶跃函数和阶跃响应 、 单位阶跃函数 阶跃函数另一个重要应用是可以简洁地表示某些信号。 如图(a)的矩形脉冲信号,可以看成是图b)和(c)两个阶跃信号之和。 f(t) f()=Aε()-Aε(t-t) (a) fi(t 2 ◆AE(t) 0 -2 (d) to f1(t)=2()-4ε(t-1)+2ε(t-2) ◆一Ae(t-to) 还可以用ε①)表示任意函数的作用区间。 0 to 思考:f3()=t[ε()-ε(t-1)儿,画出波形?
阶跃函数另一个重要应用是可以简洁地表示某些信号。 如图(a)的矩形脉冲信号,可以看成是图(b)和(c)两个阶跃信号之和。 0 t A (b) t0 Aε (t) 0 t A (a) t0 f (t) t 0 -Aε (t-t0) -A t0 (c) ‖ + f (t) = Aε(t) - Aε(t – t0 ) 0 t (d) 1 f 1(t) 2 2 -2 f 1 (t) = 2ε(t) - 4ε(t – 1) + 2ε(t – 2) 还可以用ε(t) 表示任意函数的作用区间。 思考:f 3 (t) = t [ε(t) - ε(t – 1)],画出波形? 3.6 阶跃函数和阶跃响应 一、单位阶跃函数

3.6阶跃函数和阶跃响应 二、阶跃响应 二、阶跃响应 1、定义:当激励为单位阶跃函数ε(0)时,电路的零状态响应称为单位 阶跃响应,简称阶跃响应,用g()表示。一阶电路的阶跃响应仍可用 三要素法求得。 2、线性时不变电路的性质: 4f() Ayr(t) (1)零状态响应与外加激励之间满 A 足齐次性和叠加性(称零状态线性)。 即,若f()→y(),()→y2(), 则af(①+bf()→aym()+by() 激动 零状态响应 线性时不变电路 (2)满足时不变性: 若f()→yr(), ◆f(t-to) ◆Jyr(t-to) 则f(t-to)→yr(t-t) B 0 toto+t O to to+ 9
9 二、阶跃响应 1、定义:当激励为单位阶跃函数ε(t)时,电路的零状态响应称为单位 阶跃响应,简称阶跃响应,用g(t)表示。一阶电路的阶跃响应仍可用 三要素法求得。 2、线性时不变电路的性质: (1)零状态响应与外加激励之间满 足齐次性和叠加性(称零状态线性)。 即,若f1 (t)→ yf1(t), f2 (t)→ yf2(t) , 则 a f1 (t) + b f2 (t) → a yf1(t) + byf2(t) (2)满足时不变性: 若f(t)→ yf (t), 则f(t - t0 )→ yf (t - t0 ) 0 t A f (t) τ t yf (t) B 0 τ 0 t A f (t-t0) t0+ τ t yf (t-t0) B t0 0 t0 t0+ τ 线性时不变电路 激励 零状态响应 3.6 阶跃函数和阶跃响应 二、阶跃响应

3.6阶跃函数和阶跃响应 三、举例 三、举例 例如图(a)所示电路,(1)以uc)为输出,求 电路的阶跃响应g():(2)若激励的波形如 图b),求电路的零状态响应uc()。 is(t) uc(t) 解(1)用三要素法。根据阶跃响应g(①)的定义, 0.2F 知uc(0+)=0;激励is=ε()A,可得 uc(co)=6X1=6V (a) =RC=(6+4)×0.2=2s 故g0)=6(1-et2)ε(0 Ais(t)/A (2)is=2ε()-2ε(t-2)A,根据线性时不变性 质,得零状态响应 2 t/s uc()=2g)-2gt-2) =12(1-et2)ε()-121-et-221εt-2)V (b) 10
10 三、举例 例 如图 (a)所示电路,(1)以uC(t)为输出,求 电路的阶跃响应g(t);(2)若激励iS的波形如 图(b),求电路的零状态响应uC(t)。 解 (1)用三要素法。根据阶跃响应g(t)的定义, 知uC(0+ ) = 0 ;激励iS =ε(t) A,可得 uC(∞) = 6×1 = 6V τ=RC = (6+4) ×0.2 =2s 故 g(t) = 6(1 – e -t/2) ε(t) (2) iS = 2 ε(t) - 2 ε(t -2) A ,根据线性时不变性 质,得零状态响应 uC(t) = 2 g(t) - 2 g(t -2) = 12(1 – e -t/2) ε(t) – 12[1 – e -(t-2)/2] ε(t-2) V iS(t) uC(t) 0.2F 6Ω 4Ω (a) 0 t/s 2 2 iS(t)/A (b) 3.6 阶跃函数和阶跃响应 三、举例