
知识点回顾 1.何谓动态电路? 描述电路的方程为微分方程,则该电路为动态电路。 动态电路阶数=微分方程阶数 2.如何求解动态电路方程? 经典方法:常微分方程求解,完全解=齐次解+特解y1)=y,()+y,() 一阶直流激励动态电路 齐次解 yh(t)=Ke 时常数 t=RC或L/R (形式与激励无关) 特解A 代入原方程求解 特解 yp(t)=A 待定系数K代入初始值求解 (形式与激励相同)
齐次解 (形式与激励无关) ( ) t hy t Ke t - = 特 解 (形式与激励相同) y t p( ) = A 知识点回顾 1 1. 何谓动态电路? 描述电路的方程为微分方程,则该电路为动态电路。 动态电路阶数=微分方程阶数 2. 如何求解动态电路方程? 经典方法:常微分方程求解,完全解=齐次解+特解 ( ) ( ) ( ) h p y t y t y t = + 一阶直流激励动态电路 时常数 t = RC L R 或 / 特解A 代入原方程求解 待定系数K 代入初始值求解

知识点回顾 ☆举例如图RC电路,Us为直流电压源,当t=0时开关闭合,电容的初 始电压uc(O)=Uo,求20时的uc(①。 解(1)建立电路方程。前面已得 1 dt RC RC串联电路 (2)求齐次解uCh()。特征方程为s±1/RC)三Q 其特征根s=-1/(RC),故, iuch K es K e RC! 1.写出负指数形式齐次解, 并确定时常数 (3)求特解。:激励0s为常数,二特解也是常数。 令1=A,将它入上面薇分方程,得月 -1-1 A= &得特解0A=s- RC RC 2.根据特解形式代入原方 程,确定特解取值 (4)求完全解uc()。lc()=uch()+lc(t)=KeRC+U 常数K由初试条件ucO)=U确定:c(0)=K+Us=U0,解得K=U,-Us1 - luc(t)=Uo-Us)e RC+Us ,t 0 最终得完全解 3.根据初始值确定系数K
☆举例如图RC电路,Us为直流电压源,当t = 0时开关闭合,电容的初 始电压uC(0) = U0,求t≥0时的uC(t)。 解(1)建立电路方程。前面已得 (2)求齐次解uCh(t)。特征方程为s + 1/(RC) = 0 其特征根 s = - 1/(RC),故 (3)求特解uCp(t)。∵激励Us为常数,∴特解也是常数。 令 uCp(t) = A,将它代入上面微分方程,得 故得特解 uCp(t) = A = Us (4)求完全解uC (t)。 uC (t) = uCh(t) + uCp(t) = 常数K由初试条件uC (0) = U0确定: uC(0) = K + Us = U0 ,解得 K = U0 - Us C S C U RC u t RC u 1 1 d d + = 1 e e t st R C C h u K K - = = 1 1 A US RC RC = 1 e t R C K US - + 1 0 ( ) ( ) e , 0 t R C C S S u t U U U t - = - + ? S US uR uC R C i RC串联电路 知识点回顾 1. 写出负指数形式齐次解, 并确定时常数 2. 根据特解形式代入原方 程,确定特解取值 最终得完全解! 3. 根据初始值确定系数K

知识点回顾 3.为何要确定初始值,初始值分类? 为了确定齐次解的待定系数K ·独立初始值:4C,2,特征:不能跃变 。 非独立初始值:除,外的电压/电流,特征:可能跃变 4.如何求初始值(@0+时刻)? ·独立初始值:换路定律一c(0,)=c(0.),(0,)=i(0.) 其中“(0),(0)可通过分析换路前响应得到(电容开路、电感短路) ·非独立初始值:(1)使用换路定律确定独立初始值,(2)将独立初始 值使用对应独立源替代,(3)再通过电阻电路分析可得非独立初始值 无 无 us(t uc(t) s(0- )hc(0) 电 阻 is(t) iu(t) is(0+) 电 电 路 i(0-)7 (a)t)>0时的原电路 (b)0+等效电阻电路
知识点回顾 3 3. 为何要确定初始值,初始值分类? 4. 如何求初始值(@0+时刻)? 为了确定齐次解的待定系数K! • 独立初始值: ,特征:不能跃变 • 非独立初始值:除 外的电压/电流,特征:可能跃变 , C L u i , C L u i • 独立初始值:换路定律—— 其中 可通过分析换路前响应得到(电容开路、电感短路) • 非独立初始值:(1)使用换路定律确定独立初始值,(2)将独立初始 值使用对应独立源替代,(3)再通过电阻电路分析可得非独立初始值 (0 ) (0 ), (0 ) (0 ) C C L L u u i i + - + - = = (0 ), (0 ) C L u i - - 无 源 电 阻 电 路 uS(t) iS(t) uC(t) iL(t) C L (a) t>0 时的原电路 无 源 电 阻 电 路 uS(0+) iS(0+) uC(0+) iL(0+) (b) 0+等效电阻电路
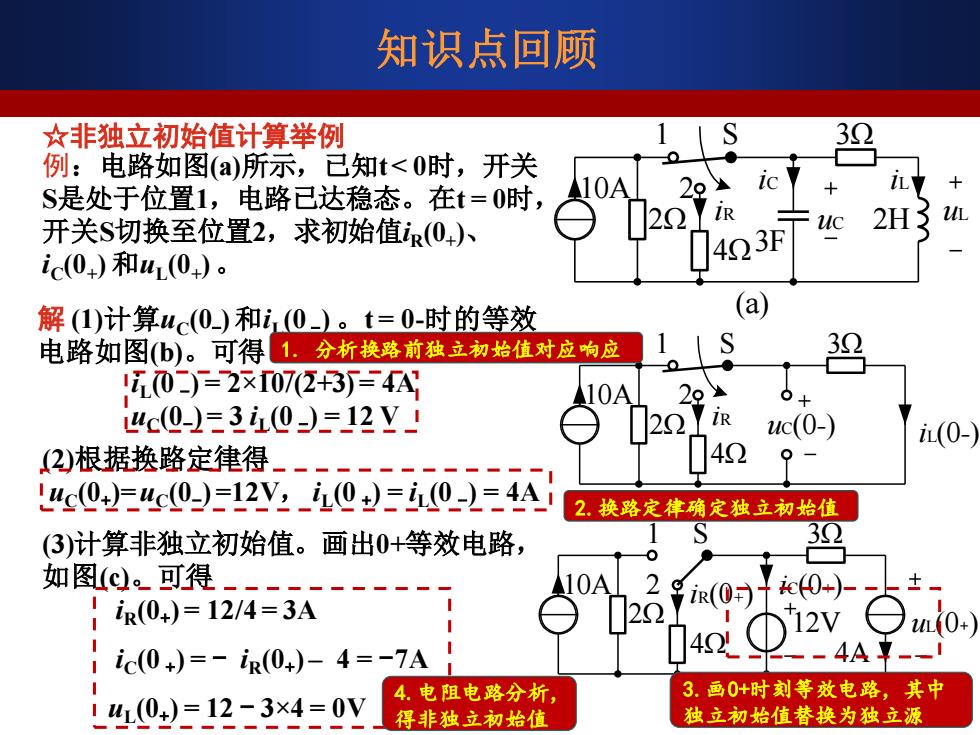
知识点回顾 ☆非独立初始值计算举例 3 例:电路如图(a)所示,已知t<0时,开关 10A 29 i7 S是处于位置1,电路已达稳态。在t=0时, 开关S切换至位置2,求初始值(04)、 22R uc 2H3 uL ic(0+)和u(0)。 423F 解(1)计算u(0)和i(0)。t=0-时的等效 (a) 电路如图b)。可得1.分析换路前独立初始值对应响应 S 32 0二)=2x0723=4A 10 29 uc0-=3i0)=12Y」 22 uc(0-) i(0- (2)根据换路定律得_ 4Ω uc(0)-uc(0)=12V:iL(0)=in(0-)-4Ai 2.换路定律确定独立初始值 (3)计算非独立初始值。画出0+等效电路, 32 如图0。可得- R(0+)=12/4=3A R(0十0+) iic(0+)=-iR0+)-4=-7A 74 -4A L40)=12二3x4=0Y 4.电阻电路分析, 3.画0+时刻等效电路,其中 得非独立初始值 独立初始值替换为独立源
4 ☆非独立初始值计算举例 例:电路如图(a)所示,已知t < 0时,开关 S是处于位置1,电路已达稳态。在t = 0时, 开关S切换至位置2,求初始值iR(0+ )、 iC(0+ ) 和uL(0+ ) 。 1 S 2 3F 2H 3Ω 2Ω 4Ω 10A iR iC uC iL uL (a) 解 (1)计算uC(0- ) 和iL(0 - ) 。t = 0-时的等效 电路如图(b)。可得 iL(0-) 1 S 2 3Ω 2Ω 4Ω 10A iR (b) uC(0-) iL (0 - ) = 2×10/(2+3) = 4A uC(0- ) = 3 iL(0 - ) = 12 V (2)根据换路定律得 uC(0+ )= uC(0- ) =12V, iL (0 + ) = iL (0 - ) = 4A (3)计算非独立初始值。画出0+等效电路, 如图(c)。可得 uL(0+) iC(0+) 1 S 2 3Ω 2Ω 4Ω 10A (c) 12V 4A iR(0+) iR(0+ ) = 12/4 = 3A iC(0 + ) = - iR(0+ ) – 4 = -7A uL(0+ ) = 12 - 3×4 = 0V 知识点回顾 1. 分析换路前独立初始值对应响应 2.换路定律确定独立初始值 3.画0+时刻等效电路,其中 独立初始值替换为独立源 4.电阻电路分析, 得非独立初始值

知识点回顾 5.至此,我们得到了什么? 1.时常数 2.特解 t=RC或LIR 齐次解 h)=Kef。 特解 代入方程确定 Yp(t)=A (形式与激励无关) (形式与激励相同) 3.初始值 y(0+) 6.特殊情形的响应 动态电路响应可视为初始储能(独立初始值)与独立源共同激励的 结果,因此,存在如下两种特殊情形的响应: ·无独立源激励,仅由初始储能激励一零输入响应y),与初始 状态间满足齐次性,即零输入线性;零输入响应特解=0(wy?), 仅需(1)确定时常数,(2)并根据初始值确定待定系数K即可 ·无初始储能激励,仅由独立源激励—零状态响应'云),即 4e(0,)=0z(0)=0时的响应(注意:不是y(0+)=0)
知识点回顾 5 5. 至此,我们得到了什么? 6. 特殊情形的响应 齐次解 (形式与激励无关) ( ) t hy t Ke t - = 特 解 (形式与激励相同) y t A p( ) = 3.初始值 1.时常数 2.特解 t = RC L R 或 / 代入方程确定 y(0 ) + 动态电路响应可视为初始储能(独立初始值)与独立源共同激励的 结果,因此,存在如下两种特殊情形的响应: • 无独立源激励,仅由初始储能激励——零输入响应 ,与初始 状态间满足齐次性,即零输入线性;零输入响应特解=0(why?), 仅需(1)确定时常数,(2)并根据初始值确定待定系数K即可 • 无初始储能激励,仅由独立源激励——零状态响应 ,即 时的响应(注意:不是y(0+)=0) zi y t( ) zs y t( ) (0 ) 0, (0 ) 0 C L u i + + = =

3.4一阶动态电路的响应 二、零状态响应 二、零状态响应 定义:当电路的初始储能为零(即初始状态 为零)时,仅由外加激励所引起的响应,称 R 为零状态响应,记为y()。 例:电路如图(a)所示,已知t<0时,开关S是闭合,电路已达稳态。在t= 0时,开关S断开,求≥0时,电容电压uc()(注意:该响应为零状态响应, 为何?)。 解:所求响应为零状态响应。≥0时,根据KCL有i心+=s 由于ic=C duc/dt,iR=ucR,代入上式得 duc 1 1 +-uc 式中=RC,初始值uc(0)=0 dtπ uc(t)uch(t)ucp(t) 对应的齐次解为uc,(t)=Ket 6
6 二、零状态响应 定义:当电路的初始储能为零(即初始状态 为零)时,仅由外加激励所引起的响应,称 为零状态响应,记为yzs(t)。 例:电路如图(a)所示,已知t < 0时,开关S是闭合,电路已达稳态。在t = 0时,开关S断开,求t≥0时,电容电压uC(t) (注意:该响应为零状态响应, 为何?)。 解: 所求响应为零状态响应。t≥0时,根据KCL有 iC + iR = Is 由于 iC= C duC/dt, iR = uC/R,代入上式得 C S C I C u t u 1 1 d d + = 式中τ=RC,初始值uC(0+ ) = 0 uC(t) = uCh(t) + uCp(t) 对应的齐次解为 t uCh t K − ( ) = e S uC IS iC iR C R 3.4 一阶动态电路的响应 二、零状态响应
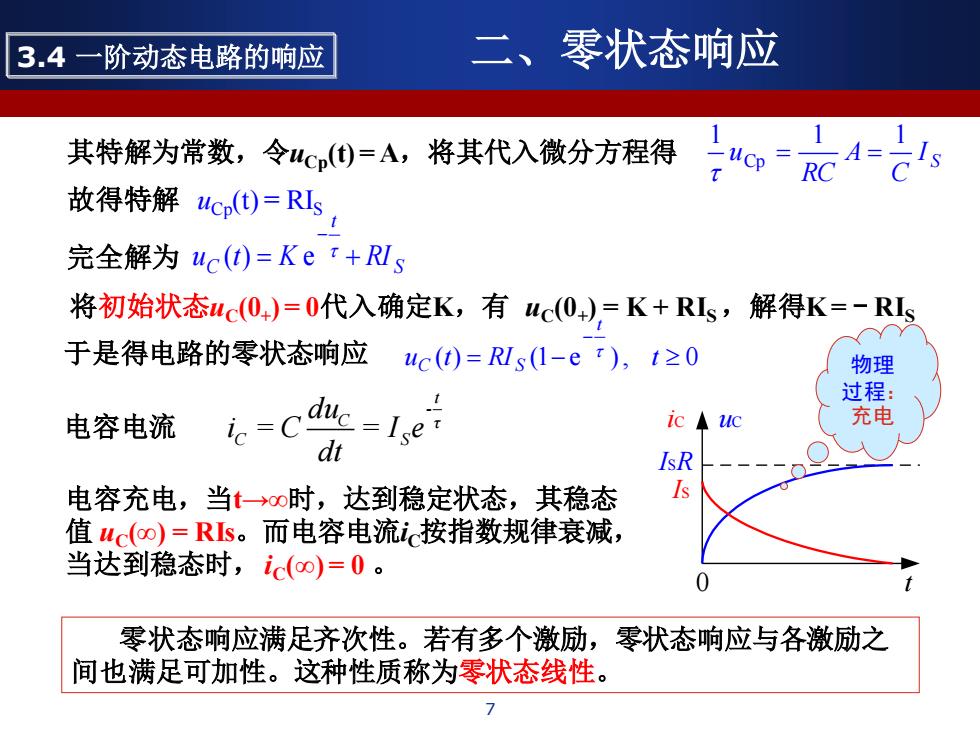
3.4一阶动态电路的响应 二、零状态响应 其特解为常数,令uCp)=A,将其代入微分方程得 故得特解uc(①)=RIs 完全解为uc(t)=Ket+RIs 将初始状态uc04)=0代入确定K,有uc(0),=K+Rs,解得K=-RIs 于是得电路的零状态响应uc)=Rs(I-eT),t≥0 物理 过程: 电容电流 ie-Cduc -lye ic◆uc 充电 dt IsR 电容充电,当t→时,达到稳定状态,其稳态 值uc(o)=Rs。而电容电流i按指数规律衰减, 当达到稳态时,ic(o)=0。 零状态响应满足齐次性。若有多个激励,零状态响应与各激励之 间也满足可加性。这种性质称为零状态线性
7 其特解为常数,令uCp(t) = A,将其代入微分方程得 S I C A RC u 1 1 1 Cp = = 故得特解 uCp(t) = RIS 完全解为 S t uC t = K + RI − ( ) e 将初始状态uC(0+ ) = 0代入确定K,有 uC(0+ ) = K + RIS ,解得K = - RIS 于是得电路的零状态响应 ( ) = (1− e ), 0 − u t RI t t C S iC uC ISR IS 0 t 电容电流 t - C τ C S du i = C = I e dt 电容充电,当t→∞时,达到稳定状态,其稳态 值 uC(∞) = RIs。而电容电流iC按指数规律衰减, 当达到稳态时,iC(∞) = 0 。 零状态响应满足齐次性。若有多个激励,零状态响应与各激励之 间也满足可加性。这种性质称为零状态线性。 物理 过程: 充电 3.4 一阶动态电路的响应 二、零状态响应

3.4一阶动态电路的响应 三、全响应 三、全响应 定义:电路在外加激励和初始状态共同作用下所产生的响 应,称为全响应。 根据叠加定理,全响应又可以分解为 全响应=零输入响应+零状态响应,即y)=y)+y() 对于初始状态不为零,外加激励也不为零的电路。 。 初始状态单独作用时(独立源置0)时产生的响应 就是零输入响应分量; 而外加激励单独作用时[即令uc(0+)=0或(0+)=0]时 求得的响应就是零状态响应分量
8 三、全响应 定义:电路在外加激励和初始状态共同作用下所产生的响 应,称为全响应。 根据叠加定理,全响应又可以分解为 全响应 = 零输入响应+ 零状态响应,即 y(t) = yzi(t) + yzs(t) 对于初始状态不为零,外加激励也不为零的电路。 • 初始状态单独作用时(独立源置0)时产生的响应 就是零输入响应分量; • 而外加激励单独作用时[即令uC(0+ ) = 0或iL (0+ )=0]时 求得的响应就是零状态响应分量。 3.4 一阶动态电路的响应 三、全响应
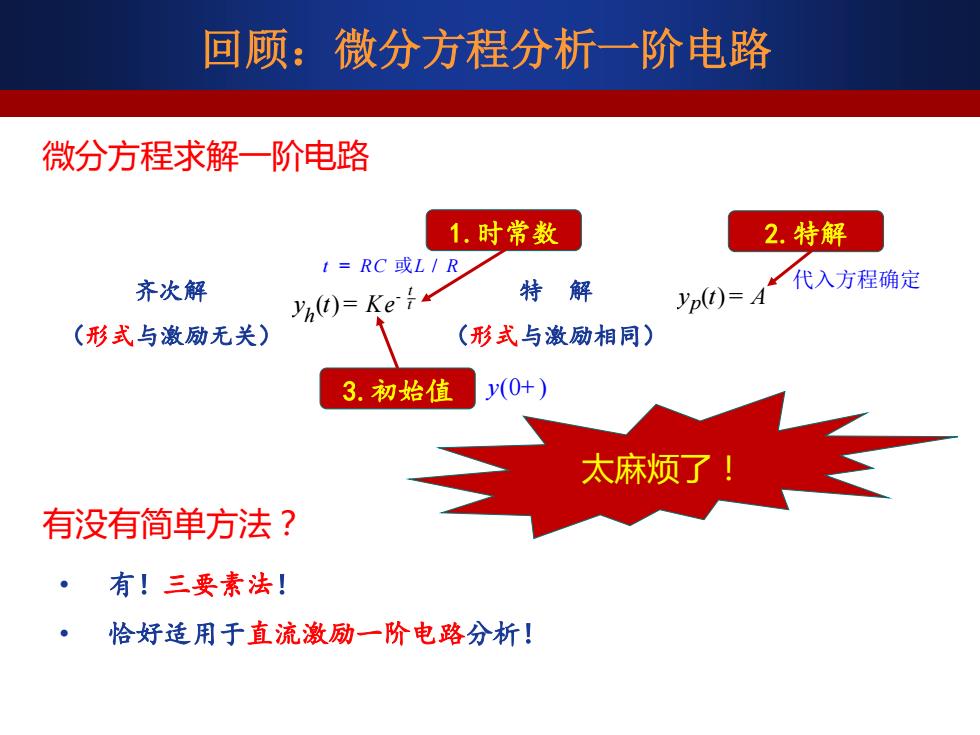
回顾:微分方程分析一阶电路 微分方程求解一阶电路 1.时常数 2.特解 t=RC或L/R 齐次解 特解 Yp(t)=A 代入方程确定 yh(t)=Ke (形式与激励无关) (形式与激励相同) 3.初始值 y(0+) 太麻烦了! 有没有简单方法? ·有!三要素法! 恰好造用于直流激励一阶电路分析!
回顾:微分方程分析一阶电路 微分方程求解一阶电路 齐次解 (形式与激励无关) ( ) t hy t Ke t - = 特 解 (形式与激励相同) y t A p( ) = 3.初始值 1.时常数 2.特解 t = RC L R 或 / 代入方程确定 y(0 ) + 太麻烦了! 有没有简单方法? • 有!三要素法! • 恰好适用于直流激励一阶电路分析!

3.5一阶电路的三要素公式 一、三要素公式的推出 一阶电路只含一个动态元件,因此,换路后可利用戴维南定理,将任何 一阶电路简化为如图(a)b)两种形式之一。 电容电压uc()和电感电流()为响应 duc I di+RCc =RCus IL=-us dt L L (a) (b) y()表示响应uc或,f)表示外加激励s,上述方程可统一表示如下: dy④+0)=bf dt 微分方程的解为:yt)=M24码+y,(t) Yh(t)
一、三要素公式的推出 一阶电路只含一个动态元件,因此,换路后可利用戴维南定理,将任何 一阶电路简化为如图(a)(b)两种形式之一。 (a) (b) C uS uC R R uS L iL 电容电压uC(t)和电感电流iL (t)为响应 C S C u RC u t RC u 1 1 d d + = L S L u L i L R t i 1 d d + = y(t)表示响应uC或iL,f (t)表示外加激励uS,上述方程可统一表示如下: d ( ) 1 ( ) ( ) d y t y t bf t t t + = 3.5 一阶电路的三要素公式 / ( ) ( ) ( ) h t p y t y t e K y t - t 微分方程的解为: = + 1442 443