
历粤毛子代技大 XIDIAN UNIVERSITY Hood -19dOT mo I.动态电路模块 第4章正弦稳态分析
XiDian II.动态电路模块 第4章 正弦稳态分析

目录 必4.1正弦量 4.2相量法的基本概念 4.3电路定律的相量形式 4.4阻抗与导纳 冬4.5正弦稳态电路的功率 4.6互感耦合电路 04.7 变压器 第4章作业:4-64-84-94-134-164-224-254-28. 4-304-354-404-434-454-49
目录 ❖4.1 正弦量 ❖4.2 相量法的基本概念 ❖4.3 电路定律的相量形式 ❖4.4 阻抗与导纳 ❖4.5 正弦稳态电路的功率 ❖4.6 互感耦合电路 ❖4.7 变压器

4.1正弦量 、三要素 按正孩(余孩)规律变化的电压、电流称为正孩电压、电流,统称为正弦量 (正弦波或正弦交流电)。 瞬时值表达式:i(t)=Icos(ot+p:),(t)=Ucos(ot+p) Um(Im):正弦量的最大值,称为振幅: i◆W 2元 Um ot+0:正弦量的瞬时相位角,简称相 位,弧度(rad或度(o)。 当t=0时的相位Φ称初相位,简称初相: 通常在-≤p≤π主值内取值。 @是正弦量相位变化的速率,称为角频 率,单位:rad/s。 9>0 振幅、初相、角频率称为正弦量的三要素:三要素可唯一确定正弦量
按正弦(余弦)规律变化的电压、电流称为正弦电压、电流,统称为正弦量 (正弦波或正弦交流电)。 瞬时值表达式:i(t)=Imcos(ωt + i ) , u(t)=Umcos(ω t + u ) Um( Im):正弦量的最大值,称为振幅; ωt + :正弦量的瞬时相位角,简称相 位,弧度(rad)或度( o )。 当t = 0 时的相位 称初相位,简称初相; 通常在-π≤ ≤π主值内取值。 ω是正弦量相位变化的速率,称为角频 率,单位:rad/s。 振幅、初相、角频率称为正弦量的三要素:三要素可唯一确定正弦量。 ω t i u u i Um Im 0 2π 0 u 0 i 4.1 正弦量 一、 三要素
4.1正弦量 三要素 说明(I)角频率(angular frequency).ω反映正孩量变化快慢。 (2)初相位(initial phase angle)p:反映了正孩量的计时起点。 同一个正弦量,计时起点不同,初相位不同。 一般规定:|0π。 0=00=元/20=-元/2 角频率ω、频率f和周期T之间的关系:o= 2π=2元f
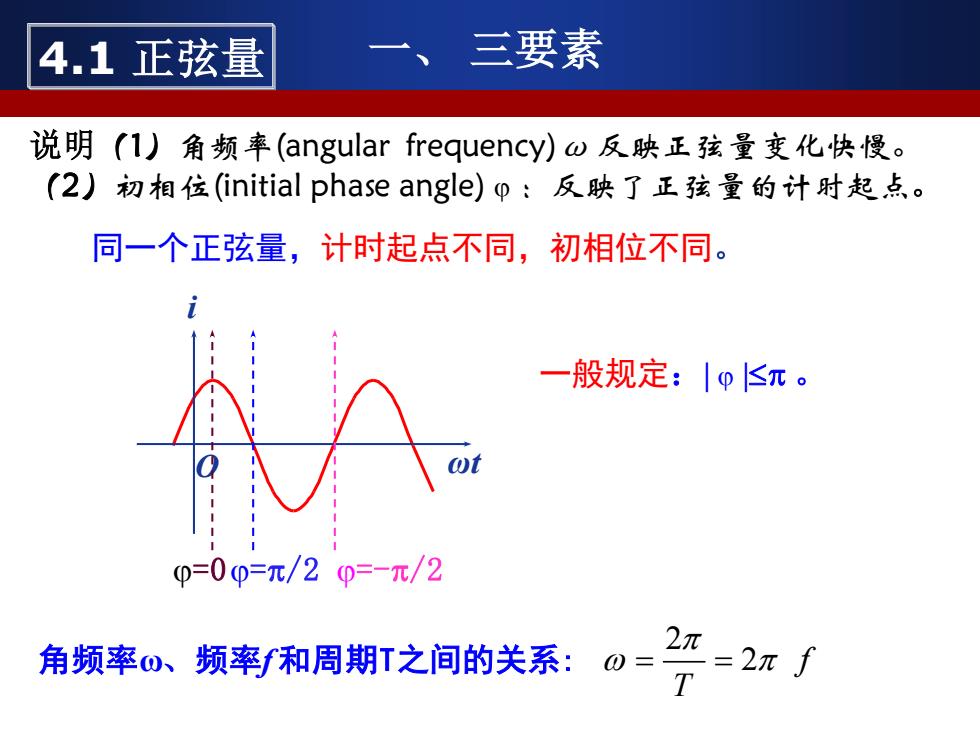
说明(1)角频率(angular frequency)ω 反映正弦量变化快慢。 (2)初相位(initial phase angle) :反映了正弦量的计时起点。 同一个正弦量,计时起点不同,初相位不同。 ωt i O =0=/2 =-/2 一般规定:| | 。 4.1 正弦量 一、 三要素 角频率ω、频率f 和周期T之间的关系: f T 2 2 = =

4.1正弦量 二、相位差 两个同频率的正弦波之间的相位之差称为相位差。记为0。 例如,设有相同频率的电压和电流 u(t)=Umcos(@t+u),i(t)=Imcos(ot+i) 0=(0t+0u)-(ot+0i)=04p;相 位差即为初相之差。 日仍在-≤日≤π主值范围内取值。 ●若0=04-p>0,称电压(t)超前电流 i(t)0角,或(t)落后u(①0角。(u比i先到达 最大值) ●若0=0m-p,<0,称电压(t)落后电流 i(t)川0|角,或(t)超前后d(0川0角
两个同频率的正弦波之间的相位之差称为相位差。记为θ。 t u, i u i u i θ 0 4.1 正弦量 二、 相位差 例如,设有相同频率的电压和电流 u(t)=Umcos(ω t + u ) ,i(t) =Imcos(ωt + i ) θ= (ω t + u ) - (ωt + i ) = u - i 相 位差即为初相之差。 θ仍在-π≤ θ ≤π主值范围内取值。 •若θ= u - i > 0,称电压u(t)超前电流 i(t) θ角,或i(t)落后u(t)θ角。(u 比 i 先到达 最大值); •若θ= u - i < 0,称电压u(t)落后电流 i(t) |θ|角,或i(t)超前后u(t)|θ|角

4.1正弦量 二、相位差 几种特殊相位关系: ●若0=04-0:=0, 称电压()与电流()同相。 ●若0=0u-p=±元, 称电压(0)与电流)反相。 ●若0=pu-0=士π/2, 称电压(0)与电流()正交。 u,i 注意:0=π/2:u超前iπ/2,不说u 落后i3π/2;i落后uπ/2,不说i超 前u3π/2。主值范围|0≤π
4.1 正弦量 二、 相位差 几种特殊相位关系: • 若θ= u - i = ±π, 称电压u(t)与电流i(t) 反相。 t u, i u i O • 若θ= u - i = 0, 称电压u(t)与电流i(t) 同相。 • 若θ= u - i = ±π/2, 称电压u(t)与电流i(t) 正交。 t u, i u O i t u, i u i O 注意:θ= /2:u 超前 i /2, 不说 u 落后 i 3/2; i 落后 u /2, 不说 i 超 前u 3/2。主值范围|θ|
4.1正弦量 三、有效值 周期电压、电流的瞬时值随时间变化,为了简明地衡量其大小,常采 用有效值。 当一交流电和直流电分别通过两个相等的电阻时,若 在交流电的一个周期T内,两个电阻消耗的能量相等,则 称该直流电的数值为交流电的有效值。 1产7=j0Rd, WDc=12R 文流电选0台有效准兰。户0) def def 交流电压u()的有效值
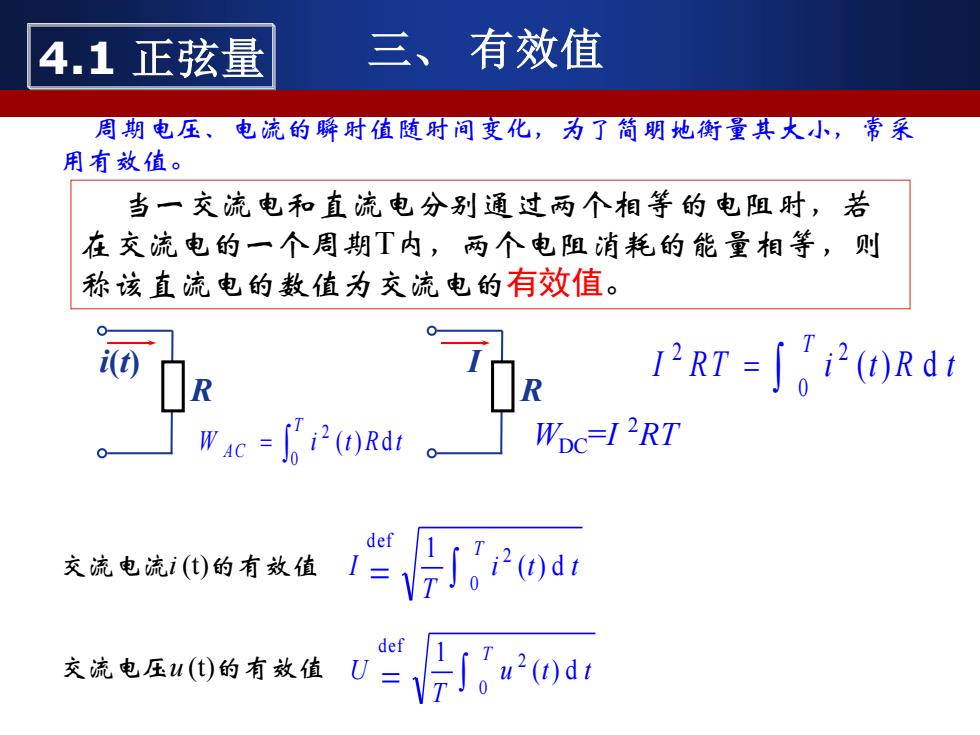
周期电压、电流的瞬时值随时间变化,为了简明地衡量其大小,常采 用有效值。 当一交流电和直流电分别通过两个相等的电阻时,若 在交流电的一个周期T内,两个电阻消耗的能量相等,则 称该直流电的数值为交流电的有效值。 = T I R T i t R t 0 2 2 ( ) d 交流电流i (t)的有效值 = T i t t T I 0 2 def ( ) d 1 交流电压u (t)的有效值 = T u t t T U 0 2 def ( ) d 1 R i(t) = T A C W i t R t 0 2 ( ) d R I WDC =I 2RT 4.1 正弦量 三、 有效值

4.1正弦量 三、有效值 正弦电流(t)的有效值为 记住! 1 、12 cos2(wt+f,)dt I= 1m=0.7071m 2 √2 27T ò(1+cos鼴wt+f,))d 1 U 注意区分瞬时值、 Um=0.707Um 0 2 振幅、有数值的 2 特号:i,lm,I u(t)气J2Ucos(ωt+pu) 2 0.7071m i(t)=√2lcos(ωt+pi) 通常所说的正孩交流电的大小都是指有效值。如民用交 流电压220V。交流仪表所指示的读数、电气设备的额定值等 都是指有效值。但绝缘水平、耐压值指的是振幅
正弦电流 i(t)的有效值为 m m m m U U U I I I 0.707 2 1 0.707 2 1 = = = = 通常所说的正弦交流电的大小都是指有效值。如民用交 流电压220V。交流仪表所指示的读数、电气设备的额定值等 都是指有效值。但绝缘水平、耐压值指的是振幅。 记住! ( ) 2 2 0 2 0 2 0 2 1 cos ( ) 1 cos 2( ) 2 2 2 0.707 2 T m i T m i m T m m m I I t dt T I t dt T I t T I I I w f w f = + = + + 轾臌 = = = = ò ò u(t) = Ucos(ω t + u ) i(t) = Icos(ωt + i ) 2 2 注意区分瞬时值、 振幅、有效值的 符号:i,Im,I 4.1 正弦量 三、 有效值

4.2相量法的基本概念 复数的有关知识复习 虚数单位j=v- Im A 1.复数的表示 b 直角坐标:A=a+jb A 极坐标:A=Ae0=A∠0 a Re (a)复平面表示的复数 (b)简画法 两种表示法之间的关系: Al=Ja2+62 a =Alcose b 0 arctan- b=41sine a
复数的有关知识复习 虚数单位 j = −1 1. 复数的表示 直角坐标:A = a + jb 极坐标:A = |A|ejθ = |A|∠θ Re Im 0 a b |A| θ θ |A| A A 0 +1 (a)复平面表示的复数 (b)简画法 两种表示法之间的关系: = = + a b θ A a b arctan | | 2 2 = = | | sin | | cos b A a A 4.2 相量法的基本概念

4.2相量法的基本概念 ()加减运算—直角坐标 A+B A=a+jb,A2-aztjb2 A-B 则A1±A2=(a1±a2+j(b1±b2) (2)乘除运算—极坐标 Re 若A1=4101,若A2=4I02 B 符合平行四边形法则 则 A142=4ea42e8:=4l42e8+8,)=41lA3lk01+02 4=1401-Ale9=l4e,)=4∠91-02 A21A,lL021421e021A2 |A2|
(1) 加减运算——直角坐标 若 A1=a1+jb1, A2=a2+jb2 则 A1±A2=(a1±a2 )+j(b1±b2 ) Re Im 0 A+B A B 符合平行四边形法则 -B A-B (2) 乘除运算——极坐标 若 A1=|A1 | / 1 ,若A2=|A2 | / 2 1 2 1 2 ( ) 1 2 1 2 1 2 1 2 1 2 = = = + + A A A e A e A A e A A j j j 则 1 2 2 j ( ) 1 2 1 j 2 2 j 1 2 2 1 1 2 1 | | | | e | | | | | | e | | e | | | | 1 2 1 θ θ A A A A A A A θ A θ A A θ θ θ θ = = = − = − 4.2 相量法的基本概念