
2.4 节点法 一、节点法大 1、节点法:以节点电压为电路变量,并对独立节点用KCL列出用节 点电压表达有关支路电流的方程的求解方法。 列写方程个数:n-1 2、节点电压 在电路中任意选择一个节点为参考节点,其余节点与参考节点 之间的电压,称为节点电压或节点电位,各节点电压的极性均以 参考节点为“”极
2.4 节点法 1 2、节点电压 在电路中任意选择一个节点为参考节点,其余节点与参考节点 之间的电压,称为节点电压或节点电位,各节点电压的极性均以 参考节点为“-”极。 1、节点法:以节点电压为电路变量,并对独立节点用KCL列出用节 点电压表达有关支路电流的方程的求解方法。 一、节点法★ 列写方程个数:n - 1
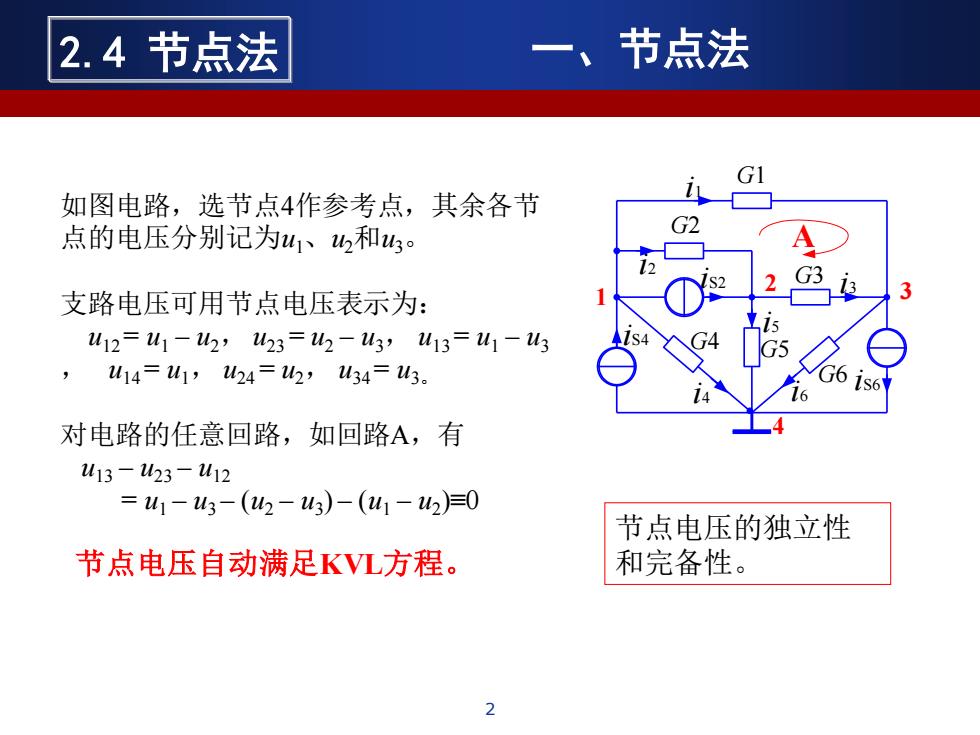
2.4节点法 一、节点法 G1 如图电路,选节点4作参考点,其余各节 点的电压分别记为u1、2和3 G2 G3 支路电压可用节点电压表示为: u12=u1-W2,u23=u2-W3,u13=u1-3 ,u14=u1,u24=u2,u34=3. 对电路的任意回路,如回路A,有 u13-l23-U12 =41-43-(2-43)-(u1-u2)=0 节点电压的独立性 节点电压自动满足KVL方程。 和完备性
2 2.4 节点法 一、节点法 i4 G1 G2 G4 G6 1 i2 iS2 i5 A G3 G5 iS4 iS6 2 3 4 i1 i3 i6 如图电路,选节点4作参考点,其余各节 点的电压分别记为u1、u2和u3。 支路电压可用节点电压表示为: u12 = u1 – u2, u23 = u2 – u3, u13 = u1 – u3 , u14 = u1, u24 = u2, u34 = u3。 对电路的任意回路,如回路A,有 u13 – u23 – u12 = u1 – u3 – (u2 – u3 ) – (u1 – u2 )≡0 节点电压自动满足KVL方程。 节点电压的独立性 和完备性
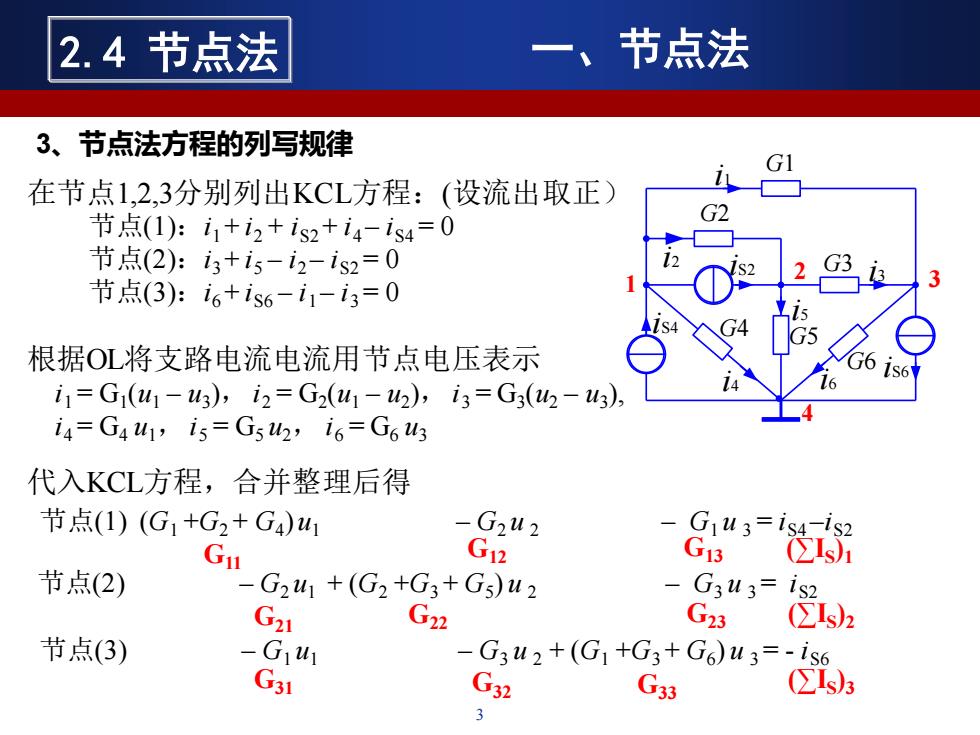
2.4节点法 、节点法 3、节点法方程的列写规律 在节点1,2,3分别列出KCL方程:(设流出取正) 节点(1):i1+i2+is2+i4-is4=0 G2 节点(2):i3+i5-i2-is2=0 节点(3):i6+is6-i1-i3=0 S4 根据OL将支路电流电流用节点电压表示 1S6 i1=G1(w1-w3),i2=G2(u1-w2),i3=G3(2-u3), i4=G4u1,i5=G52,i6=G6w3 代入KCL方程,合并整理后得 节点(1)(G1+G2+G4)u1 -G2u2 - Gu3=is4 1s2 Gn G12 G1 CIs) 节点(2) -G241+(G2+G3+G5)u2 G3u3= G21 G22 G23 s 节点(3) -G1u1 -G3u2+(G1+G3+G6)u3=-is6 G31 G32 G33 CIs): 3
3 i4 G1 G2 G4 G6 1 i2 iS2 i5 G3 G5 iS4 iS6 2 3 4 i1 i3 i6 在节点1,2,3分别列出KCL方程:(设流出取正) 节点(1):i1 + i2 + iS2 + i4 – iS4 = 0 节点(2):i3 + i5 – i2 – iS2 = 0 节点(3):i6 + iS6 – i1 – i3 = 0 根据OL将支路电流电流用节点电压表示 i1 = G1 (u1 – u3 ), i2 = G2 (u1 – u2 ), i3 = G3 (u2 – u3 ), i4 = G4 u1, i5 = G5 u2, i6 = G6 u3 代入KCL方程,合并整理后得 节点(1) (G1 +G2 + G4 )u1 – G2 u 2 – G1 u 3 = iS4 –iS2 节点(2) – G2 u1 + (G2 +G3 + G5 ) u 2 – G3 u 3 = iS2 节点(3) – G1 u1 – G3 u 2 + (G1 +G3 + G6 ) u 3 = - iS6 G11 G22 G33 G12 G13 G21 G23 G31 G32 (∑IS )1 (∑IS )2 (∑IS )3 3、节点法方程的列写规律 2.4 节点法 一、节点法

2.4节点法 、节点法 由电路直接列写节点方程的规律总结 G(i=1,2,3)称为节点的自电导=与节点相连的 所有支路的电导之和,恒取“+”; G称为节点i与节点的互电导=节点与节点之 间共有支路电导之和,恒取“”; (∑s):称为节点的等效电流源=流入节点的所 有电流源电流的代数和。即,电流源电流流 入该节点时取“+,流出时取“-
Gii(i =1,2,3)称为节点i的自电导=与节点i相连的 所有支路的电导之和,恒取“+” ; Gij称为节点i与节点j的互电导=节点i与节点j之 间共有支路电导之和,恒取“-” ; (∑IS )i 称为节点i的等效电流源=流入节点i的所 有电流源电流的代数和。即,电流源电流流 入该节点时取“ + ” ,流出时取“ - ” 。 4 由电路直接列写节点方程的规律总结 2.4 节点法 一、节点法

2.4节点法 一、节点法 4、节点法步骤: (1)指定电路中某一节点为参考点,并标出各独立 节点的电压。 (2)按照规律列出节点电压方程。 (3)联立求解,解出各节点电压。 (4)根据节点电压再求其它待求量
(2)按照规律列出节点电压方程。 (3)联立求解,解出各节点电压。 (4)根据节点电压再求其它待求量。 (1)指定电路中某一节点为参考点,并标出各独立 节点的电压。 4、节点法步骤: 5 2.4 节点法 一、节点法
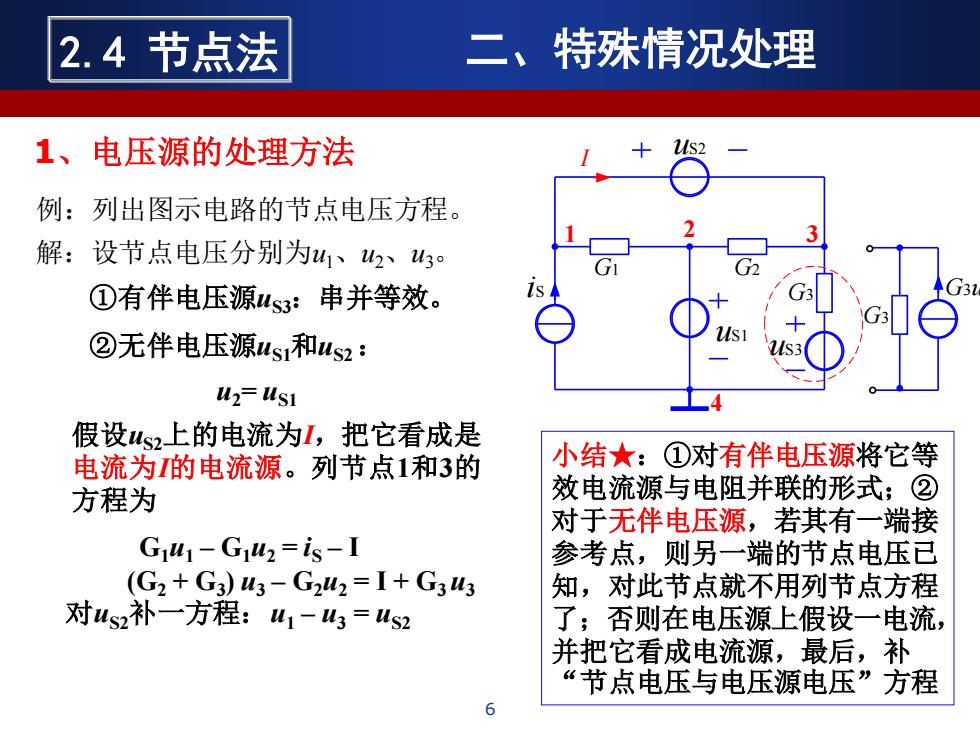
2.4节点法 二、特殊情况处理 1、电压源的处理方法 例:列出图示电路的节点电压方程。 解:设节点电压分别为u1、2、43。 ①有伴电压源us3:串并等效。 ②无伴电压源us1和us2: uz=Usi 假设us2上的电流为I,把它看成是 电流为的电流源。列节点1和3的 小结★:①对有伴电压源将它等 方程为 效电流源与电阻并联的形式;② 对于无伴电压源,若其有一端接 Gi41-Giuz=is-I 参考点,则另一端的节点电压已 (G2+G3)3-G242=I+G33 知,对此节点就不用列节点方程 对Ws2补一方程:u1-山3=us2 了;否则在电压源上假设一电流, 并把它看成电流源,最后,补 “节点电压与电压源电压”方程
例:列出图示电路的节点电压方程。 小结★:①对有伴电压源将它等 效电流源与电阻并联的形式;② 对于无伴电压源,若其有一端接 参考点,则另一端的节点电压已 知,对此节点就不用列节点方程 了;否则在电压源上假设一电流, 并把它看成电流源,最后,补 “节点电压与电压源电压”方程 G1 G2 1 uS1 iS G3 2 3 4 uS2 uS3 G3 G3uS3 I 解:设节点电压分别为u1、u2、u3。 假设uS2上的电流为I,把它看成是 电流为I的电流源。列节点1和3的 方程为 G1u1 – G1u2 = iS – I (G2 + G3 ) u3 – G2u2 = I + G3 u3 对uS2补一方程:u1 – u3 = uS2 二、特殊情况处理 6 2.4 节点法 1、电压源的处理方法 ①有伴电压源uS3:串并等效。 ②无伴电压源uS1和uS2: u2= uS1

2.4节点法 二、特殊情况处理 2、受控源的处理方法 2① 例:如图(a)电路,用节点法求电流i1和i2。 解:受控源看成独立源,有伴电压源串并等效(b) 9 2 设独立节点电压为u和4,则可列出节点方 程组为 (1+1)4a-4,=9+1+2i1 2i1 (1+0.5)4-ua=-2i1 再将控制量用节点电压表示,即 i1=9-ua/1 解得: w2=8V,4,=4V,i1=1A i2=4,/2=2(A) b 小结★:对受控源首先将它看成独立电源;列方程后,对每个受 控源再补一个方程将其控制量用节点电压表示
例:如图(a)电路,用节点法求电流i1和i2。 小结★ :对受控源首先将它看成独立电源;列方程后,对每个受 控源再补一个方程将其控制量用节点电压表示。 1Ω 2i1 i1 9V 1A 1Ω 2Ω a b i2 (a) 设独立节点电压为ua和ub,则可列出节点方 程组为 (1+1) ua – ub= 9 + 1 + 2 i1 (1+ 0.5) ub – ua= – 2 i1 再将控制量用节点电压表示,即 i1 = 9 – ua /1 解得: ua = 8V, ub = 4V, i1 = 1A i2 = ub /2 = 2(A) 1Ω 2i1 i1 9A (b) 1A 1Ω 2Ω a b i2 解:受控源看成独立源,有伴电压源串并等效(b) 7 2.4 节点法 二、特殊情况处理 2、受控源的处理方法
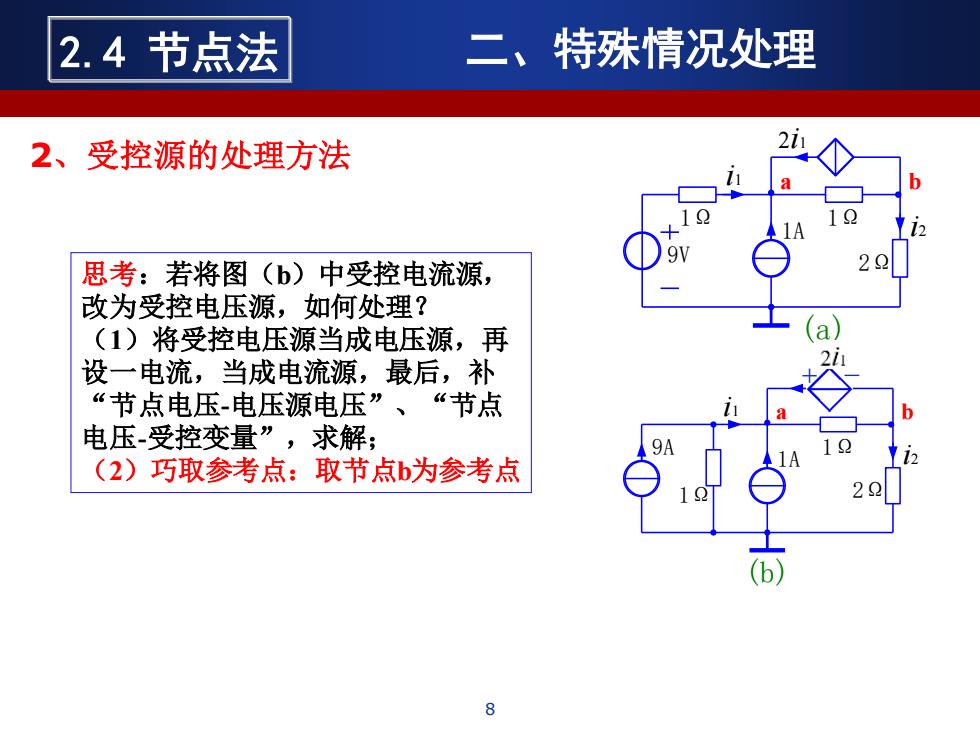
2.4节点法 二、特殊情况处理 2、受控源的处理方法 2 思考:若将图(b)中受控电流源, 改为受控电压源,如何处理? (1)将受控电压源当成电压源,再 设一电流,当成电流源,最后,补 “节点电压电压源电压”、“节点 电压受控变量”,求解; Q (2)巧取参考点:取节点b为参考点 8
思考:若将图(b)中受控电流源, 改为受控电压源,如何处理? (1)将受控电压源当成电压源,再 设一电流,当成电流源,最后,补 “节点电压-电压源电压”、“节点 电压-受控变量”,求解; (2)巧取参考点:取节点b为参考点 1Ω 2i1 i1 9V 1A 1Ω 2Ω a b i2 (a) 1Ω 2i1 i1 9A (b) 1A 1Ω 2Ω a b i2 8 2.4 节点法 二、特殊情况处理 2、受控源的处理方法 + _

2.5齐次定理和叠加定理 一、齐次定理 1、基本内容:对于具有唯一解的线性电路,当只有一个激 励源(独立电压源或独立电流源)作用时,其响应(电路任 意处的电压或电流)与激励成正比。 响应∝激励 X N 不含 不含 独立源 独立源 (a) (b) 。=KWs(常量K单位为S) i。=Ks(常量K无单位) 4。=K2s(常量K2无单位) u。=K,is(常量K单位为2)
uS (a) N0 不含 独立源 uo io iS (b) N0 不含 独立源 uo io io = K1uS (常量K1单位为S) uo= K2uS (常量K2无单位) io = K3 iS (常量K3无单位) uo= K4 iS (常量K4单位为Ω) 1、基本内容:对于具有唯一解的线性电路,当只有一个激 励源(独立电压源或独立电流源)作用时,其响应(电路任 意处的电压或电流)与激励成正比。 2.5 齐次定理和叠加定理 一、齐次定理 9 响应∝激励

2.5齐次定理和叠加定理 齐次定理 例:如图电路,N是不含独立源的线性电路,当Us=100V时, I=3A,U2=50V,R3的功率P3=60W,今若Us降为90V,试 求相应的红1'、U2和P3'。 解:激励降为原来的90/100=0.9倍,所以有: L1’=0.9I=0.9X3=2.7A; U2'=0.9U2=0.9X50=45V; P3'=U3'3'=0.9U3×0.9L =0.81U33=0.81P3=48.6W 10
例:如图电路,N是不含独立源的线性电路,当US=100V时, I1=3A,U2=50V,R3的功率P3= 60 W,今若US降为90V,试 求相应的I1 ’ 、U2 ’和P3 ’ 。 解:激励降为原来的90/100 = 0.9倍,所以有: I1 ’=0.9 I1= 0.9×3 =2.7A; U2 ’= 0.9 U2= 0.9×50 =45V; P3 ’=U3 ’I3 ’ =0.9U3 ×0.9I3 = 0.81U3 I3 = 0.81P3 = 48.6W US N U2 R1 I1 R3 R2 2.5 齐次定理和叠加定理 一、齐次定理 10