
历要毛子绑技大学 XIDIAN UNIVERSITY 1()1 mo I.电阻电路模块(直流稳态) 第二章电阻电路分析
XiDian I. 电阻电路模块(直流稳态) 第二章 电阻电路分析

第二章目录 2.1图与电路方程 2.22b法和支路法 2.3回路法和网孔法 电路方程分析法 2.4节点法 2.5 齐次定理和叠加定理 2.6替代定理 电路定理 2.7等效电源定理 2.8特勒根定理和互易定理 2-42-52-62-72-182-212-242-262-272-292-30
第二章 目 录 ❖2.1 图与电路方程 ❖2.2 2b法和支路法 ❖2.3 回路法和网孔法 ❖2.4 节点法 ❖2.5 齐次定理和叠加定理 ❖2.6 替代定理 ❖2.7 等效电源定理 ❖2.8 特勒根定理和互易定理 2-4 2-5 2-6 2-7 2-18 2-21 2-24 2-26 2-27 2-29 2-30 电路方程分析法 电路定理

2.22b法和支路法 一、2b法 一、2b法 对于n个节点、b条支路的电路 待求变量:b条支路电压+b条支路电流=2b 电路方程:(n-1)个KCL独立方程 +(b-n+1)个KVL独立方程 +b个元件VAR方程 =2b
3 一、2b法 对于n个节点、b条支路的电路 待求变量:b条支路电压 + b条支路电流 = 2b 电路方程: (n – 1)个KCL独立方程 + (b – n + 1)个KVL独立方程 + b个元件VAR方程 = 2b 2.2 2b法和支路法 一、2b法

2.22b法和支路法 二、支路法(b法) 二、支路法 1、支路法:以支路电流(或支路电压)为未知变量列出方程, 求解支路电流(或支路电压)。 2、步骤:(以支路电流法为例说明)》 ()、选定各支路电流的参考方向: (2)、对(n-1)个独立节点,列出独立KCL方程; (3)、选定(b-n+1)个独立回路,指定回路绕行方向,根据KVL和OL列 出回路电压方程。列写过程中将支路电压用支路电流来表示。 (4)、联立求解上述b个支路电流方程; (⑤)、进而求题中要求的支路电压或功率等
4 2.2 2b法和支路法 二、支路法(b法) 1、支路法:以支路电流(或支路电压)为未知变量列出方程, 求解支路电流(或支路电压)。 二、支路法 2、步骤:(以支路电流法为例说明) ⑴、选定各支路电流的参考方向; ⑵、对(n-1)个独立节点,列出独立KCL方程; ⑶、选定(b-n+1)个独立回路,指定回路绕行方向,根据KVL和OL列 出回路电压方程。列写过程中将支路电压用支路电流来表示。 ⑷、联立求解上述b个支路电流方程; ⑸、进而求题中要求的支路电压或功率等

2.3 回路法与网孔法 回路法★ 1、回路法:以一组独立回路电流为电路变量,并对独立回路用KVL 列出用回路电流表达有关支路电压的方程的求解方法。 独立回路:基本回路或网孔(网孔法) 列写方程个数:b-n+1 2、回路电流 在每个独立回路中假想有一个电流在回路中环流一周,而各支 路电流看作是由独立回路电流合成的结果。回路的巡行方向也是回 路电流的方向。 注意:回路电流是一种假想的电流,实际电路中并不存在。引 入回路电流纯粹是为了分析电路方便
5 2.3 回路法与网孔法 2、回路电流 在每个独立回路中假想有一个电流在回路中环流一周,而各支 路电流看作是由独立回路电流合成的结果。回路的巡行方向也是回 路电流的方向。 注意:回路电流是一种假想的电流,实际电路中并不存在。引 入回路电流纯粹是为了分析电路方便。 1、回路法:以一组独立回路电流为电路变量,并对独立回路用KVL 列出用回路电流表达有关支路电压的方程的求解方法。 独立回路:基本回路或网孔(网孔法) 一、回路法★ 列写方程个数:b – n + 1
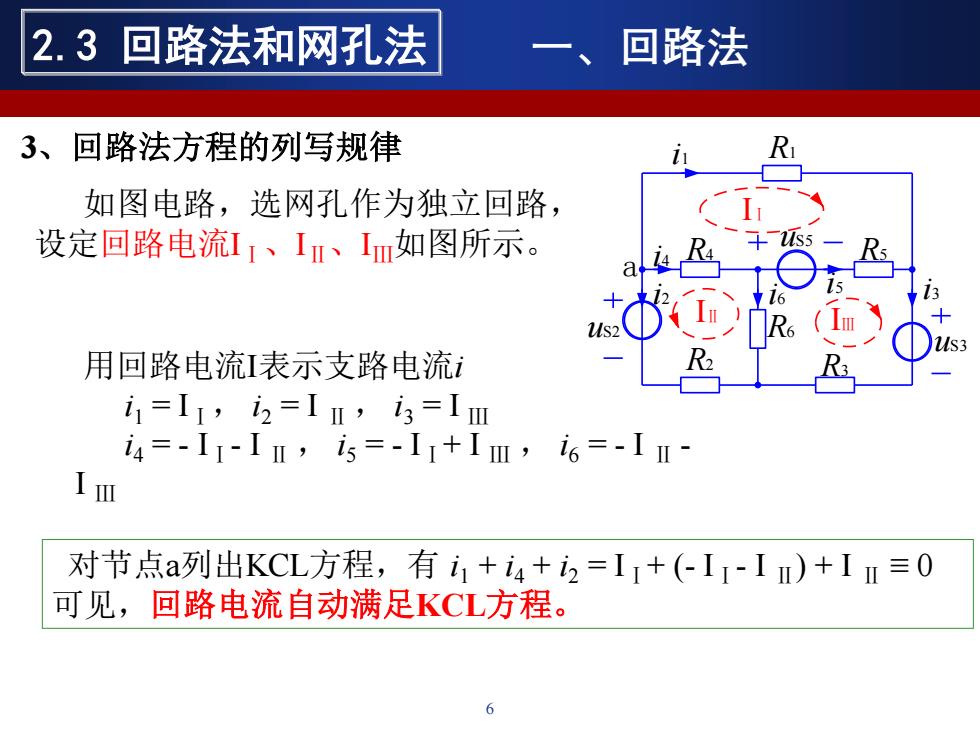
2.3回路法和网孔法 回路法 3、回路法方程的列写规律 如图电路,选网孔作为独立回路, 设定回路电流I1、I、m如图所示。 a 4S5 s2( R 用回路电流I表示支路电流1 R i1=I1,i2=IⅡ,3=Im i4=-I1IⅡ,is=-I1+Im,i6=-Im- 工西 对节点a列出KCL方程,有i1+i4+2=I,+(Ir-I)+IⅡ≡0 可见,回路电流自动满足KCL方程
6 2.3 回路法和网孔法 一、回路法 如图电路,选网孔作为独立回路, 设定回路电流IⅠ、IⅡ、IⅢ如图所示。 i4 R1 uS5 R2 R3 R4 R5 R6 uS3 uS2 IⅠ i1 i2 i3 i5 i6 IⅡ IⅢ a 用回路电流I表示支路电流i i1 = IⅠ, i2 = I Ⅱ , i3 = I Ⅲ i4 = - IⅠ- I Ⅱ , i5 = - IⅠ+ I Ⅲ , i6 = - I Ⅱ - I Ⅲ 对节点a列出KCL方程,有 i1 + i4 + i2 = IⅠ+ (- IⅠ- I Ⅱ) + I Ⅱ ≡ 0 可见,回路电流自动满足KCL方程。 3、回路法方程的列写规律

2.3回路法和网孔法 回路法 利用KVL和OL列出三个独立回路的KVL (I)R1i1-Rsis-uss-Rai4=0 (IⅡ)us2+R22-R6i6-R4i4=0 (I)uss+Rsis+us3+R3i3-R6i6=0 a4飞 1s5 将支路电流用回路电流表示,并代入上式, 6 (I)RII-R5(-I1+I)-us5-R4(-II-II)=0 R2 (I)us2+R2IⅡ-R6(IⅡ-Im)-R4(-II-II)=0 (I)uss+R5(-I1+Im)+us3+R3II-R6(-I II-II)=0 整理得: (I)(R1+R4+R5)II+ R4IⅡ- RsI mI=us5 Ru R12 R13 (ZUs) (IⅡ) RaII +(R2+R6+R4)IⅡ+ R6I mII=-us2 R21 R22 R23 (Us)2 () -R5II R6I II+(R5+R3+R6)I II=-uss-us3 R31 R32 R33 (ZUs)3
7 利用KVL和OL列出三个独立回路的KVL (Ⅰ) R1 i1 – R5 i5 – uS5 – R4 i4 = 0 (Ⅱ) uS2+ R2 i2 – R6 i6 – R4 i4 = 0 (Ⅲ) uS5 + R5 i5 + uS3 + R3 i3 – R6 i6 = 0 i4 R1 uS5 R2 R3 R4 R5 R6 uS3 uS2 IⅠ i1 i2 i3 i5 i6 IⅡ IⅢ a 将支路电流用回路电流表示,并代入上式 (Ⅰ) R1 IⅠ– R5 (- IⅠ+ I Ⅲ) – uS5 – R4 (- IⅠ- I Ⅱ) = 0 (Ⅱ) uS2 + R2 I Ⅱ - R6 (- I Ⅱ - I Ⅲ) – R4 (- IⅠ- I Ⅱ) = 0 (Ⅲ) uS5 + R5 (- IⅠ+ I Ⅲ) + uS3 + R3 I Ⅲ – R6 (- I Ⅱ - I Ⅲ) = 0 整理得: (Ⅰ) (R1 +R4 + R5 )IⅠ + R4 I Ⅱ – R5 I Ⅲ = uS5 (Ⅱ) R4 IⅠ + (R2 +R6 + R4 ) I Ⅱ + R6 I Ⅲ = - uS2 (Ⅲ) – R5 IⅠ + R6 I Ⅱ + (R5 +R3 + R6 )I Ⅲ = - uS5 - uS3 R11 R22 R33 R12 R13 R21 R23 R31 R32 (∑US )1 (∑US )2 (∑US )3 2.3 回路法和网孔法 一、回路法

2.3回路法和网孔法 回路法 由电路直接列写回路方程的规律总结 R(=I,IⅡ,)称为回路的自电阻=第个回路所有电阻之 和,恒取正; R,称为回路与回路的互电阻=回路与回路共有支路上 所有公共电阻的代数和;若流过公共电阻上的两回路电 流方向相同,则前取“+”号;方向相反,取“”号。 (∑Us):称为回路的等效电压源=回路中所有电压源电压 升的代数和。即,当回路电流从电压源的“+”端流出 时,该电压源前取“+”号;否则取
8 Rii(i=Ⅰ,Ⅱ,Ⅲ)称为回路i的自电阻=第i个回路所有电阻之 和,恒取正; Rij称为回路i与回路j的互电阻=回路i与回路j共有支路上 所有公共电阻的代数和;若流过公共电阻上的两回路电 流方向相同,则前取“+”号;方向相反,取“-”号。 (∑US ) i 称为回路i的等效电压源=回路i中所有电压源电压 升的代数和。即,当回路电流从电压源的“ + ”端流出 时,该电压源前取“+ ” 号;否则取“ - ” 。 由电路直接列写回路方程的规律总结 2.3 回路法和网孔法 一、回路法

2.3回路法和网孔法 回路法 4、回路法步骤: (1) 选定一组(b-n+1)个独立回路(大白话:“眼”数 个独立回路),并标出各回路电流的参考方向。 (2)以回路电流的方向为回路的巡行方向,按照前 面总结的规律列出各回路电流方程。 (3)联立求解,解出各回路电流。 (4)根据回路电流再求其它待求量
9 (2)以回路电流的方向为回路的巡行方向,按照前 面总结的规律列出各回路电流方程。 (3)联立求解,解出各回路电流。 (4)根据回路电流再求其它待求量。 (1)选定一组(b-n+1)个独立回路(大白话:“眼”数 个独立回路),并标出各回路电流的参考方向。 4、回路法步骤: 2.3 回路法和网孔法 一、回路法
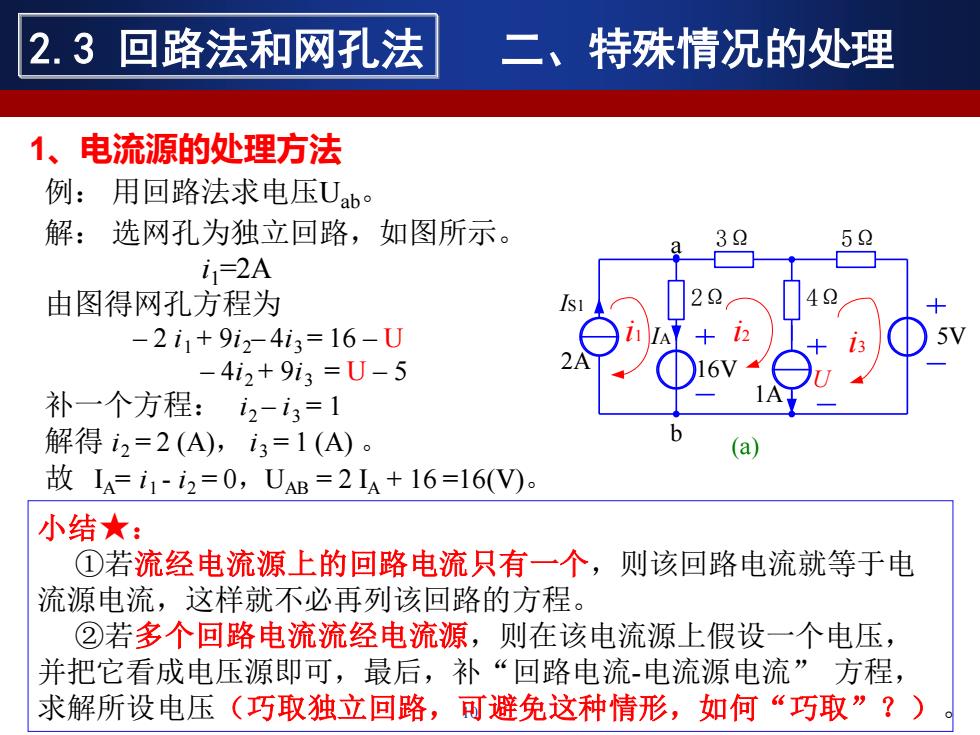
2.3回路法和网孔法 二、特殊情况的处理 1、电流源的处理方法 例:用回路法求电压Uab。 解:选网孔为独立回路,如图所示。 32 52 i1=2A 由图得网孔方程为 s -2i1+9i24i3=16-U -4i2+9i3=U-5 补一个方程:2-13=1 解得i2=2(A),i3=1(A)。 故I=i1-i2=0,UAB=2Ia+16=16(V)。 小结★: ①若流经电流源上的回路电流只有一个,则该回路电流就等于电 流源电流,这样就不必再列该回路的方程。 ②若多个回路电流流经电流源,则在该电流源上假设一个电压, 并把它看成电压源即可,最后,补“回路电流-电流源电流”方程, 求解所设电压(巧取独立回路,可避免这种情形,如何“巧取”?)
二、特殊情况的处理 10 例: 用回路法求电压Uab。 a b IS1 2A 16V 3Ω 2Ω 1A 4Ω 5Ω i1 i2 i3 5V (a) U IA 解: 选网孔为独立回路,如图所示。 i1=2A 由图得网孔方程为 – 2 i1 + 9i2– 4i3 = 16 – U – 4i2 + 9i3 = U – 5 补一个方程: i2 – i3 = 1 解得 i2 = 2 (A), i3 = 1 (A) 。 故 IA= i1 - i2 = 0,UAB = 2 IA + 16 =16(V)。 小结★: ①若流经电流源上的回路电流只有一个,则该回路电流就等于电 流源电流,这样就不必再列该回路的方程。 ②若多个回路电流流经电流源,则在该电流源上假设一个电压, 并把它看成电压源即可,最后,补“回路电流-电流源电流” 方程, 求解所设电压(巧取独立回路,可避免这种情形,如何“巧取”?)。 1、电流源的处理方法 2.3 回路法和网孔法