
4.7变压器 理想变压器 (3) 变阻特性: NIN2 如图理想变压器,在正孩稳态条 件下,其VAR的相量形式为 02=nU2 a -N2 N 若次级接负载阻抗乙,则由初级端口看的输入阻抗 NLU2 01= N2 N N2 -i2) U2 由= 理想变压器的阻抗变换作用只改变 in ZL=n2Z 阻抗的大小,且与同名端无关
(3)变阻特性: 如图理想变压器,在正弦稳态条 件下,其VAR的相量形式为 N1:N2 U1 U2 1 I 2 I ZL 2 2 1 2 1 2 2 2 1 1 1 I n I N N I U nU N N U = − = − = = 若次级接负载阻抗ZL,则由初级端口看的输入阻抗 ( ) 2 2 2 2 1 2 1 2 2 2 1 1 1 I U N N I N N U N N I U Zin − = − = = 由于ZL= 2 2 I U − i n Z L n Z L N N Z 2 2 2 1 = = = U1 1 I n Z L 2 理想变压器的阻抗变换作用只改变 阻抗的大小,且与同名端无关。 4.7 变压器 一、理想变压器
4.7变压器 理想变压器 两种等效关系: N 证: i1=d2-Z,i) N 设次级中的阻抗2,转移到初级里阻抗为配,有 0-2h-Un N2 联立求解得 N2 2Z2
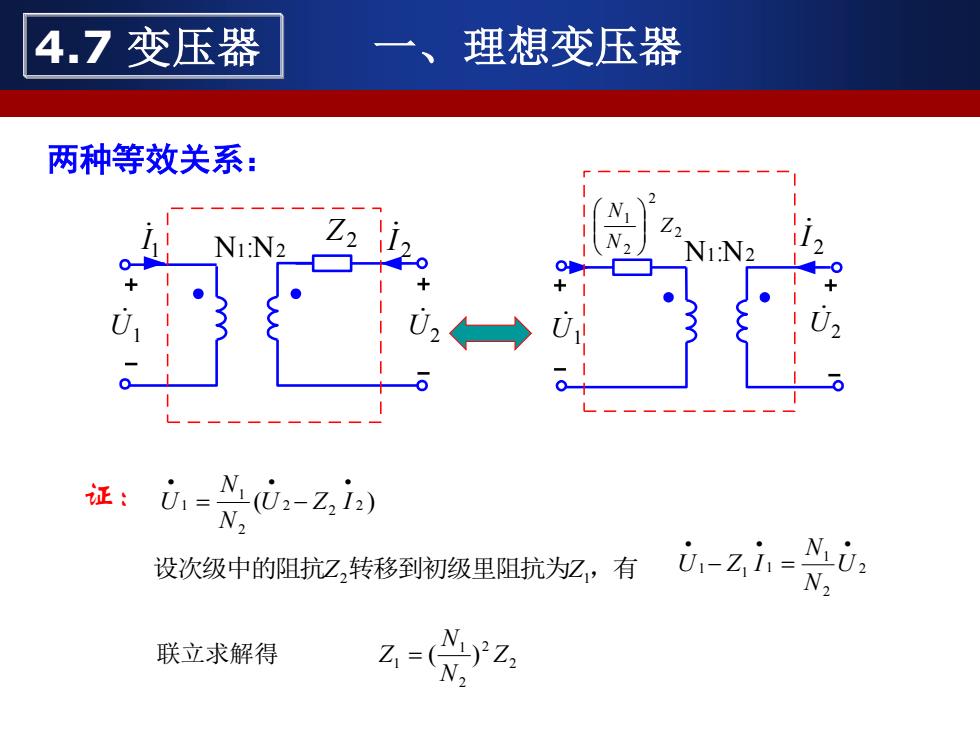
两种等效关系: N1:N2 U1 U2 1 I 2 I Z2 N1:N2 U1 U2 2 I 2 2 2 1 Z N N ( 2 ) 2 2 2 1 1 • • • = U − Z I N N U 设次级中的阻抗Z2转移到初级里阻抗为Z1,有 2 2 1 1 1 1 • • • − = U N N U Z I 联立求解得 2 2 2 1 1 ( ) Z N N Z = 证: 4.7 变压器 一、理想变压器
4.7变压器 理想变压器 例1已知图(a)示正孩稳态电路中Us=50∠0°V,变比n=2, 求电流i和负载RL消耗的平均功率PL 5I n】 解变压器初级等效输入电阻为 Rn=n2R=22×5=202如(b)图 根据KV儿方程,有 -j25 (5+Rn-j25)i1=Us (a) Us 50 1=5+Rmj2525-J25 V2∠45°A 521 R消耗的平均功率就是R消耗的功率,即 ①iRin020Q PL=I2Rin=2X20=40W j252 (b)
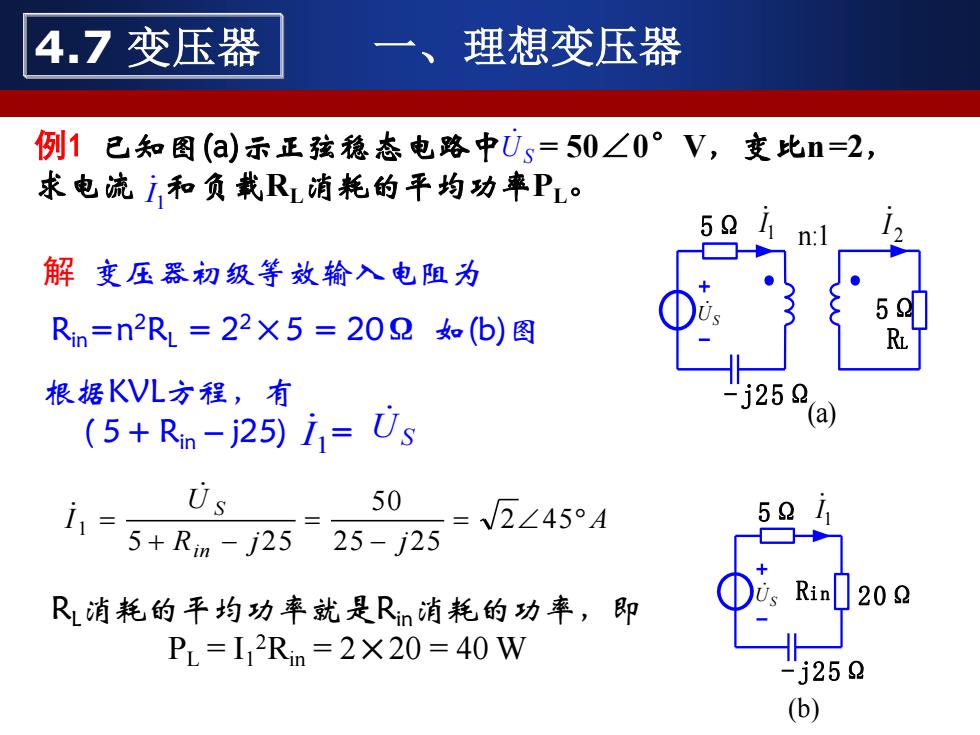
例1 已知图(a)示正弦稳态电路中 = 50∠0°V,变比n =2, 求电流 和负载RL消耗的平均功率PL。 n:1 US 1 I 2 I 5 Ω -j25Ω 5 Ω (a) RL 解 变压器初级等效输入电阻为 Rin=n2RL = 22×5 = 20Ω 如(b)图 US 1 I 20Ω -j25Ω 5 Ω (b) Ri n 根据KVL方程,有 ( 5 + Rin – j25) = 1 I US A R j j U I i n S = − = + − = 2 4 5 2 5 2 5 5 0 5 2 5 1 RL消耗的平均功率就是Rin消耗的功率,即 PL = I1 2Rin = 2×20 = 40 W 4.7 变压器 一、理想变压器 1 I US

4.7变压器 理想变压器 例2如图电路的相量模型,已知Us=4V,求理想电压表的读数。 解 i129 2:1 2 U2 LU:=2V 若次级接理想电流表,求电流表的读数。 2 i2=-2i1=-0s I2=Us=4A
例2 如图电路的相量模型,已知US = 4V,求理想电压表的读数。 U S V 1 I U1 2Ω 2:1 2 I U2 解 U US 2 1 2 = 2V 2 1 U2 = US = 若次级接理想电流表,求电流表的读数。 2 1 US I = US I I = − = − 2 2 1 I 2 =US = 4A 4.7 变压器 一、理想变压器

4.7变压器 理想变压器 例3已知Us=6∠0V求开路电压U a 2:1 解 0=s=320V 2 若求ab端短路,如何求其上的短 路电流? 3 0x=3d,-i)-3,-)=-32 U1=-2U2=-2UR 0s=0,+0e=-2Ue+0e=-Un-=号i, 2 h= 0s=4∠0°A 3
例3 已知 2:1 US U 3Ω a b U S = 60V 求开路电压 U 解 3 0 V 2 1 = = U US 若求ab端短路,如何求其上的短 路电流? 2 I + - U R 1 I + 1- U 1 2 2 1 I I = 1 2 2 2 2 2 3 ) 2 1 U 3(I I ) 3( I I I R = − = − = − U U U 1 2 = − = − 2 2 R 1 2 2 3 U U U 2U U U I S R R R R = + = − + = − = 4 0 A 3 2 2 = = US I 4.7 变压器 一、理想变压器 U2 + -

4.7变压器 二、全耦合变压器 若将两个线圈绕在高导磁率铁磁材料上,则可使两线圈的 耦合系数k接近1,当工作频率不太高时,线圈的损耗可忽略。 理想情况下,这种全耦合、无耗的耦合线圈称为全耦合变压器。 与理想变压器相比,只有L1、L2为∞的条件不满足。 图中全耦合互感线圈,其VAR关系为,。i k=1 41=L1 +4 di diz (1) dt z uz =L2 dt di dt (2) 前面已知,k=1时, 变压关系与理想 L 变压器相同 故 N2 M L2 L2 N2
若将两个线圈绕在高导磁率铁磁材料上,则可使两线圈的 耦合系数k接近1,当工作频率不太高时,线圈的损耗可忽略。 理想情况下,这种全耦合、无耗的耦合线圈称为全耦合变压器。 与理想变压器相比,只有L1、L2为∞的条件不满足。 u2 k=1 u1 L1 L2 图中全耦合互感线圈,其VAR关系为, i1 i2 2 1 2 1 2 1 L L L M M L N N = = = 前面已知,k=1时, n N N u u = = 2 1 2 1 故 变压关系与理想 变压器相同 t i L L t i u L t i L L t i u L d d d d d d d d 1 1 2 2 2 2 2 1 2 1 1 1 = + = + (1) (2) 4.7 变压器 二、全耦合变压器

4.7变压器 二、全耦合变压器 对式(I)从-∞到t积分,并设i1(-∞)=i2(-∞)=0,得 0=a(a-240=2xadr安0=60+40 N 式中, i6(t)= ∫'n4()dr 是由于存在初级自感L而出现的, L 称为励磁电流。 N2i20 是次级电流2在初级的反映,宅与i2之间满足 理想变压器的变流关华。 11 1'1 NI:N2 它是由理想变压器在其初级并 联电感L构成的。L1常称为励 磁电感
对式(1)从-∞到t积分,并设i1 (-∞)= i2 (-∞)=0,得 ( ) d ( ) ( ) ( ) 1 ( ) d ( ) 1 ( ) ' 2 1 1 2 1 1 2 1 2 1 1 1 i t i t i t N N u L i t L L u L i t t t = − = − = + − − 式中, − = t u L i t ( ) d 1 ( ) 1 1 是由于存在初级自感L1而出现的, 称为励磁电流。 '( ) ( ) 2 1 2 1 i t N N i t = − 是次级电流i2在初级的反映,它与i2之间满足 理想变压器的变流关系。 u2 N1:N2 u L1 1 i1 i'1 i2 它是由理想变压器在其初级并 联电感L1构成的。 L1常称为励 磁电感。 4.7 变压器 二、全耦合变压器
4.7变压器 三、实际铁心变压器模型 对于实际变压器,尽管采用导磁率较高的铁心(或磁心), 耦合得很紧,但耦合系数总小于1,而且不可避免地有损耗。 初级 初级漏电感 次级漏电感 次级 铜耗 铜耗 1 铁心损耗电 励磁电 感
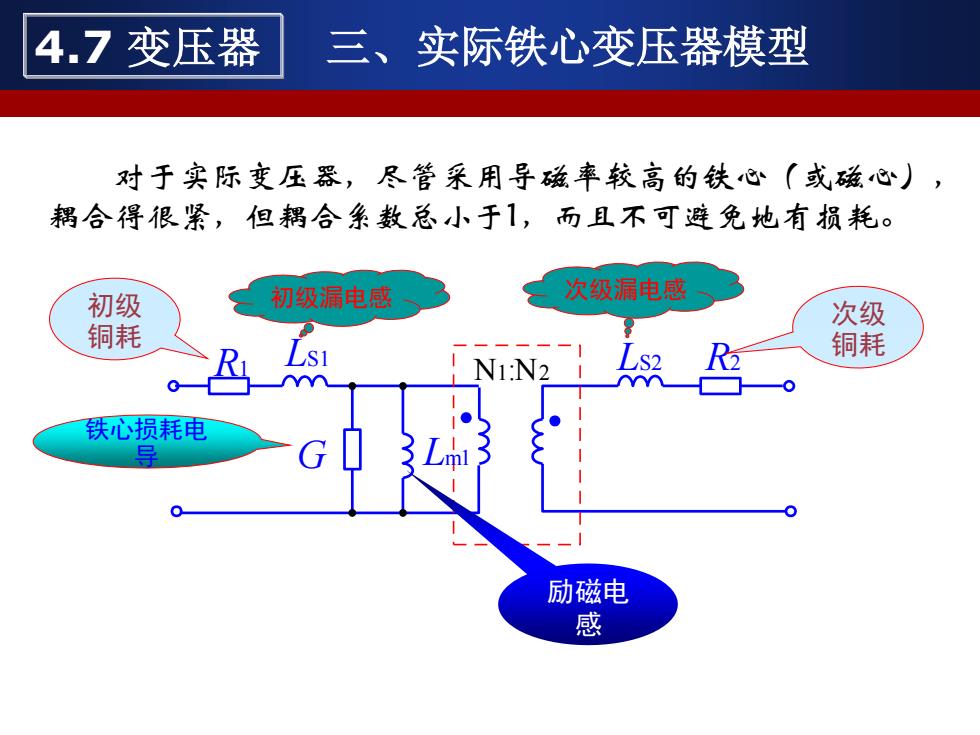
对于实际变压器,尽管采用导磁率较高的铁心(或磁心), 耦合得很紧,但耦合系数总小于1,而且不可避免地有损耗。 N1:N2 G R LS1 R2 1 LS2 Lm1 初级漏电感 次级漏电感 初级 铜耗 次级 铜耗 铁心损耗电 导 励磁电 感 4.7 变压器 三、实际铁心变压器模型