
1.7含独立源的等效 二、实际电源模型及其互换等效 1实际电源的模型(区别:实际电源有内阻) 一个实际电源端口上电压电流的关系VCR 际 也称为外特性。 电源 改变R,可以得到一组u,数值,描点可以 (a) 得到图b。 R=oo,开路,=0,u=Us(端口开路电压) (b) R=0,短路,u=0,i=s(端口短路电流) Us/Is=Rs u=Us -Rs i CR关系两种表达: i=Is -u/Rs
二、实际电源模型及其互换等效 1.实际电源的模型(区别:实际电源有内阻) 一个实际电源端口上电压电流的关系VCR 也称为外特性。 改变R,可以得到一组u,i数值,描点可以 得到图b。 R=∞, 开路, i=0,u = US (端口开路电压) R = 0, 短路, u=0 , i = IS (端口短路电流) 1 1.7含独立源的等效 i 实 际 电 源 u (a) u 0 i US IS (b) R US /IS = RS VCR关系两种表达: u = US - RS i i = IS - u /RS
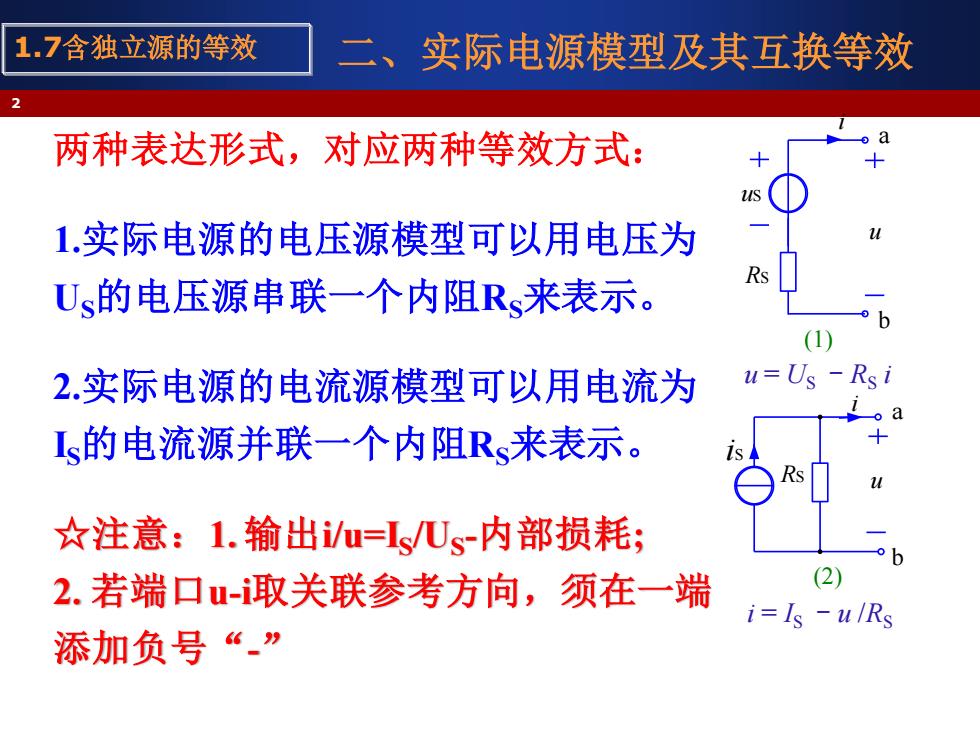
1.7含独立源的等效 实际电源模型及其互换等效 两种表达形式,对应两种等效方式: 1.实际电源的电压源模型可以用电压为 Us的电压源串联一个内阻Rs来表示。 (1) 2.实际电源的电流源模型可以用电流为 u=Us -Rs i Ls的电流源并联一个内阻Rs来表示。 RS ☆注意:1.输出i/u=Is/Us-内部损耗; 2.若端口u-i取关联参考方向,须在一端 (2) i=Is -u/Rs 添加负号
二、实际电源模型及其互换等效 两种表达形式,对应两种等效方式: 1.实际电源的电压源模型可以用电压为 US的电压源串联一个内阻RS来表示。 2.实际电源的电流源模型可以用电流为 IS的电流源并联一个内阻RS来表示。 ☆注意:1. 输出i/u=IS /US -内部损耗; 2. 若端口u-i取关联参考方向,须在一端 添加负号“-” 2 1.7含独立源的等效 i RS a u b uS (1) u = US - RS i i = IS - u /RS i iS RS u a b (2)
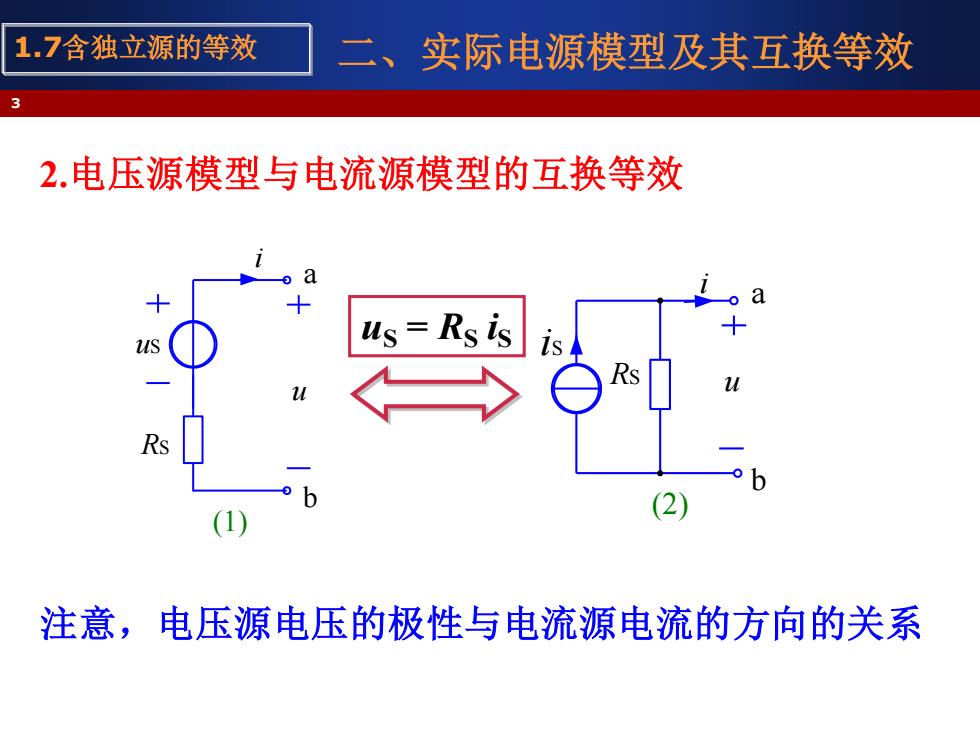
1.7含独立源的等效 二、实际电源模型及其互换等效 2.电压源模型与电流源模型的互换等效 a us=Rs is (2 注意,电压源电压的极性与电流源电流的方向的关系
二、实际电源模型及其互换等效 2.电压源模型与电流源模型的互换等效 注意,电压源电压的极性与电流源电流的方向的关系 3 1.7含独立源的等效 i RS a u b uS (1) i iS RS u a b (2) uS = RS iS
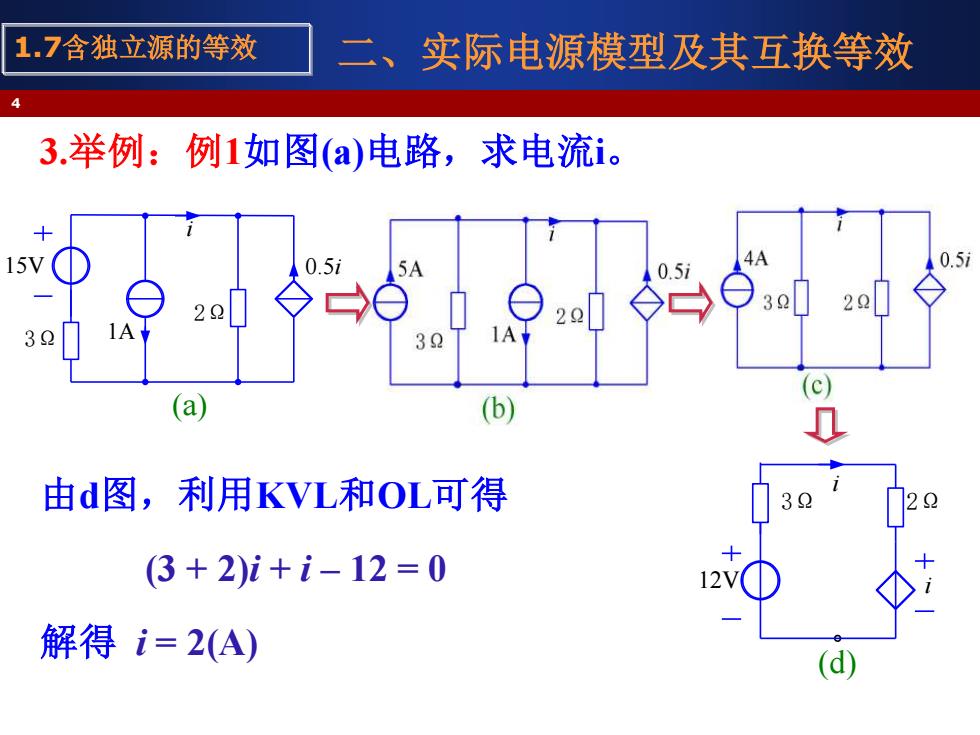
1.7含独立源的等效 二、 实际电源模型及其互换等效 3.举例:例1如图(a)电路,求电流i。 5A 40.5i 4A 22 30 3 (a) (b) 由d图,利用KVL和OL可得 (3+2)i+i-12=0 解得i=2(A)
二、实际电源模型及其互换等效 3.举例:例1如图(a)电路,求电流i。 由d图,利用KVL和OL可得 (3 + 2)i + i – 12 = 0 解得 i = 2(A) 4 1.7含独立源的等效 2Ω 3Ω i 15V (a) 1A 0.5i 3Ω 2Ω i 12V (d) i

1.7含独立源的等效 二、实际电源模型及其互换等效 例2:如图(a)电路,设 N2 1/A i2/A 二端电路N,和电路N2的 10 VCR特性如图示,求电 压ub(看图说话)。 (a) 解:N、N的外特性为 N2 45A i1=-5+0.5u 22 22 =2-0.5u 由d图可得: 5A4 Uab=4.5V 52 22
二、实际电源模型及其互换等效 例2:如图(a)电路,设 二端电路N1和电路N2的 VCR特性如图示,求电 压uab(看图说话)。 解:N1 、N2的外特性为 i1 = -5 + 0.5 u i2 = 2 - 0.5 u 由d图可得: uab = 4.5V 5 1.7含独立源的等效 (a) 10 u/V i1/A 0 N1 -5 2 u/V i2/A 0 4 2V 1Ω u u i1 i2 N2 a b (b) 5A 2Ω N1 2V 1Ω u u i1 i2 N2 2A 2Ω a b (c) 5A 2Ω 2A 1Ω u 2A 2Ω b a a u 9A b (d) 0.5Ω
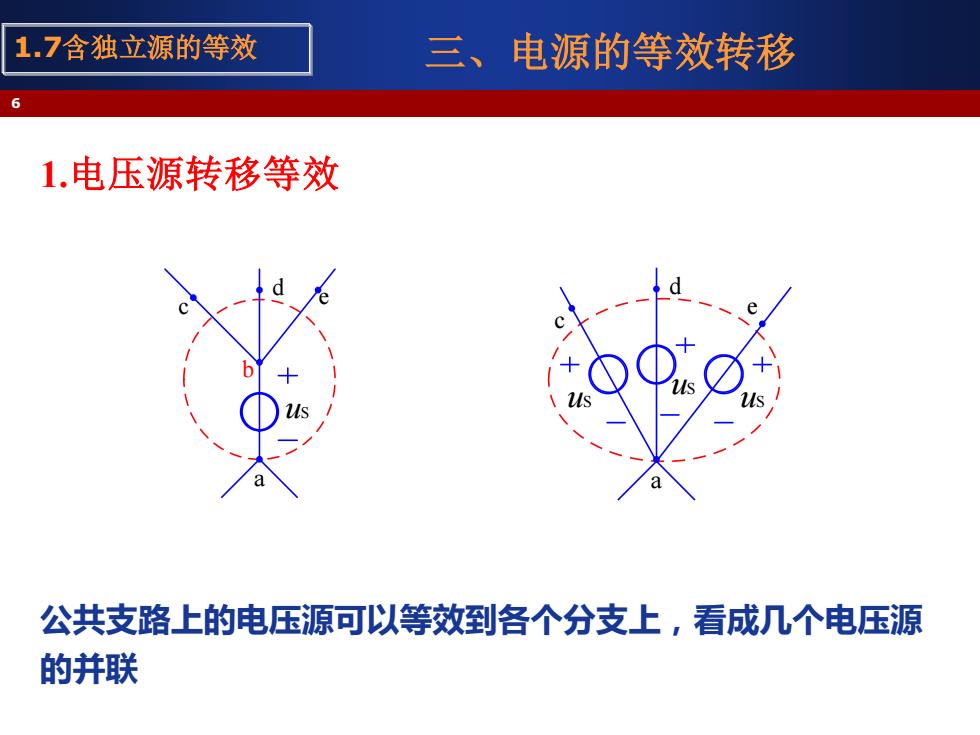
1.7含独立源的等效 三、电源的等效转移 1.电压源转移等效 公共支路上的电压源可以等效到各个分支上,看成几个电压源 的并联
三、电源的等效转移 1.电压源转移等效 公共支路上的电压源可以等效到各个分支上,看成几个电压源 的并联 6 1.7含独立源的等效 a b uS c d e d e a c uS uS uS

1.7含独立源的等效 三、电源的等效转移 4 例:如图所示电路,求电流i 解:1.如图所示有三个未知量, 12V 6 421 列写三个KVL, 12=3(i1+i)+6i1 i=0.4A 12=4(i2-i)+4i2 解得{i1=1.2A 6i1=i+4i2 i2=1.7A
三、电源的等效转移 例:如图所示电路,求电流i 解:1. 如图所示有三个未知量, 列写三个KVL, ቐ 12 = 3(𝑖1 + 𝑖) + 6𝑖1 12 = 4(𝑖2 − 𝑖) + 4𝑖2 6𝑖1 = 𝑖 + 4𝑖2 解得 ቐ 𝑖 = 0.4𝐴 𝑖1 = 1.2𝐴 𝑖2 = 1.7𝐴 7 1.7含独立源的等效 1 i
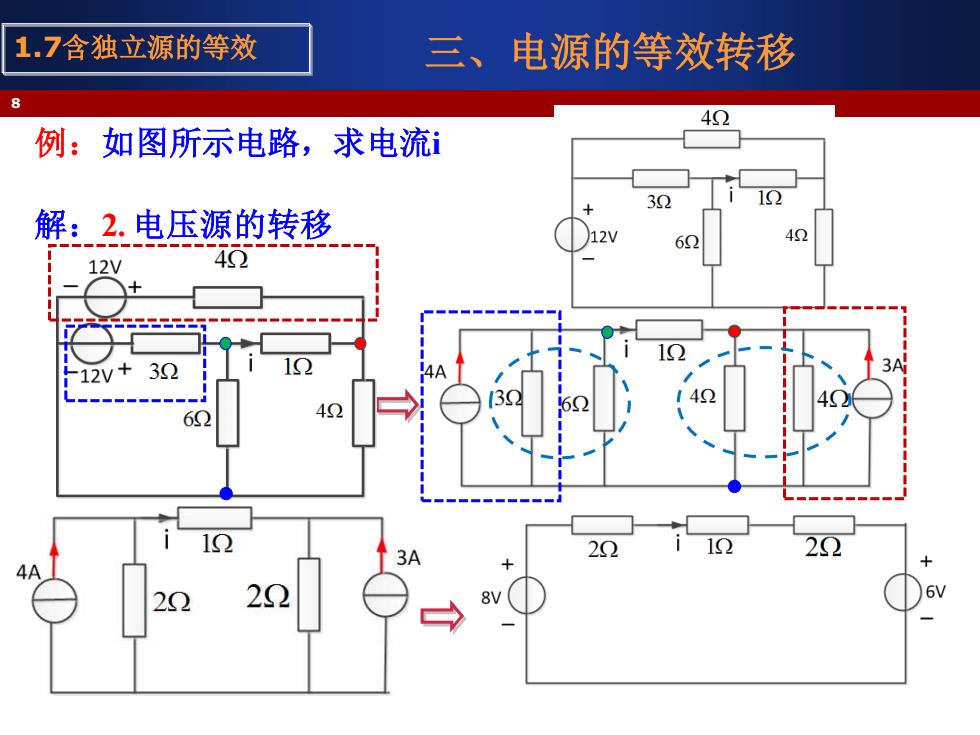
1.7含独立源的等效 三、电源的等效转移 4Q2 例:如图所示电路,求电流 3 1 解:2.电压源的转移 62 12V 4Ω 12V+32 6 42 4A
三、电源的等效转移 例:如图所示电路,求电流i 解:2. 电压源的转移 8 1.7含独立源的等效
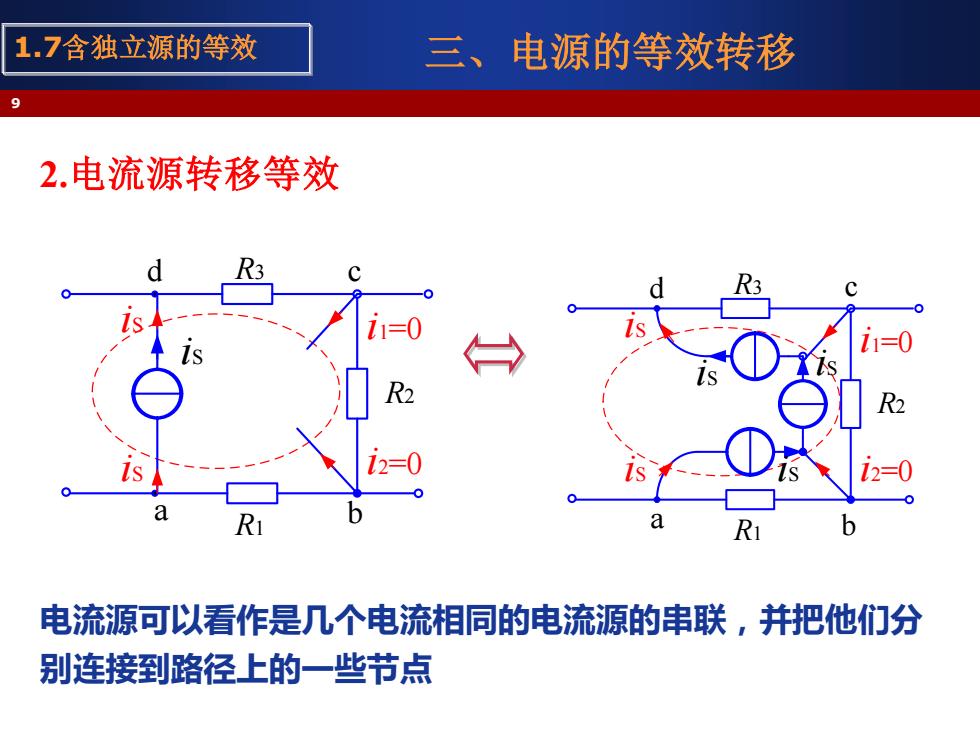
1.7含独立源的等效 三、电源的等效转移 2.电流源转移等效 D 电流源可以看作是几个电流相同的电流源的串联,并把他们分 别连接到路径上的一些节点
三、电源的等效转移 2.电流源转移等效 电流源可以看作是几个电流相同的电流源的串联,并把他们分 别连接到路径上的一些节点 9 1.7含独立源的等效 iS R1 R2 R3 iS iS i1=0 i2=0 a b d c iS R1 R2 R3 iS iS i1=0 i2=0 iS iS a b d c
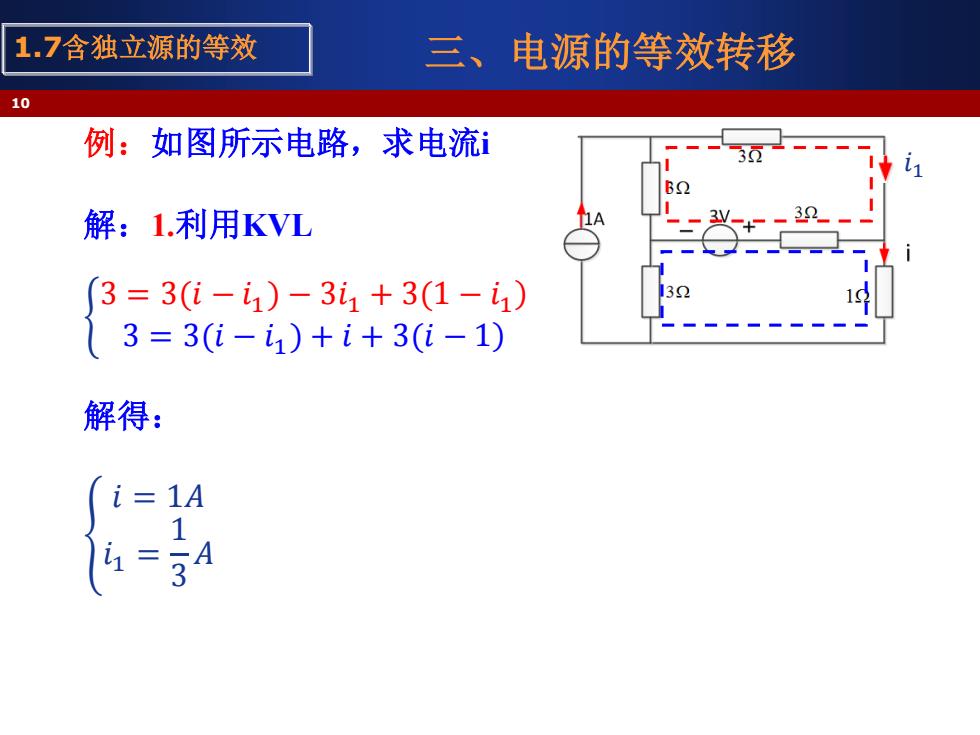
1.7含独立源的等效 三、电源的等效转移 10 例:如图所示电路,求电流 3 解:1.利用KVL +一 3=3(i-i1)-3i1+3(1-i1) {3=3(i-i1)+i+3(i-1) 解得: i=1A
三、电源的等效转移 例:如图所示电路,求电流i 解:1.利用KVL ቊ 3 = 3(𝑖 − 𝑖 ) 1 ) − 3𝑖1 + 3(1 − 𝑖1 3 = 3(𝑖 − 𝑖 ) 1 ) + 𝑖 + 3(𝑖 − 1 解得: ቐ 𝑖 = 1𝐴 𝑖1 = 1 3 𝐴 10 1.7含独立源的等效 𝑖1