
历竖毛子代技大学 XIDIAN UNIVERSITY 15 ood mo II.动态电路模块 第三章动态电路
XiDian II.动态电路模块 第三章 动态电路

目录 ÷3.1动态元件 动态元件的伏安关系及储能 3.2动态电路方程及其解 3.3电路的初始值 3.4动态电路的响应 零输入响应、零状态响应和全响应 3.5一阶电路的三要素公式 初始值、稳态值、时常数和三要素公式 %3.6一阶电路的阶跃响应 3-93-103-113-14.3-153-163-173-193-203-21 3-303-313-323-353-46
❖ 3.1 动态元件 动态元件的伏安关系及储能 ❖3.2 动态电路方程及其解 ❖3.3 电路的初始值 ❖3.4 动态电路的响应 零输入响应、零状态响应和全响应 ❖3.5 一阶电路的三要素公式 初始值、稳态值、时常数和三要素公式 ❖3.6 一阶电路的阶跃响应 目录 2 3-9 3-10 3-11 3-14 3-15 3-16 3-17 3-19 3-20 3-21 3-30 3-31 3-32 3-35 3-46
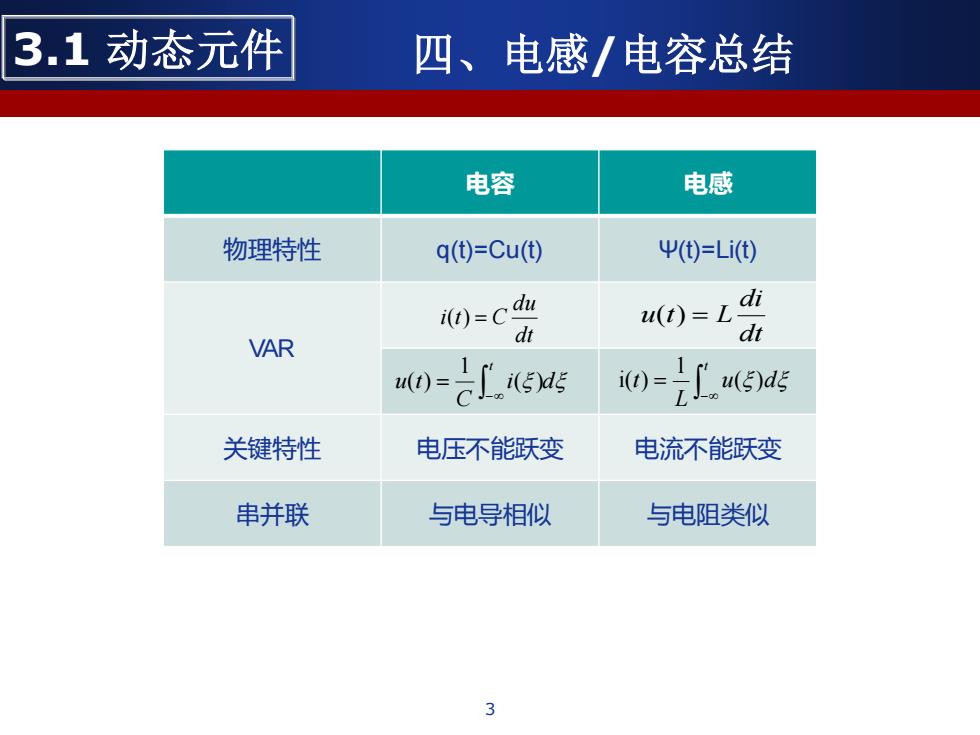
3.1动态元件 四、电感/电容总结 电容 电感 物理特性 q()=Cu(⑤) Ψ0)=Li) i(t)=cdu Ma0=l升 VAR w0=上A(6s 0=d 关键特性 电压不能跃变 电流不能跃变 串并联 与电导相似 与电阻类似 3
3.1 动态元件 四、电感/电容总结 3 电容 电感 物理特性 q(t)=Cu(t) Ψ(t)=Li(t) VAR 关键特性 电压不能跃变 电流不能跃变 串并联 与电导相似 与电阻类似 dt du i(t) = C i d C u t t − = ( ) 1 ( ) dt di u(t) = L − = t u d L t ( ) 1 i( )

3.2动态电路的方程及其解 一、动态电路方程 动态电路列出的方程是微分方程。若描述电路的方程是一阶微分方程, 相应的电路称为一阶电路(first order circuit)。 1、依据:元件VAR,KCL和KVL列写方程; 2、一阶电路举例: 例1:图RC电路,仁0时开关S闭合,讨论>0的电容电 压uc(t)。 >0时,根据KVL方程列出回路电压方程为R+c-s=0 RC串联电路 根据元件的VAR,有1=cd dt ,R=Ri=RCd di 代入上式,有 令=RC,其单位是秒: cdR+e-4,=0? dt dt RCuc -1 duc+ [RC]=[V/A][C/V]=[C/A]=[s], 为时间常数,简称时常数。 1 求解该一阶常微分方程即可 duc士二uc=二zM dt
3.2 动态电路的方程及其解 4 1、依据:元件VAR,KCL和KVL列写方程; 2、一阶电路举例: 动态电路列出的方程是微分方程。若描述电路的方程是一阶微分方程, 相应的电路称为一阶电路(first order circuit)。 例1:图RC电路,t=0时开关S闭合,讨论t>0的电容电 压uC(t)。 t>0时,根据KVL方程列出回路电压方程为 uR + uC – uS = 0 根据元件的VAR,有 代入上式,有 令τ=RC,其单位是秒: [RC]=[V/A][C/V]=[C/A]= [s], 为时间常数,简称时常数。 S uS uR uC R C i RC串联电路 d d , d d C C R u u i C u R i RC t t = = = 0 d d 1 1 d d C C C S C s u C u u u u t RC RC R t + = ? u - = + C S C u u t u 1 1 d d + = 一、动态电路方程 求解该一阶常微分方程即可

3.2动态电路的方程及其解 动态电路方程列写 例2:图RL电路,=0时开关S闭合,讨论>0时 的电感电流()。 >0时,根据KCL有R+L-is=0 根据元件的VAR,有 u:.=1.d iR=uL= L di RL并联电路 dt R =L/R(时间常数,简称时常 代入上式,整理得 dt L 数),单位秒。 [L/R]=[Wb/A]/[V/A]=[Wb/V]=[s] +二i 其中Wb=Volt×s dt 观察上两例列出的方程,除变量不同外,均为典型的一阶微分方程, 因此均为一阶电路。一阶微分方程的一般形式可写为 y(①)+a)=bf),式中y0为响应,f)为激励。 5
一、 动态电路方程列写 5 3.2 动态电路的方程及其解 例2:图RL电路,t=0时开关S闭合,讨论t>0时 的电感电流iL (t)。 t>0时,根据KCL有 iR + iL – iS = 0 根据元件的VAR,有 代入上式,整理得 观察上两例列出的方程,除变量不同外,均为典型的一阶微分方程, 因此均为一阶电路。一阶微分方程的一般形式可写为 y’(t) + ay(t) = bf (t), 式中y(t)为响应,f (t)为激励。 τ=L/R(时间常数,简称时常 数),单位秒。 [L/R]=[Wb/A]/[V/A]=[Wb/V]=[s] 其中Wb=Volt×s RL并联电路 S iS iR iL R L uL t i R L R u i t i u L L L R L L d d , d d = = = L S L i L R i L R t i + = d d L S L i i t i 1 1 d d + =

3.2动态电路的方程及其解 动态电路方程列写 3、二阶电路举例: 例:图RLC串联电路,仍以电容电压uc(① +R-+L- 作为电路的响应。 i 根据KVL方程有 uR +ul uc-us=0 C 根据元件的VAR,有 i=C duc dt dt2 代入上式,整理得 dt2L dt us 这是二阶微分方程,因此称该电路为二阶电路。二阶微分方程的一 般形式可写为 x(t)+av'(t)+aav(t)=bof(t) 6
6 3.2 动态电路的方程及其解 一、 动态电路方程列写 3、二阶电路举例: 例:图RLC串联电路,仍以电容电压uC(t) 作为电路的响应。 根据KVL方程有 uR + uL + uC – uS = 0 根据元件的VAR,有 代入上式,整理得 这是二阶微分方程,因此称该电路为二阶电路。二阶微分方程的一 般形式可写为 y”(t) + a1y’(t) + a0y(t) = b0 f (t) uS uR uC R C i uL L 2 2 d d , d d d d , d d C C C R L u u i t i u u L LC t C u R RC t t = = = i = = C S C C u LC u t LC u L R t u 1 1 d d d d 2 2 + + =

3.2动态电路的方程及其解 、 动态电路方程列写 4、建立动态方程的一般步骤 1 根据电路建立KCL或KVL方程; ② 写出个元件的伏安关系; ③ 在以上方程中消去中间变量,得到所需变量的微分 方程。 对于较复杂的动态电路,常用拉普拉斯变换进行分析
7 3.2 动态电路的方程及其解 一、 动态电路方程列写 4、建立动态方程的一般步骤 ① 根据电路建立KCL或KVL方程; ② 写出个元件的伏安关系; ③ 在以上方程中消去中间变量,得到所需变量的微分 方程。 对于较复杂的动态电路,常用拉普拉斯变换进行分析

3.2动态电路的方程及其解 二、 微分方程的解 1、微分方程的经典解法 一阶和二阶微分方程一般形式为 y'(t)+ay(t)=bf(t) (1),y”(t)+ay'()+ay)=boft) (2) 线性时不变动态电路的电路方程为线性常系数微分方程,解由两部分组成: y()=y()+y() 即:完全解=齐次解(通解)+特解 齐次解y(t):函数形式取决于微分方程的特征根。 ●一阶微分方程的特征方程为s+a=0,特征根为s=-a,故 yh(t)=K est=K e-at 式中K为待定常数,由初始条件(初始状态)决定。 二阶微分方程的特征方程为s2+a1s+a=0,特征根为s1和s2, 。 当s1fs2时,y()=K1est+K2es2t 当s1=S2=S时,yh()=(K1+K2t)est 式中待定常数K1、K2将在完全解中由初始条件(初始状态)确定
8 3.2 动态电路的方程及其解 二、 微分方程的解 1、微分方程的经典解法 一阶和二阶微分方程一般形式为 y’(t) + ay(t) = bf (t) (1) , y”(t) + a1y’(t) + a0y(t) = b0 f (t) (2) 线性时不变动态电路的电路方程为线性常系数微分方程,解由两部分组成: y(t) = yh (t) + yp (t) 即:完全解 =齐次解(通解)+ 特解 齐次解yh(t) :函数形式取决于微分方程的特征根。 ⚫ 一阶微分方程的特征方程为 s + a = 0,特征根为s = -a,故 yh (t) = K e st = K e-a t 式中K为待定常数,由初始条件(初始状态)决定。 ⚫ 二阶微分方程的特征方程为 s 2 + a1 s + a0 = 0,特征根为s1 和s2 , • 当s1 ≠s2 时, yh (t) = K1 e s1t + K2 e s2t • 当s1 = s2 = s时, yh (t) = (K1 + K2 t)e st 式中待定常数K1、 K2将在完全解中由初始条件(初始状态)确定

3.2动态电路的方程及其解 二 微分方程的解 特解y():特解具有与激励ft)相同的函数形式。列表如下:(P140表3-2) 激励f(t)函数形式 特解y) 直流 常数A tm Amtm+Am-itm-1+.+Ait+Ao Aeat 当a不是特征根时 eat (At+Ao)eat 当a是特征单根时 (A,t2+At+Ao)eat 当a是二阶特征根(二阶电路) cosβt 或 sinβt A,cosβt+A2sinβt 当特解y,(①)的函数形式确定后,将其代入原微分方程中,来求待定常数A 9
9 3.2 动态电路的方程及其解 二、 微分方程的解 特解yh (t) :特解具有与激励f(t)相同的函数形式。列表如下:(P140表3-2) 激励f(t)函数形式 特解yp (t) 直流 常数A t m Amt m+ Am-1 t m-1+.+ A1 t + A0 e αt Aeαt 当α不是特征根时 (A1 t + A0 )eαt 当α是特征单根时 (A2 t 2 +A1 t + A0 )eαt 当α是二阶特征根(二阶电路) cosβt 或 sin βt A1 cosβt+ A2 sin βt 当特解yp (t)的函数形式确定后,将其代入原微分方程中,来求待定常数Ai

3.2动态电路的方程及其解 二、 微分方程的解 2、举例如图RC电路,Us为直流电压源,当t=0时开关闭合,电容的初 始电压ucO)=Uo,求≥0时的uc()。 解(1)建立电路方程。前面己得 1 (2)求齐次解uCh()。特征方程为s+1/RC)=0 其特征根s=1V(RC),故,=Ke”=KeC RC串联电路 (3)求特解uc,①)。激励Us为常数,.特解也是常数。 令40=A,将它代入上面微分方程,得RCA=RCU, 故得特解uc,()=A=Us (4)求完全解uc(0)。hc()=uch)+cp(①)=KeRc'+Us 常数K由初试条件uc(O)=U,确定:uc(0)=K+Us=U,解得K=U-Us u()=(U。-Us)ec+U3,t≥0 10
10 3.2 动态电路的方程及其解 二、 微分方程的解 2、举例如图RC电路,Us为直流电压源,当t = 0时开关闭合,电容的初 始电压uC(0) = U0,求t≥0时的uC(t)。 解(1)建立电路方程。前面已得 (2)求齐次解uCh(t)。特征方程为s + 1/(RC) = 0 其特征根 s = - 1/(RC),故 (3)求特解uCp(t)。∵激励Us为常数,∴特解也是常数。 令 uCp(t) = A,将它代入上面微分方程,得 故得特解 uCp(t) = A = Us (4)求完全解uC (t)。 uC (t) = uCh(t) + uCp(t) = 常数K由初试条件uC (0) = U0确定: uC(0) = K + Us = U0 ,解得 K = U0 - Us C S C U RC u t RC u 1 1 d d + = t st RC uCh K K 1 e e − = = US RC A RC 1 1 = 1 e t R C K US - + ( ) ( ) e , 0 1 = 0 − + − u t U U U t S t RC C S S US uR uC R C i RC串联电路