
知识点回顾 1.本章研究对象? 正弦激励下电路的稳态响应 2.什么是正弦量? i(t)=Im cos(wt +j) u(t)=U cos(wt +j) 振幅角频率初相 ☆注意:本课程中所有正弦量均指余弦形式! 3.振幅与有效值之间关系 1==0.7071m,U= U m=0.707Um 2 2
知识点回顾 1. 本章研究对象? 2. 什么是正弦量? 正弦激励下电路的稳态响应 cos( ) ( ) cos( ) ( ) m i u m t u i t U t t I w w j j + = + = 振幅 角频率 初相 ☆注意:本课程中所有正弦量均指余弦形式! 0.707 , 0.707 2 2 m m m m I I U = = = = I U U 3. 振幅与有效值之间关系

知识点回顾 4.相位与相位差及其取值范围? i(t)=I cos(wt +j) u(t)=U cos(wt +j) 相位差:q=j4-j: 取值范围:1j,I,1j41,|9Ep 5.两正弦量同相、反相、正交的含义? 9=0,同相,g=p反相,9=号正交 6.两正弦量间如何进行运算? 传统方法:三角函数的各类运算 简便方法:相量法! 上节课还没讲到©
知识点回顾 4. 相位与相位差及其取值范围? ( ) cos( ) ( ) cos( ) m i m u i t I t u t U t w w j j = + = + u i 相位差:q = j j - | | |, ,| | | i u 取值范围:j j q p £ 0 2 p q q p q = = = ,同相, ,反相, ,正交 5.两正弦量同相、反相、正交的含义? 6.两正弦量间如何进行运算? 简便方法:相量法! 上节课还没讲到☺ 传统方法:三角函数的各类运算
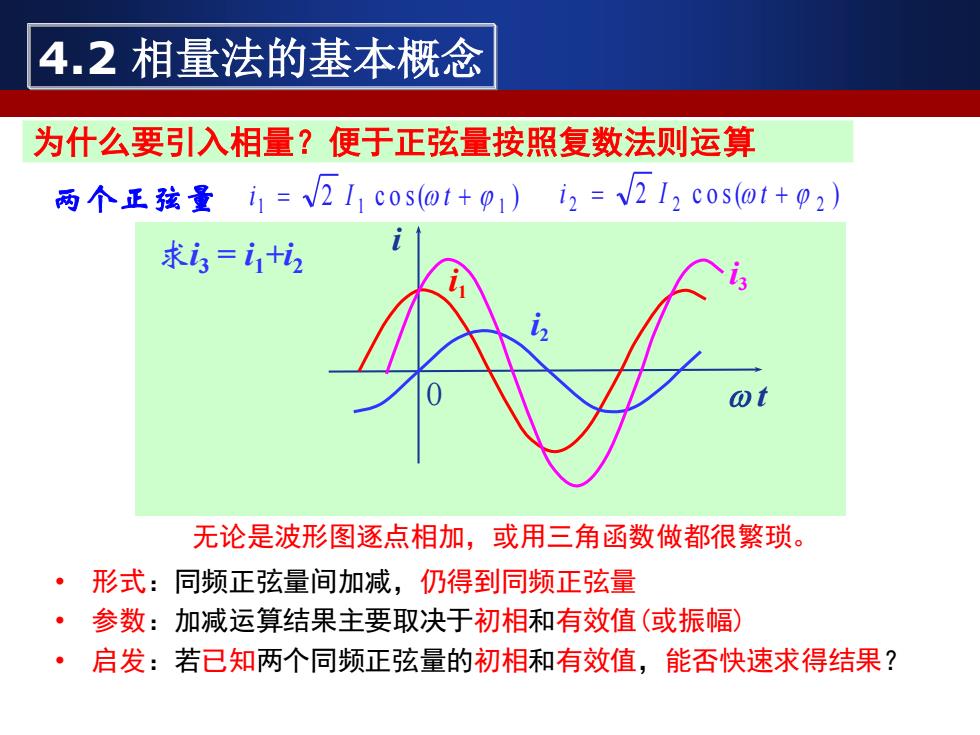
4.2相量法的基本概念 为什么要引入相量?便于正弦量按照复数法则运算 两个正孩量i1=V211c0sot+01)i2=V212c0s(o1+p2)》 求3=1+坊 无论是波形图逐点相加,或用三角函数做都很繁琐。 ·形式:同频正弦量间加减,仍得到同频正弦量 ·参数:加减运算结果主要取决于初相和有效值(或振幅) ·启发:若已知两个同频正弦量的初相和有效值,能否快速求得结果?
为什么要引入相量?便于正弦量按照复数法则运算 两个正弦量 i1+i2 →i3 w w w I1 I2 I3 1 2 3 无论是波形图逐点相加,或用三角函数做都很繁琐。 • 形式:同频正弦量间加减,仍得到同频正弦量 • 参数:加减运算结果主要取决于初相和有效值(或振幅) • 启发:若已知两个同频正弦量的初相和有效值,能否快速求得结果? 角频率: 有效值: 初相位: 2 c o s ( ) 1 1 w 1 i = I t + 2 c o s ( ) 2 2 w 2 i = I t + i1 i2 w t i i1 i2 0 i3 求i3 = i1+i2 4.2 相量法的基本概念

4.2相量法的基本概念 正弦量与相量 1、正弦量的相量表示 构造一个复函数A()=√21eo+o) =√21cos(o1+p)+jW2si(ot+p)】 若对A(t)取实部:Re[A(t)]=√21cos@t+p)是一个正弦量 对于任意一个正弦量都可以找到唯一的与其对应的复指数函数: i(t)=√2Icos(wt+j)?A(t) Vte) jp。jot 4A(0还可以写成 A(t)=√2Iee 复常数→&-lei=I?j )的相量形式 A()包含了三要素:、φ、o 复常数包含了I,p
1、正弦量的相量表示 构造一个复函数 j ( ) ( ) 2 e w + = t A t I 若对A(t)取实部: Re[A(t)]= 2Icos(w t + ) 是一个正弦量 对于任意一个正弦量都可以找到唯一的与其对应的复指数函数: A(t)包含了三要素:I、 、w 复常数包含了I , 。 A(t)还可以写成 t A t I jw ( ) 2 e e j = 复常数 = 2 Ic o s (w t + ) + j 2 Is in (w t + ) 4.2 相量法的基本概念 一、正弦量与相量 j I I I e j &= = ? j i(t)的相量形式 ( ) j( ) 2 cos( ) ( ) 2 t i t t A t e I I w j w j + = + ?

4.2相量法的基本概念 正弦量与相量 it)=V21c0s(0t+0,)←→1=1∠0, 相量的模表示正弦量的有效值 正弦量对应相量的含义 相量的幅角表示正弦量的初相 相量是一个特殊的复数,它能表征一个正弦量。复数的一切运算 均适用于相量。 正弦电压与相量的对应关系: ut)=√2cos(wM+j.) =U?j 振幅相量: u(t)=U cos(wt+j)p=U?j 相量图(相量画在复平面上) i(t)=Im cos(wt+j)p=Im?j 相量与振幅相量的关系是: =V2是=√8
相量是一个特殊的复数,它能表征一个正弦量。复数的一切运算 均适用于相量。 ( ) 2 c o s( ) i i i t = I w t + → I = I • 正弦量对应相量的含义 相量的模表示正弦量的有效值 相量的幅角表示正弦量的初相 正弦电压与相量的对应关系: 相量与振幅相量的关系是: 相量图(相量画在复平面上) 4.2 相量法的基本概念 一、正弦量与相量 u U& ( ) 2 cos( ) U u u u t wt j U& U j 振幅相量: ( ) cos( ) ( ) cos( ) m m m m u m u m u i u U U i I U I I t t t t j w j j w j = + = ? = = Þ + ? Þ & & 2 , 2 U I & m m = U I & & = &

4.2相量法的基本概念 正弦量与相量 例1.已知 i=100W2c0s314t+30°)A 解:i=100∠30°A u=220W2c0s(314t-60°)V j=220∠-60°V 试用相量表示i,u。 例2. 解: 己知1=50∠15°A,f=50Hz.i=50W2c0s(314t+15°)A 试写出电流的瞬时值表达式
例1.已知 试用相量表示 i , u 。 22 0 2 co s(3 1 4 t 6 0 ) V 100 2 co s(314 3 0 )A o o = − = + u i t 解: 220 6 0 V 100 3 0 A o o = − = • • U I 例2. 试写出电流的瞬时值表达式。 解: 5 0 2 c o s (314 1 5 ) A 5 0 1 5 A , 5 0 H z . i = t + = = • I f 已 知 4.2 相量法的基本概念 一、正弦量与相量
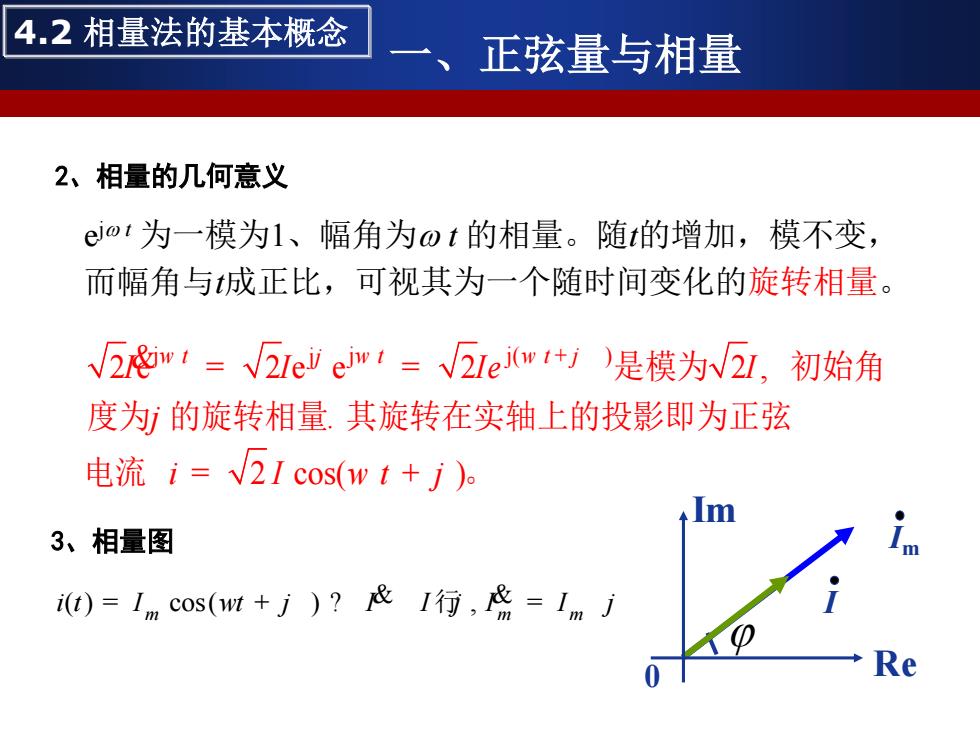
4.2相量法的基本概念 正弦量与相量 2、相量的几何意义 eot为一模为1、幅角为ot的相量。随t的增加,模不变, 而幅角与成正比,可视其为一个随时间变化的旋转相量。 √2w1=√2leew1=√2 lej(w/)是模为N2L,初始角 度为ⅵ的旋转相量.其旋转在实轴上的投影即为正弦 电流i=√2Icos(wt+j)。 3、相量图 m i)=1mcos(M+j)?&I行,&=1mj Re
2、相量的几何意义 e jw t 为一模为1、幅角为w t 的相量。随t的增加,模不变, 而幅角与t成正比,可视其为一个随时间变化的旋转相量。 j j j( ) j 2 e 2 e e 2 2 , . 2 cos( ) t t t I I Ie I i I t w w w j j j w j + = = = + & 是模为 初始角 度为 的旋转相量 其旋转在实轴上的投影即为正弦 电流 。 4.2 相量法的基本概念 一、正弦量与相量 3、相量图 ( ) cos( ) , m m m i t I t I = + = w j j j ? I I & & I行 Im Re 0 Im I

4.2相量法的基本概念 二、 正弦量的相量运算 1、同频率正弦量相加减 u(t)=2Ucos(@t+)=Re(v2Uei') u2(t)=√2U2cos(ot+p2)=Re(√2j2eJo') 复数运算u()=4,()+u,()=Re(V2j1eo)+Re(√2jeo) Re=Re()=Re(v2+U2)ei) 可得其相量关条为:0=U,+U, 相量运算 W1±W2=3 将三角函数运算转化为相量运算 运算法则:与复数相同! &?咚 (1)直角坐标实部虚部加减 (2)极坐标相量图平行四边形法则
1、 同频率正弦量相加减 将三角函数运算转化为相量运算 运算法则:与复数相同! (1)直角坐标实部虚部加减 (2)极坐标相量图平行四边形法则 ( ) 2 cos( ) R e( 2 e ) ( ) 2 cos( ) R e( 2 e ) j 2 2 2 2 j 1 1 1 1 t t u t U t U u t U t U w w w w • • = + = = + = R e( 2 e 2 e ) R e( 2 ( ) e ) ( ) ( ) ( ) R e( 2 e ) R e( 2 e ) j 1 2 j 2 j 1 j 2 j 1 1 2 t t t t t U U U U u t u t u t U U w w w w w • • • • • • = + = + = + = + U U U 1 U 2 可得其相量关系为: = + u1 u2 = u3 U U U 1 2 3 & & & ? Re[ 2 e ] j t U& w 4.2 相量法的基本概念 二、正弦量的相量运算 复数运算 相量运算
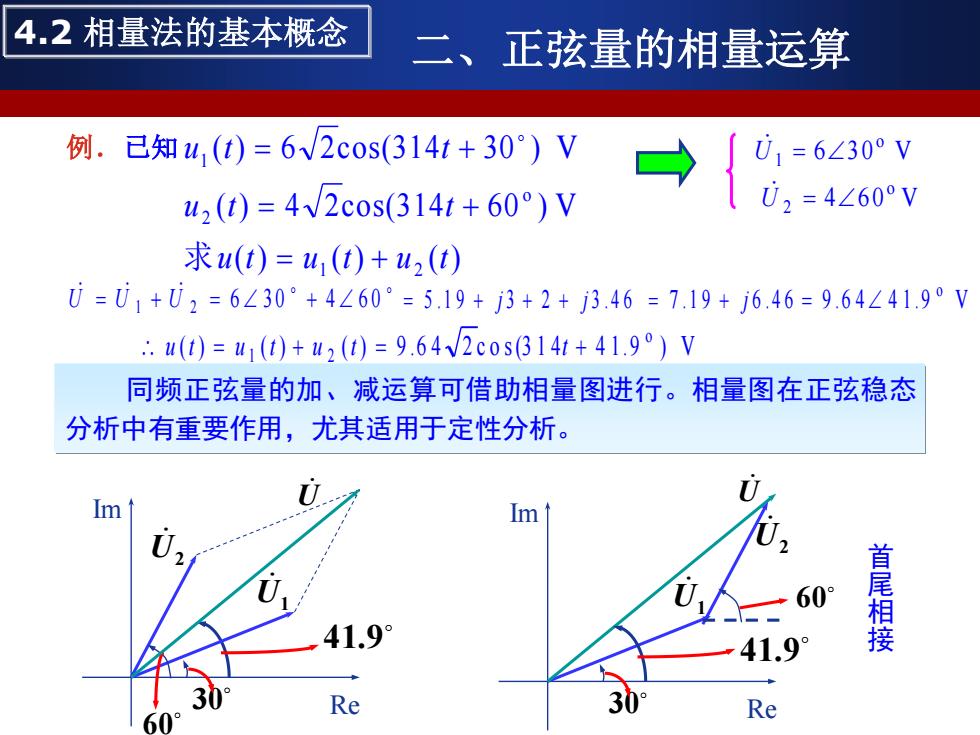
4.2相量法的基本概念 正弦量的相量运算 例. 己知u,(t)=6V2cos(314t+30)V U =6∠30°V u2(t)=4W2c0s(3141+60)V U2=4∠60°V 求(t)=u,(t)+u2(t) 0=U1+U2=6L30°+4∠60°=5.19+j3+2+j3.46=7.19+j6.46=9.64L41.9°V ∴u(t)=41(t)+u2(t)=9.64V2c0s314t+41.9°)V 同频正弦量的加、减运算可借助相量图进行。相量图在正弦稳态 分析中有重要作用,尤其适用于定性分析。 Im 60° 41.9° 首尾相接 41.9 Re Re
例.已知 ( ) ( ) ( ) ( ) 4 2cos(314 6 0 ) V ( ) 6 2cos(314 3 0 ) V 1 2 o 2 1 u t u t u t u t t u t t = + = + = + 求 同频正弦量的加、减运算可借助相量图进行。相量图在正弦稳态 分析中有重要作用,尤其适用于定性分析。 4 6 0 V 6 3 0 V o 2 o 1 = = U U ( ) ( ) ( ) 9 .6 4 2 c o s (314 4 1 .9 ) V o 1 2 u t = u t + u t = t + 6 3 0 4 6 0 U = U 1 + U 2 = + Re Im 30 U1 41.9 U Re Im 41.9 30 U1 60U2 U 首 尾 相 接 = 5 . 1 9 + j 3 + 2 + j 3 . 4 6 = 7 .1 9 + j 6 .4 6 9 .6 4 4 1 .9 V o = 60 U2 4.2 相量法的基本概念 二、正弦量的相量运算

4.2相量法的基本概念 二、正弦量的相量运算 2、正弦量的微分、积分运算 i=√21cos(0t+0;)分i=1Lp 微分运算: 积分运算: di ka1coso+ di= ∫idt=∫21coso1+p,)d =√2Lsin(ot+o,) =-√2Isin(ot+p;)o =V201cos(o1+p,+2) -2 cos(@1+;-) 相量形式 相量形式 di w1e0,+ òidh? 1.0 -e 2 时域微分: di(t dt 时域积分: [i(t)dt←→ 10
2、正弦量的微分、积分运算 2 c o s ( ) i i i = I w t + I = I ) 2 2 cos( 2 sin( ) 2 cos( ) w w w w w = + + = − + = + i i i I t I t I t d t d d t d i ) 2 ( ( ) d 2 cos( ) d cos 2 2 sin w w w = + − = + = + i i i t t i t I t t ω I ω I { ( ) 2 2 i i j j j di j I j I dt Ie e e p j j p w w w + ? = & { ( ) 2 2 e e e i i j j j j I i d j I t I p p j j w w w - ò ? = & 微分运算: 积分运算: j I d t d i t → w ( ) 时域微分: 时域积分: → jw I i t d t ( ) 4.2 相量法的基本概念 二、正弦量的相量运算 相量形式 相量形式