
第五章原子结构 本章知识点与考核要求 •核外电子的运动的特殊性 •核外电子运动状态的描述 •多电子原子结构 •元素周期表 •元素性质的周期性
第五章 原子结构 本章知识点与考核要求 •核外电子的运动的特殊性 •核外电子运动状态的描述 •多电子原子结构 •元素周期表 •元素性质的周期性

第一节, 核外电子的特殊性 原子是化学变化中的最小微粒。 一波尔理论 氢原子是最简单、最理想的原子。 将低压氢气的放电管发出的光通过分光棱 镜可以得到四条明显的光谱线
第一节 核外电子的特殊性 一 .波尔理论 氢原子是最简单、最理想的原子。 将低压氢气的放电管发出的光通过分光棱 镜可以得到四条明显的光谱线。 原子是化学变化中的最小微粒
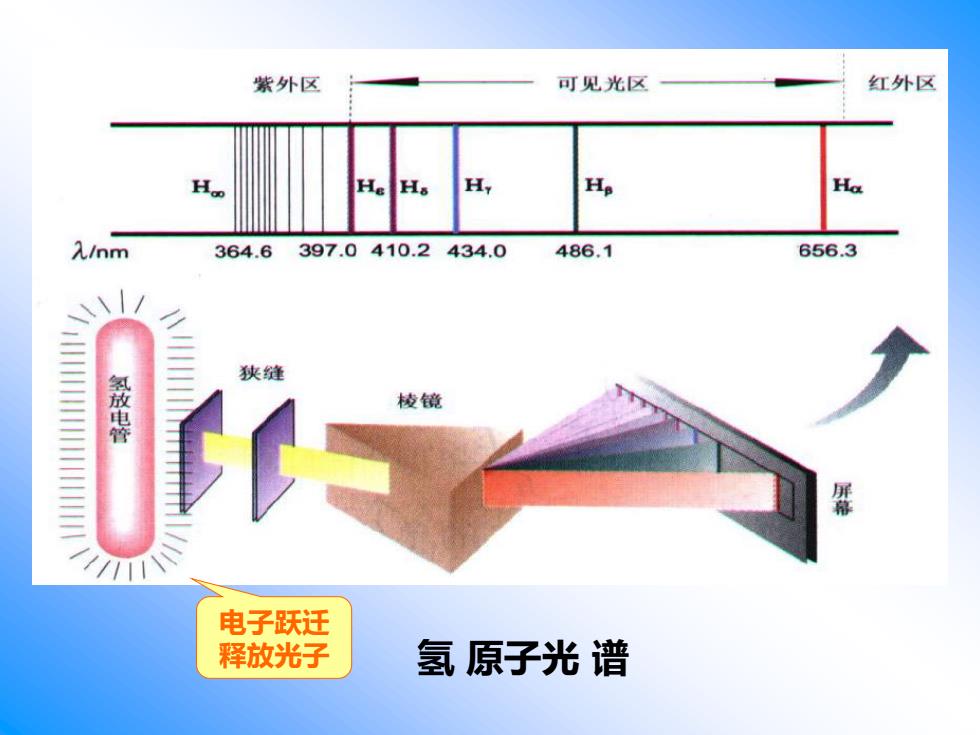
紫外区 可见光区 红外区 Ha H 入/nm 364.6 397.0410.2434.0 486.1 656.3 狭缝 氢放电管 棱镜 电子跃迁 释放光子 氢原子光谱
氢 原子光 谱 电子跃迁 释放光子

1913年,丹麦Bohr的“定态原子模型”(波尔理 论借助Planck的热辐射的量子理论、Einstein的光 子学说、Rutherford的行星式原子模型,建立了 氢原子模型。提出了著名的Bohr理论。 1.电子沿固定轨道绕核运动,电子在轨道上运动 时,不吸收也不辐射能量,称为“定态”;在一定的 轨道上运动的电子具有一定的能量值E称为能级。 能量最低时,称为基态(ground state)。 电子能量较高,称为激发态(excited state)
1913年,丹麦Bohr的“定态原子模型” (波尔理 论)借助Planck的热辐射的量子理论、Einstein的光 子学说、 Rutherford 的行星式原子模型,建立了 氢原子模型。提出了著名的Bohr理论。 1. 电子沿固定轨道绕核运动,电子在轨道上运动 时,不吸收也不辐射能量,称为“定态” ;在一定的 轨道上运动的电子具有一定的能量值E,称为能级。 能量最低时,称为基态(ground state)。 电子能量较高,称为激发态(excited state)

2能级间的跃迁:当电子能量由一个能级改变为另一 个能级时,称为跃迁(transition)。电子跃迁时所 吸收或辐射的光子的能量等于两能级差,即: hw=E2-E1=△E U为光子的频率; 为普朗克常数(6.626×10-34Js) ·Bohr成功地解释了氢原子的稳定性和不连续光谱。 但未能冲破经典物理学的束缚,不能解释多电子原 子光谱,甚至不能说明氢原子光谱的精细结构。 微观粒子的运动不遵守经典物理学规律,具有波粒二象性
2.能级间的跃迁:当电子能量由一个能级改变为另一 个能级时,称为跃迁(transition)。电子跃迁时所 吸收或辐射的光子的能量等于两能级差,即: υ 为光子的频率; h为普朗克常数(6.626×10-34 J·s) hυ = E2-E1 =△E •Bohr成功地解释了氢原子的稳定性和不连续光谱。 但未能冲破经典物理学的束缚,不能解释多电子原 子光谱,甚至不能说明氢原子光谱的精细结构。 微观粒子的运动不遵守经典物理学规律,具有波粒二象性

二、电子的波粒二象性(Duality) 1924年法国物理学家德布罗意 (L.de Brogile)在研究电子的运动 规律时,受光的波粒二象性的启发 大胆提出: 电子等实物粒子(原子、质子、中子) 不仅具有粒子性,也具有波动性。 德布罗意,L. 电子绕核运动具有波粒二象性(特殊性)。既有微 粒性(具有质量和速度),又有波动性(有波长)
二、电子的波粒二象性(Duality) 1924年法国物理学家德布罗意 (L.de Brogile) 在研究电子的运动 规律时,受光的波粒二象性的启发, 大胆提出: 电子等实物粒子(原子、质子、中子) 不仅具有粒子性,也具有波动性。 电子绕核运动具有波粒二象性(特殊性)。既有微 粒性(具有质量和速度),又有波动性(有波长)

1927年,美国的Davisson和Germeri证明了 电子束同X射线一样具有波动性。如下图: 晶体 晶体 电子源 a 电子源 (b) (c) 行射强度大的地方出现的机会多 衍射强度小的地方出现的机会少
衍射强度大的地方出现的机会多, 衍射强度小的地方出现的机会少. 1927年,美国的Davisson和Germer证明了 电子束同X射线一样具有波动性。如下图:

第二节核外电子运动状态的描述 一、波函数 电子具有波粒二象性。它是在 原子核静电引力作用下的运动 这种运动如何去描述呢? 1926年奥地利物理学家 Schrodinger提出了著名的薛 定鄂方程,它是在力场作用下 薛定谔,E 微观粒子运动的波动方程。 6为ap+Cp+8πm(B-p帅=0 h
第二节 核外电子运动状态的描述 1926年奥地利物理学家 Schrödinger提出了著名的薛 定鄂方程,它是在力场作用下 微观粒子运动的波动方程。 电子具有波粒二象性。它是在 原子核静电引力作用下的运动, 这种运动如何去描述呢? 一、波函数 ( ) 0 8 2 2 2 2 2 2 2 2 + + + − = E V m x y z h

(1)波函数是Schrodinger方程的解,它不是一个数 值,而是一个空间坐标的函数式。 (2)电子的运动状态用波函数描述。波函数表 示电子的概率密度。 (3)描述原子中单个电子运动状态的波函数少称为 原子轨道(atomic orbital)。原子轨道的大小指电 子出现的概率在99%的空间区域的界面。 (4)解Schrodinger方程可以获得一系列合理的解少 及其相应的能量E,电子的能量是不连续的(量子化)
(1)波函数Ψ是Schrodinger方程的解,它不是一个数 值,而是一个空间坐标的函数式。 (3)描述原子中单个电子运动状态的波函数Ψ 称为 原子轨道(atomic orbital)。原子轨道的大小指电 子出现的概率在99%的空间区域的界面。 (4) 解Schrodinger方程可以获得一系列合理的解Ψ 及其相应的能量E ,电子的能量是不连续的(量子化)。 (2)电子的运动状态用波函数ψ描述。波函数ψ2表 示电子的概率密度

薛定鄂方程有很多解,但并非每个解都合理。 要取得合理解,需引入三个参数八、人m,称为量 子数,当三个量子数的取值和组合一定时,就有了一个 确定的波函数n.1.m(G8p) 三个量子数的取值限制和物理意义 1.主量子数(principal quantum number) n n=1,2,3.非零的任意正整数 n又称为电子层(shell) 光谱学上:K、L、M、N、O、P、Q. 物理意义:决定电子在核外空间出现概率最大的区域 离核的远近;决定电子能量高低的主要因素
薛定鄂方程有很多解,但并非每个解都合理。 要取得合理解,需引入三个参数 n、l、m,称为量 子数, 当三个量子数的取值和组合一定时,就有了一个 确定的波函数Ψn、l、m(r,θ,φ) 。 1. 主量子数 (principal quantum number) n 物理意义:决定电子在核外空间出现概率最大的区域 离核的远近;决定电子能量高低的主要因素。 n = 1, 2, 3. 非零的任意正整数 n又称为电子层( shell ) 光谱学上:K、L、 M、N、O、P、Q. 三个量子数的取值限制和物理意义: