
For most systems,we can use(spin-polarized)PBE functional; For systems with d-and f-orbitals,we may use DFT+U, depending on the properties we study; Strategy for For systems with small formation/adsorption/...energies(<-50 meV),we may consider DFT+vdW; true ab-initio For semiconductors,compare the structure,electronic states modelling and band gap values with possible experiments,then decide the adopted functional; May apply HSE functional only at some critical steps because of its poor efficiency; Perform GW on top of the HSE functional,if needed. Based on things you want to know!
Strategy for true ab-initio modelling For most systems, we can use (spin-polarized) PBE functional; For systems with d- and f- orbitals, we may use DFT+U, depending on the properties we study; For systems with small formation/adsorption/… energies (<~50 meV), we may consider DFT+vdW; For semiconductors, compare the structure, electronic states and band gap values with possible experiments, then decide the adopted functional; May apply HSE functional only at some critical steps because of its poor efficiency; Perform GW on top of the HSE functional, if needed. Based on things you want to know!

Beyond GGA-DRT+U The L(S)DA/GGA often fails to describe systems with localized(strongly correlated)d andf electrons >wrong one-electron energies Strong intra-atomic interaction is introduced in a(screened)Hartree-Fock like manner,as an on site replacement of the L(S)DA/GGA>the L(S)DA+U method. Dudarev's approach to DFT+U The DFT+U Hamitonian includes contributions already accounted for in the DFT functional> subtract double-counting,adopt rotationally invariant formulation. This can be understood as adding a penalty functional to the DFT total energy expression that forces the on site occupancy matrix in the direction of idempotency. The on site Coulomb-parameter,U=E(dn+)+E(dn-1)-2E(dn),and exchange parameter J. The U and J parameters do not enter separately,only the difference (UJ)is meaningful
Beyond GGA – DFT + U • The L(S)DA/GGA often fails to describe systems with localized (strongly correlated) d and f electrons → wrong one-electron energies • Strong intra-atomic interaction is introduced in a (screened) Hartree-Fock like manner, as an on site replacement of the L(S)DA/GGA → the L(S)DA+U method. Dudarev’s approach to DFT+U ✓ The DFT+U Hamitonian includes contributions already accounted for in the DFT functional → subtract double-counting, adopt rotationally invariant formulation. ✓ This can be understood as adding a penalty functional to the DFT total energy expression that forces the on site occupancy matrix in the direction of idempotency. ✓ The on site Coulomb- parameter, U = E(dn+1) + E(dn-1 ) – 2E(d n ), and exchange parameter J. ✓ The U and J parameters do not enter separately, only the difference (U −J) is meaningful
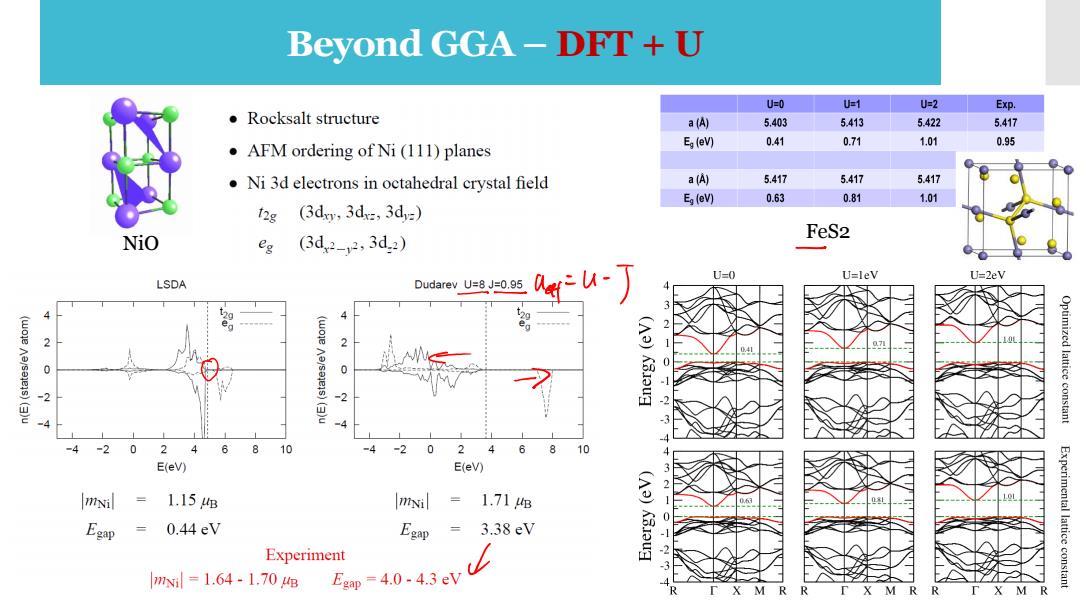
Beyond GGA-DRT+U U=0 U=1 U=2 Exp. ●Rocksalt structure a(A) 5.403 5.413 5.422 5.417 Eg(eV) 0.41 0.71 1.01 0.95 AFM ordering of Ni(111)planes Ni 3d electrons in octahedral crystal field a() 5.417 5.417 5.417 Eg(eV) 0.63 0.81 1.01 12g (3dxy,3dx,3d=) NiO FeS2 eg (3d2-2,3d2) fu-丁 U=0 U=leV U=2eV LSDA Dudarev U=8 J=0.95 2 2 7 0 0 ()u 2 Optimized lattice constant -2 0 24 6 8 10 4 -2 0 24 6 8 10 E(eV) E(eV) mNil 1.15B mNi = 1.71g Egap 0.44eV Egap = 3.38eV (A3)K3oug Experiment -2 Experimental lattice constant 3 mx=1.64-1.70e Egp=4.0.4.3eV M R
Beyond GGA – DFT + U NiO FeS2

Beyond GGA--GGA+vdW Popular local and semilocal density functionals are unable to describe correctly van der Waals interactions resulting from dynamical correlations between fluctuating charge distributions. EDFT-disp =EKS-DFT+Edisp:Edisp=- 1 Nar Na Add vdW correction to potential energy,interatomic forces,as well as stress tensor and hence simulations such as atomic and lattice relaxations,molecular dynamics,and vibrational analysis Nat (via finite differences)can be performed. Edisp = DFT-D2 by Grimme et al. S.Grimme.,J.Comp.Chem.27,1787(2006). DFT-D3 by Grimme et al. S.Grimme,J.Antony,S.Ehrlich,and S.Krieg,J.Chem.Phys.132,154104(2010) A.Tkatchenko,R.A.Di Stasio,R.Car,and M.Scheffler,Phys.Rev.Lett.108,236402(2012) DFT-TS by Tkatchenko-Scheffler M.Dion,H.Rydberg,E.Schr"oder,D.C.Langreth,and B.I.Lundqvist,Phys.Rev.Lett.92, vdW-DF and by Langreth and 246401(2004) Lundqvist et al.(PBE) K.Lee,E.D.Murray,L.Kong,B.I.Lundqvist,and D.C.Langreth,Phys.Rev.B82,081101 (2010)
Popular local and semilocal density functionals are unable to describe correctly van der Waals interactions resulting from dynamical correlations between fluctuating charge distributions. • Add vdW correction to potential energy, interatomic forces, as well as stress tensor and hence simulations such as atomic and lattice relaxations, molecular dynamics, and vibrational analysis (via finite differences) can be performed. Beyond GGA -- GGA + vdW DFT-D2 by Grimme et al. DFT-D3 by Grimme et al. DFT-TS by Tkatchenko-Scheffler vdW-DF and by Langreth and Lundqvist et al. (PBE) S. Grimme., J. Comp. Chem. 27, 1787 (2006). S. Grimme, J. Antony, S. Ehrlich, and S. Krieg, J. Chem. Phys. 132, 154104 (2010) A. Tkatchenko, R. A. Di Stasio, R. Car, and M. Scheffler, Phys. Rev. Lett. 108, 236402 (2012) M. Dion, H. Rydberg, E. Schr ¨oder, D. C. Langreth, and B. I. Lundqvist, Phys. Rev. Lett. 92, 246401 (2004) K. Lee, E. D. Murray, L. Kong, B. I. Lundqvist, and D. C. Langreth, Phys. Rev. B 82, 081101 (2010)
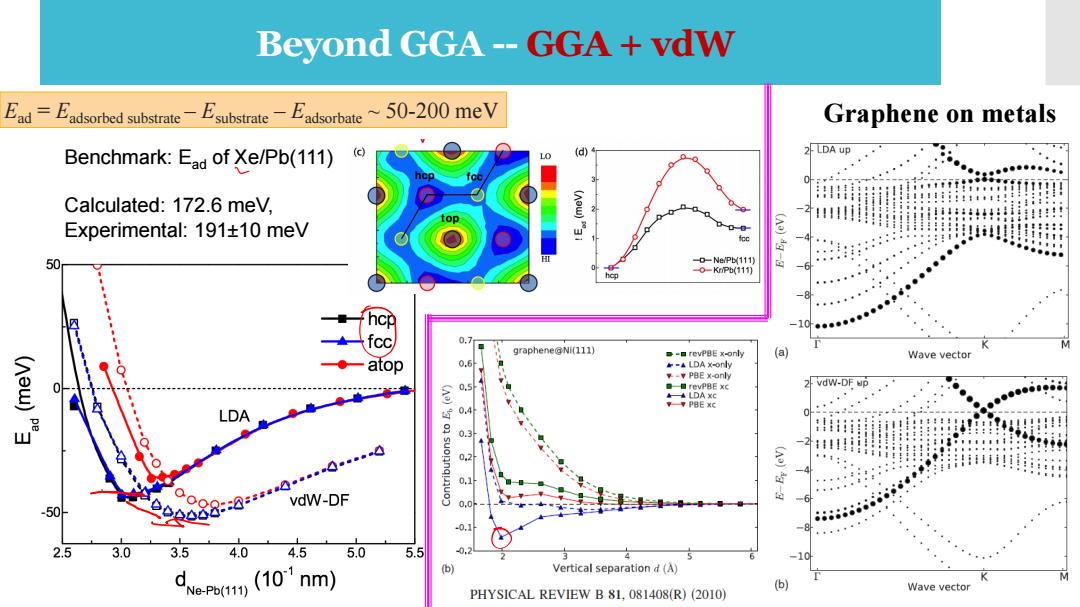
Beyond GGA--GGA+vdW Ead-Fadsorbed substrateEsubstrate Eadsorbate~50-200 meV Graphene on metals Benchmark:Ead of Xe/Pb(111) (c) 2 LDA up L Calculated:172.6 mev, 进 ::11111 !目!目日:1:.1 Experimental:191+10 meV -D-Ne/Pb(111) 0-KP(11) 6 hcp : +一fcc 0.7 graphene@Ni(111) e-口revPBE x-only Wave vector atop -LDA xonly PBE x-only 0,5 revPBE xc 2 vdw-DF up LDA LDA 0.q Hiii用 -11 0.1 vdW-DF 6 -50 0888:0-590☑ 0,0 568686666888445 0, 2.5 3.0 3.5 4.0 4.5 5.0 5.5 0. -10 (10'nm) (b) Vertical separation d(A) 6 M Ne-Pb(111) Wave vector PHYSICAL REVIEW B 81,081408(R)(2010)
Beyond GGA -- GGA + vdW Benchmark: Ead of Xe/Pb(111) Calculated: 172.6 meV, Experimental: 191±10 meV Ead = Eadsorbed substrate – Esubstrate – Eadsorbate ~ 50-200 meV Graphene on metals

Beyond GGA--GW approximation Calculate DFT/hybrid functional wavefunctions A+Vion(r)+ve(r)+vx(r) p(r)=En(r) 2m Determine Green function and W using DFT wavefunctions Determine first order change of energies h" 21 △+Vom+V+∑(GW)p)=En Update Green's function and self-energy(W fixed to W) Gr,r)=∑ (r)0(r) 0-E-E +i sgnl En EFomi M.S.Hybertsen,S.G.Louie,Phys.Rev.B 34,5390(1986)
Beyond GGA -- GW0 approximation Calculate DFT/hybrid functional wavefunctions Determine Green function and W using DFT wavefunctions Determine first order change of energies Update Green’s function and self-energy (W fixed to W0 ) M. S. Hybertsen, S. G. Louie, Phys. Rev. B 34, 5390 (1986) ( ) ( ) ( ) ( ) ( ) 2 2 r r r r r n n n e V V V E m = − + + + ion e l xc n n e n V V GW E m − + + +( ) = 2 0 2 ion e l − − + − = m m m Fermi m m E E i E E G sgn[ ] ( ) ( ) ( , ) r r r r

The Accuracy of DFT ·Atomic structures bond lengths and lattice constants are accurate to within 1-2% ·Energies several meVs;but depends on different functionals Vibrational frequencies within 5-10%accuracy
Atomic structures bond lengths and lattice constants are accurate to within 1-2% Energies several meVs; but depends on different functionals Vibrational frequencies within 5-10% accuracy The Accuracy of DFT

The limitations of DFT ·Band-gap problem HKS theorem is not valid for excited states; band-gaps in semiconductors and insulators are usually underestimated. ·Overbinding -LSDA:too small lattice constants,too large cohesive energies,too high bulk moduli; -The use of the GGA is mandatory for calculating adsorption energies,but the choice of the "correct"GGA is important. Neglect of strong correlations -Exchange-splitting underestimated for narrow d-and f-bands; Many transition-metal compounds are charge-transfer insulators,but DFT predicts metallic state. Neglect of van der Waals interactions -vdW forces are not included in any DFT functional; -Approximate expression of vdW forces on the basis of local polarizabilities derived from DFT
The limitations of DFT Band-gap problem - HKS theorem is not valid for excited states; - band-gaps in semiconductors and insulators are usually underestimated. Overbinding - LSDA: too small lattice constants, too large cohesive energies, too high bulk moduli; - The use of the GGA is mandatory for calculating adsorption energies, but the choice of the “correct” GGA is important. Neglect of strong correlations - Exchange-splitting underestimated for narrow d- and f-bands; - Many transition-metal compounds are charge-transfer insulators, but DFT predicts metallic state. Neglect of van der Waals interactions - vdW forces are not included in any DFT functional; - Approximate expression of vdW forces on the basis of local polarizabilities derived from DFT
Building models Cubo-Oh:M@Pt12 ody-centered cublc Face-centered cublc (b) Dual Catalytic Site side view La SroMnO, BaTiO, La SreMnO, 42

Crystal Structures Bravais Lattice:specifies the periodic array in which the repeated units of the crystal are arranged. The unit themselves may be single atoms,groups of atoms,molecules,and ions. R=na+naz+ngas a,a,as:primitive vectors The position of the center of an atom i of the basis relative to the associated lattice point is An ideal crystal is constructed by the t,=x1a1+x2ā2+X,ā3 infinite repetition of identical structure where0≤x,x2,x3≤1 units in space
Crystal Structures An ideal crystal is constructed by the infinite repetition of identical structure units in space. Bravais Lattice: specifies the periodic array in which the repeated units of the crystal are arranged. The unit themselves may be single atoms, groups of atoms, molecules, and ions. The position of the center of an atom i of the basis relative to the associated lattice point is