材料与能源学院 School of Materials and Energy 《材料分子结构分析》 第六章拉曼光谱 Raman spectroscopy wvalp on moy 1abiofianau 刘钰 电子科技大学 激光 Raman散射 2021年2022年春季 样品
第六章 拉曼光谱 刘 钰 电子科技大学 2021年-2022年 春季 Raman spectroscopy 《材料分子结构分析》

never forget how to dream 目录 6.1 拉曼光谱概述 6.2 拉曼光谱的基本原理 6.3 拉曼光谱的表示方法 6.4拉曼光谱与红外光谱的比较 6.5拉曼光谱的特征谱带 6.6拉曼光谱的优越性 6.7拉曼光谱仪 6.8样品的准备 6.9拉曼光谱的常规分析方法 6,10拉曼光增的应用 I 2
2 目录 6.1 拉曼光谱概述 6.2 拉曼光谱的基本原理 6.3 拉曼光谱的表示方法 6.4 拉曼光谱与红外光谱的比较 6.5 拉曼光谱的特征谱带 6.6 拉曼光谱的优越性 6.7 拉曼光谱仪 6.8 样品的准备 6.9 拉曼光谱的常规分析方法 6.10 拉曼光谱的应用

6.1拉曼光谱概述 never forget how to dream 1928年,印度科学家C.V.Raman首先 在CCl4的光谱中发现,当光与分子相互 作用后,一部分光的波长会发生变化( 颜色发生变化),通过对这些颜色发生 变化的散射光的研究,可以得到分子结 构的信息。这种效应就被命名为Raman 效应。 Sir C.V.Raman Nobel Prize 1930 RAHAN'S SPECTROGRAPH E FHBT BARAN BPECTRUN WAS 第一台观察Raman效应的装置 3
3 1928年,印度科学家 C.V. Raman 首先 在CCl4的光谱中发现,当光与分子相互 作用后,一部分光的波长会发生变化( 颜色发生变化),通过对这些颜色发生 变化的散射光的研究,可以得到分子结 构的信息。这种效应就被命名为Raman 效应。 第一台观察Raman效应的装置 Sir C.V. Raman Nobel Prize 1930 6.1 拉曼光谱概述

6.2拉曼光谱的基本原理 never forget how to dream principle of Raman spectroscopy 激发虚态 h(Vo-△v) E基态;E,振动激发态;E。+ hvo,E1+hvo激发虚态; 获得能量后,跃迁到激发虚态 ,Eo+hvo」 hvo hvo hvo hvo+△v 瑞利撒射 E, V=1 h△v scatter aser Eo V=0 Rayleigh散射 Raman散射 Rayleigh散射:弹性碰撞; 无能量交换,仅改变方向; laser 拉曼散射 Ramani散射:非弹性 碰撞;方向改变且有能 量交换; 4
4 6.2 拉曼光谱的基本原理 principle of Raman spectroscopy Raman散射: 非弹性 碰撞;方向改变且有能 量交换; Rayleigh散射:弹性碰撞; 无能量交换,仅改变方向; Rayleigh散射 Raman散射 h E0 E1 V=1 V=0 h0 h0 h0 h0 + E1 + h0 E0 + h0 h(0 - ) 激发虚态 E0基态;E1振动激发态; E0 + h0, E1 + h0 激发虚态; 获得能量后,跃迁到激发虚态
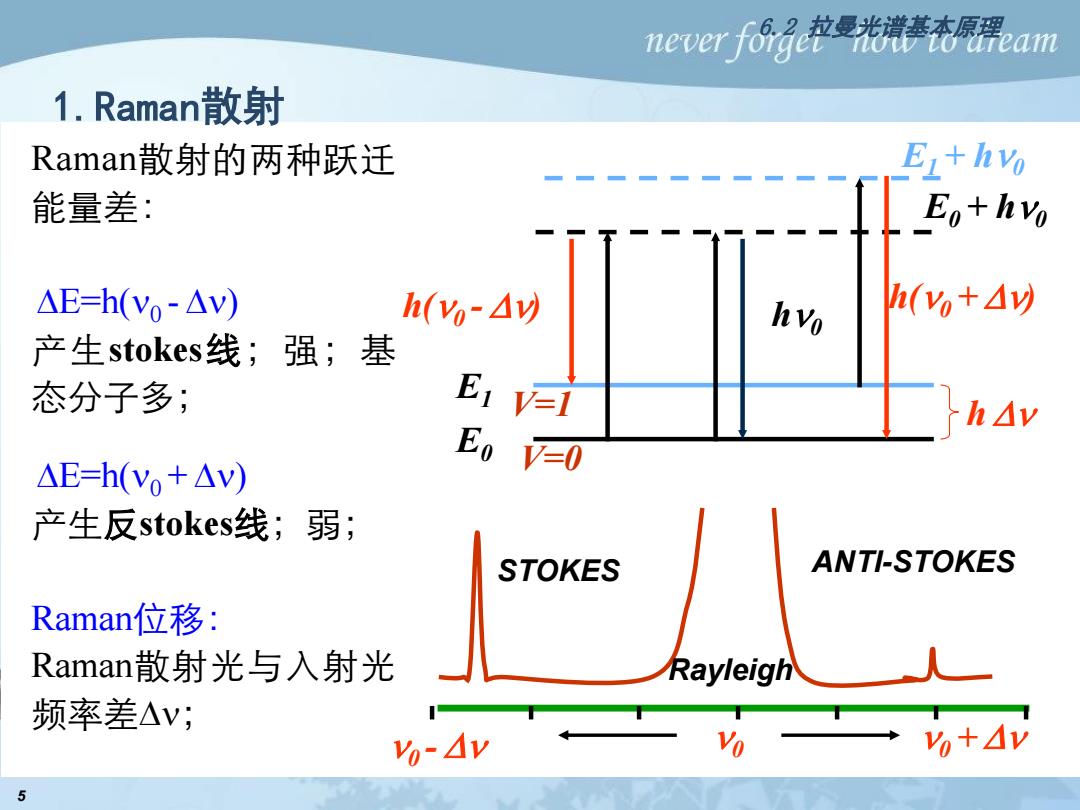
never fo拉曼光基在原隅am 1.Ramani散射 Raman散射的两种跃迁 E1+hvo 能量差: Eo+hvo △E=h(Vo~△v) h(y,-△) hvo h(y,+△y 产生stokes线;强;基 态分子多; E1=1 hAv Eo AE=h(Vo+△v) V=0 产生反stokes线;弱; STOKES ANTI-STOKES Raman位移: Raman散射光与入射光 Rayleigh 频率差△V; %-y Vo %+y 5
5 1.Raman散射 Raman散射的两种跃迁 能量差: E=h(0 - ) 产生stokes线;强;基 态分子多; E=h(0 + ) 产生反stokes线;弱; Raman位移: Raman散射光与入射光 频率差; ANTI-STOKES 0 - Rayleigh STOKES 0 0 + h(0 + ) E0 E1 V=1 V=0 E1 + h0 E0 + h0 h h0 h(0 - ) 6.2 拉曼光谱基本原理

never fo拉曼光灣基花愿理eam 光子将一部分能量传递给样品分子或从样品分子获得一部分 能量,从而改变了光的频率。能量变化所引起的散射光频率 变化称为拉曼位移 拉曼位移的计算 拉曼位移△V=(1I入入射一1I入散射)X107 如,用514.50nm激光激发氮气的拉曼散射波长为584.54nm, 对该拉曼峰以波数计的拉曼位移为: (1/514.50nm-1/584.54nm)×107=2329cm-1 6
6 拉曼位移的计算 拉曼位移 = (1/λ入射 – 1/λ散射)× 107 如,用514.50nm激光激发氮气的拉曼散射波长为584.54nm, 对该拉曼峰以波数计的拉曼位移为: (1/514.50nm – 1/584.54nm)× 107 = 2329 cm-1 6.2 拉曼光谱基本原理 光子将一部分能量传递给样品分子或从样品分子获得一部分 能量,从而改变了光的频率。能量变化所引起的散射光频率 变化称为拉曼位移

never f8拉曼花基原得am 2.产生拉曼位移的条件 对不同物质:△v不同; 对同一物质:△ν与入射光频率无关;表征分子振-转能级的 特征物理量;定性与结构分析的依据; 拉曼活性: ■对于分子振动和转动,拉曼活性是根据极化率 是否改变来判断。 光电场E中,分子极化率和分子产生诱导偶极距ρ的关系: p=aE 7
7 2. 产生拉曼位移的条件 对不同物质: 不同; 对同一物质: 与入射光频率无关;表征分子振-转能级的 特征物理量;定性与结构分析的依据; 光电场 E中, 分子极化率和分子产生诱导偶极距的关系: = E 拉曼活性: ◼ 对于分子振动和转动,拉曼活性是根据极化率 是否改变来判断。 6.2 拉曼光谱基本原理
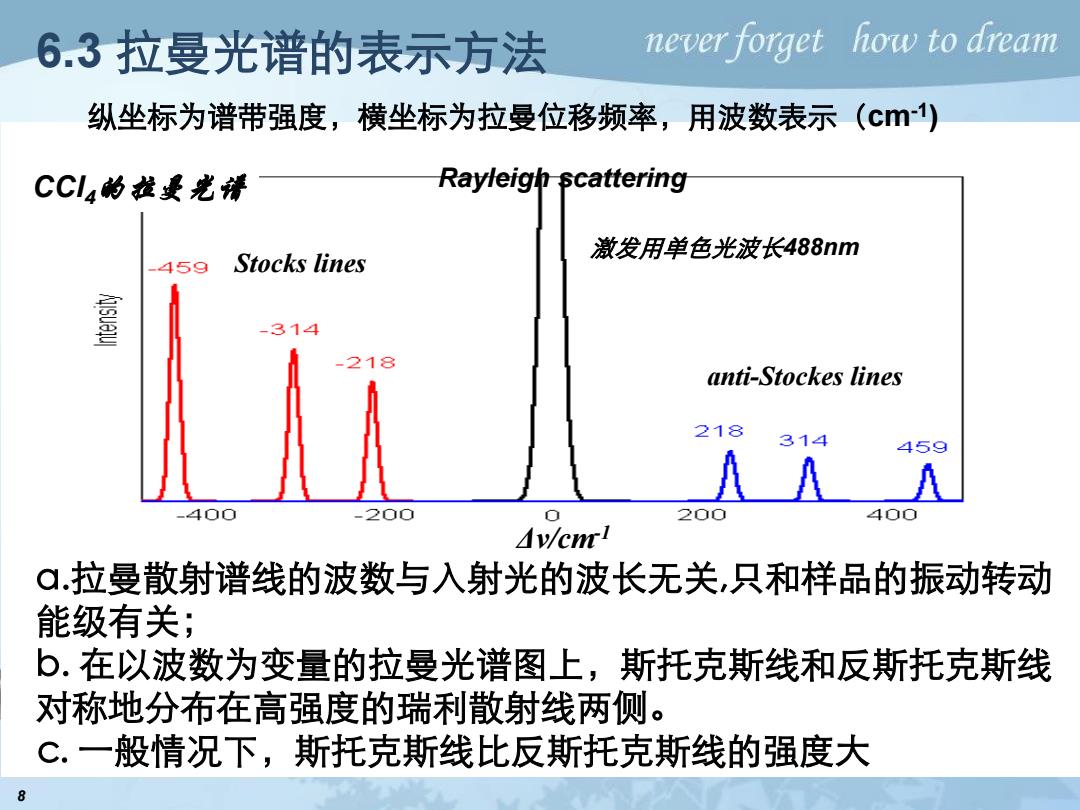
6.3拉曼光谱的表示方法 never forget how to dream 纵坐标为谱带强度,横坐标为拉曼位移频率,用波数表示(c) CCla的拉曼光清 Rayleigh scattering 激发用单色光波长488nm .459 Stocks lines 毫 -314 -218 anti-Stockes lines 218 314 459 -400 -200 0 200 400 Av/en ā.拉曼散射谱线的波数与入射光的波长无关,只和样品的振动转动 能级有关; b.在以波数为变量的拉曼光谱图上,斯托克斯线和反斯托克斯线 对称地分布在高强度的瑞利散射线两侧。 C.一般情况下,斯托克斯线比反斯托克斯线的强度大 8
8 CCl4的拉曼光谱 Stocks lines anti-Stockes lines Rayleigh scattering Δν/cm-1 6.3 拉曼光谱的表示方法 a.拉曼散射谱线的波数与入射光的波长无关,只和样品的振动转动 能级有关; b. 在以波数为变量的拉曼光谱图上,斯托克斯线和反斯托克斯线 对称地分布在高强度的瑞利散射线两侧。 c. 一般情况下,斯托克斯线比反斯托克斯线的强度大 激发用单色光波长488nm 纵坐标为谱带强度,横坐标为拉曼位移频率,用波数表示(cm-1 )

6.4拉曼光谱和红外光谱比较verforget how to dream 1.原理比较 拉曼光谱是分子对激发光的散射,而红外光谱则是分子对红外光 的吸收,但两者均是研究分子振动的重要手段,同属分子光谱。 ①红外活性振动一伴有偶极矩变化的振动可以产生红外吸收谱带 1永久偶极矩;极性基团;分子非对称振动 ⅱ瞬间偶极矩;非对称分子; E ②拉曼活性振动一伴随有极化率变化的振动。 诱导偶极矩 p aE 非极性基团,对称分子; 对称振动→拉曼活性;不对称振动→红外活性 拉曼光谱和红外光谱是相互补充的 9
9 6.4 拉曼光谱和红外光谱比较 ①红外活性振动—伴有偶极矩变化的振动可以产生红外吸收谱带 ⅰ永久偶极矩;极性基团;分子非对称振动 ⅱ瞬间偶极矩;非对称分子; ②拉曼活性振动—伴随有极化率变化的振动。 诱导偶极矩 = E 非极性基团,对称分子; 对称振动→拉曼活性;不对称振动→红外活性 E e e r 拉曼光谱是分子对激发光的散射,而红外光谱则是分子对红外光 的吸收,但两者均是研究分子振动的重要手段,同属分子光谱。 拉曼光谱和红外光谱是相互补充的 1. 原理比较

never forget 4拉曼光请和红外光谱批较 how to aream 2.选律比较 振动自由度:3N-5=4 v1S=C-S 拉曼活性 v S-C 红外活性 3 -C-S 红外活性 红外光谱一源于偶极矩变化 拉曼光谱一源于极化率变化 对称中心分子C02,CS2等,选律不相容。 无对称中心分子(例如$0,等),三种振动既是红外活性 振动,又是拉曼活性振动。 10
10 对称中心分子CO2, CS2等,选律不相容。 无对称中心分子(例如SO2等),三种振动既是红外活性 振动,又是拉曼活性振动。 2.选律比较 S C S S C S S C S 1 2 3 4 拉曼活性 红外活性 红外活性 振动自由度:3N- 5 = 4 红外光谱—源于偶极矩变化 拉曼光谱—源于极化率变化 6.4 拉曼光谱和红外光谱比较