
UQSTC 的 956 Modeling and Simulation in Epitaxial Growth
Modeling and Simulation in Epitaxial Growth
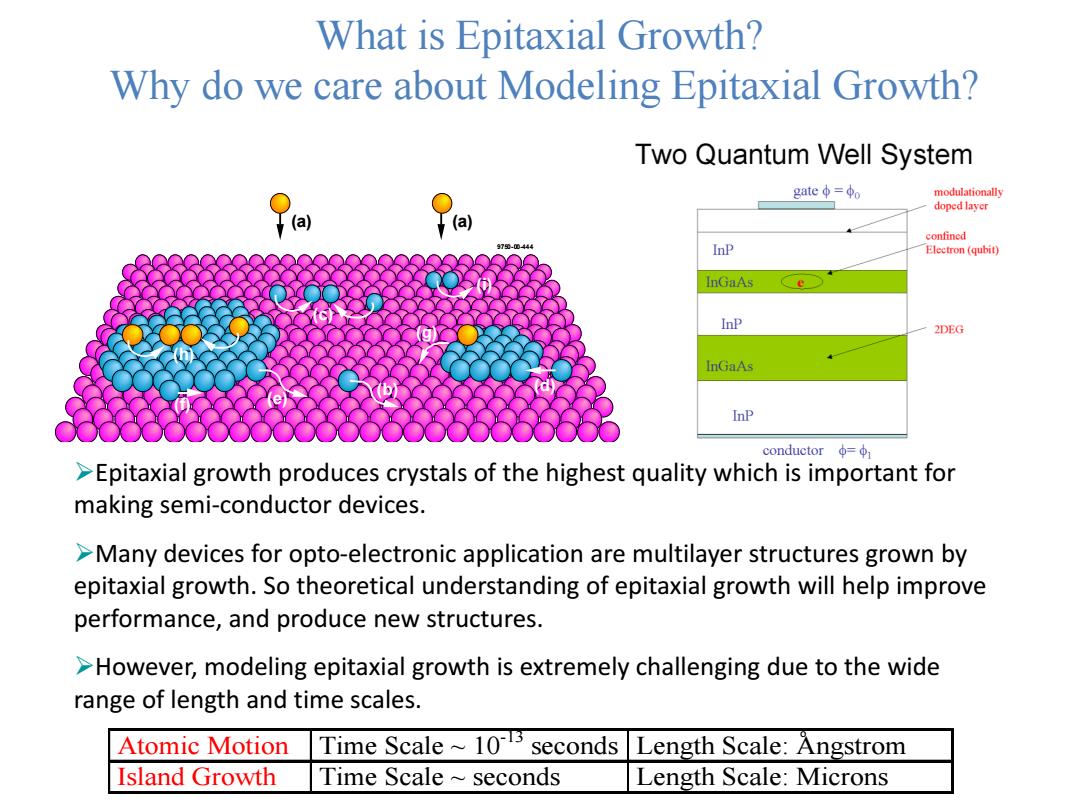
What is Epitaxial Growth? Why do we care about Modeling Epitaxial Growth? Two Quantum Well System gateφ=φo modulationally doped layer (a (a) confined 70-00444 InP Electron(qubit) InGaAs InP 2DEG InGaAs InP conductor=φ1 >Epitaxial growth produces crystals of the highest quality which is important for making semi-conductor devices. >Many devices for opto-electronic application are multilayer structures grown by epitaxial growth.So theoretical understanding of epitaxial growth will help improve performance,and produce new structures. >However,modeling epitaxial growth is extremely challenging due to the wide range of length and time scales. Atomic Motion Time Scale~103 seconds Length Scale:Angstrom Island Growth Time Scale seconds Length Scale:Microns
9750-00-444 (a) (a) (h) (f) (e) (b) (c) (i) (g) (d) What is Epitaxial Growth? Why do we care about Modeling Epitaxial Growth? Atomic Motion Time Scale ~ 10-13 seconds Length Scale: Angstrom Island Growth Time Scale ~ seconds Length Scale: Microns o ➢Epitaxial growth produces crystals of the highest quality which is important for making semi-conductor devices. ➢Many devices for opto-electronic application are multilayer structures grown by epitaxial growth. So theoretical understanding of epitaxial growth will help improve performance, and produce new structures. ➢However, modeling epitaxial growth is extremely challenging due to the wide range of length and time scales

Modeling of Thin Film Growth >Mean-field Rate Equations: Easy to formulate and easy to solve. Contain no spatial information.Do not readily yield information on surface morphology. >Continuum Models:Completely deterministic method. Appropriate mainly at large time and length scales. Lack detail. >KMC simulations:Completely stochastic method. Very useful for identifying relevant microscopic processes. The time and size limitations make them unfeasible for studying epitaxial growth Detailed KMC simulations are extremely slow and expensive
Modeling of Thin Film Growth ➢Mean-field Rate Equations: ✓Easy to formulate and easy to solve. ❖Contain no spatial information. Do not readily yield information on surface morphology. ➢ Continuum Models: Completely deterministic method. ✓Appropriate mainly at large time and length scales. ❖Lack detail. ➢KMC simulations: Completely stochastic method. ✓Very useful for identifying relevant microscopic processes. ❖The time and size limitations make them unfeasible for studying epitaxial growth ❖Detailed KMC simulations are extremely slow and expensive

Smallest Metallic Nanorods Using Physical Vapor Deposition
Smallest Metallic Nanorods Using Physical Vapor Deposition

What are nanorods (wrt thin films) 1μm 1μm US Patent5866204(1999) H.C.Huang,H.L.Wei,C.H.Woo,and By University of Alberta X.X.Zhang,Appl.Phys.Lett.82,4265 (2003)
What are nanorods (wrt thin films) US Patent 5866204 (1999) By University of Alberta H. C. Huang, H. L. Wei, C. H. Woo, and X. X. Zhang, Appl. Phys. Lett. 82, 4265 (2003)
Synthesis methods Atmosphere Multi-Agent Solution Substrate Vacuum Source COMPLEX
Synthesis methods COMPLEX

PVD and GLAD Physical Vapor Deposition Glancing Angle Deposition Substrate Electron Beam Electron Beam Magnetic Field 0 o ao o Magnetic Field H20 H20 H,O H20 Earth Earth Ground Ground 1959 Metallic Nanorods realized from PVD Diffusion distance of metals at room temperature microns Even GLAD should form dense films Nanorod growth is not understood
Physical Vapor Deposition PVD and GLAD Glancing Angle Deposition 1959 Metallic Nanorods realized from PVD Diffusion distance of metals at room temperature = microns Even GLAD should form dense films Nanorod growth is not understood
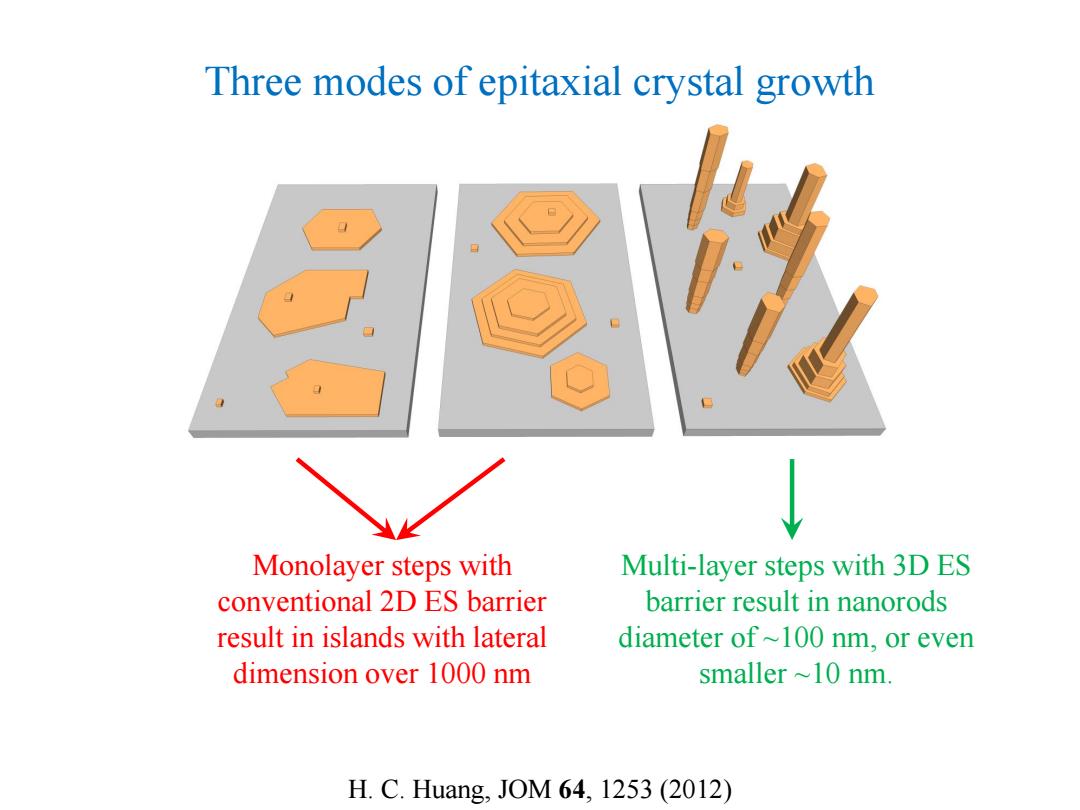
Three modes of epitaxial crystal growth Monolayer steps with Multi-layer steps with 3D ES conventional 2D ES barrier barrier result in nanorods result in islands with lateral diameter of~100 nm,or even dimension over 1000 nm smaller ~10 nm. H.C.Huang,JOM64,1253(2012)
Three modes of epitaxial crystal growth H. C. Huang, JOM 64, 1253 (2012) Monolayer steps with conventional 2D ES barrier result in islands with lateral dimension over 1000 nm Multi-layer steps with 3D ES barrier result in nanorods diameter of ~100 nm, or even smaller ~10 nm
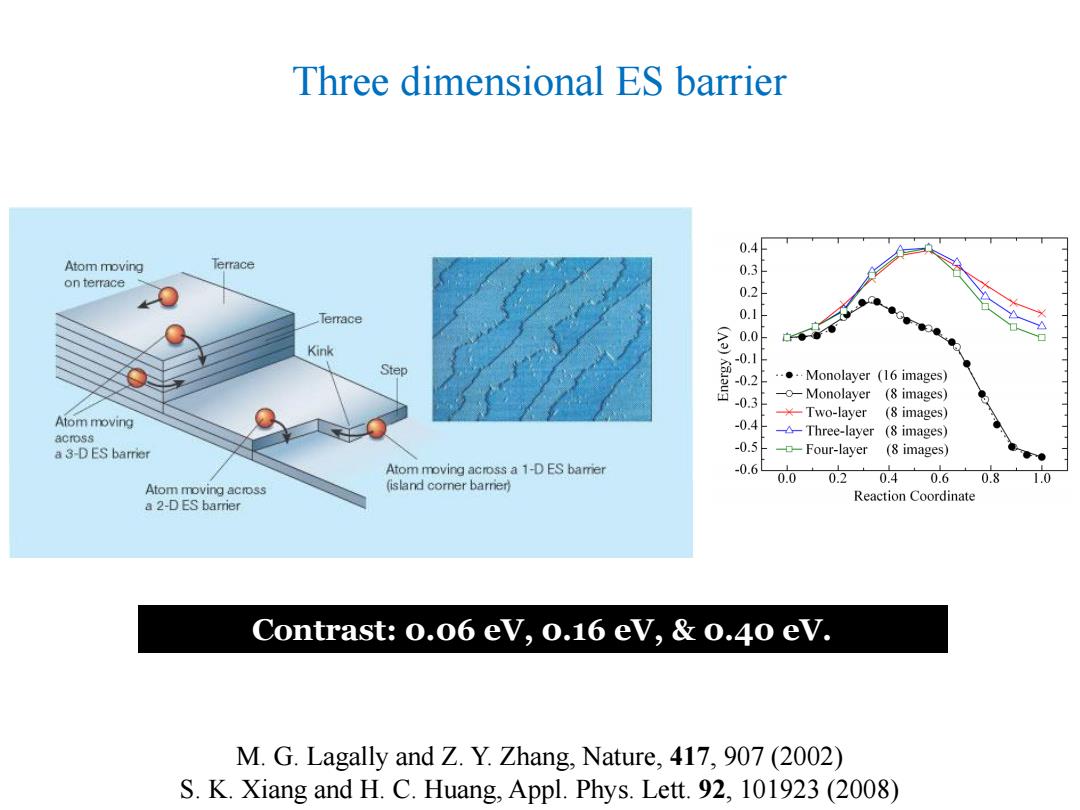
Three dimensional ES barrier Atom moving Terrace on terrace 3a88 Terrace 0.0 白◆ Kink Step 0.1 -0.2 ...Monolayer (16 images) -0.3 -Monolayer (8 images) Atom moving ×-Two-layer (8 images) -0.4 acmoss Three-layer (8 images) a 3-D ES barrier -0.5 -Four-layer (8 images) ● Atom moving across a 1-D ES barer -0.6 Atom moving across (island corner barrer 0.0 0.2 0.4 0.6 0.8 1.0 a 2-D ES barrier Reaction Coordinate Contrast:0.06 ev,0.16 ev,0.40 ev. M.G.Lagally and Z.Y.Zhang,Nature,417,907(2002) S.K.Xiang and H.C.Huang,Appl.Phys.Lett.92,101923(2008)
Contrast: 0.06 eV, 0.16 eV, & 0.40 eV. Three dimensional ES barrier M. G. Lagally and Z. Y. Zhang, Nature, 417, 907 (2002) S. K. Xiang and H. C. Huang, Appl. Phys. Lett. 92, 101923 (2008)
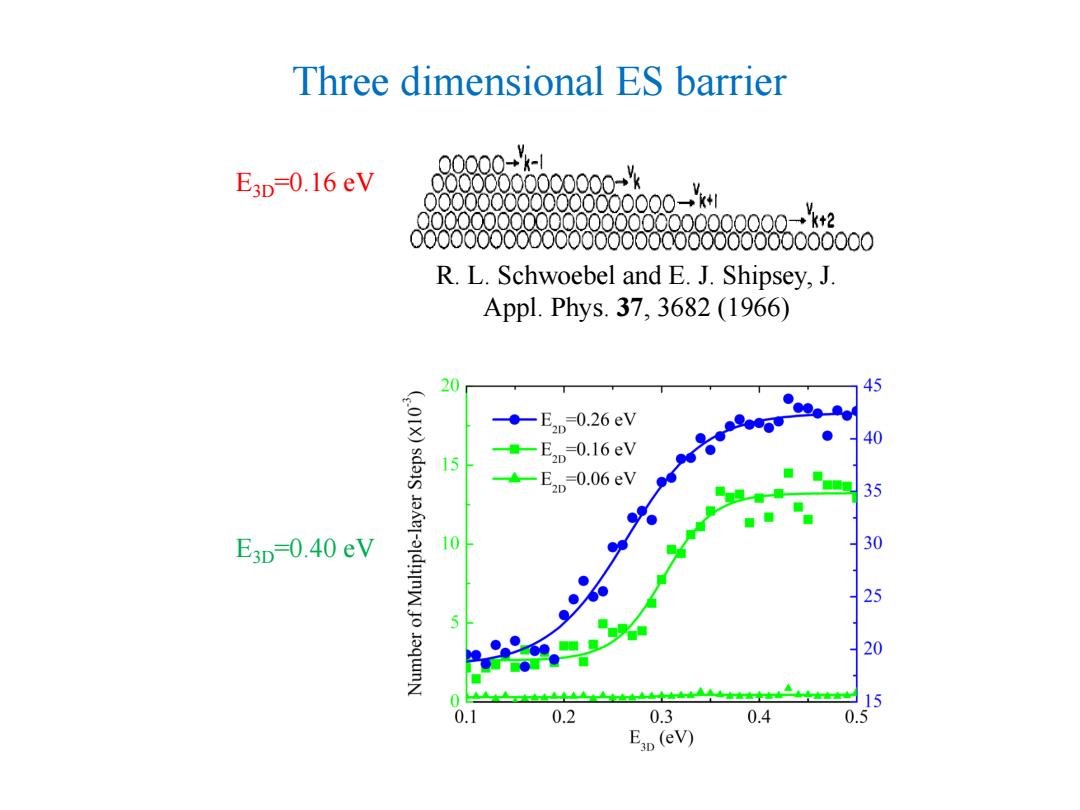
Three dimensional ES barrier E3D-0.16eV 20000000-¥ 000000-¥4 0000000000000000-¥k+2 0000000000000000000000000000000 R.L.Schwoebel and E.J.Shipsey,J. Appl.Phys.37,3682(1966) 20 45 90X ◆E2p-0.26eV das 15 -E2n0.16eV 一 E2-0.06eV 35 E3D-0.40 eV 10 30 25 20 15 0. 0.2 0.3 0.4 0.5 E3(ev)
Three dimensional ES barrier E3D=0.16 eV R. L. Schwoebel and E. J. Shipsey, J. Appl. Phys. 37, 3682 (1966) E3D=0.40 eV