Material Design 12+46 58 tan chrome drive keep Maps G 三 三 3= google now gmail setting hangouts 三 三 3 play games youtube play music clock
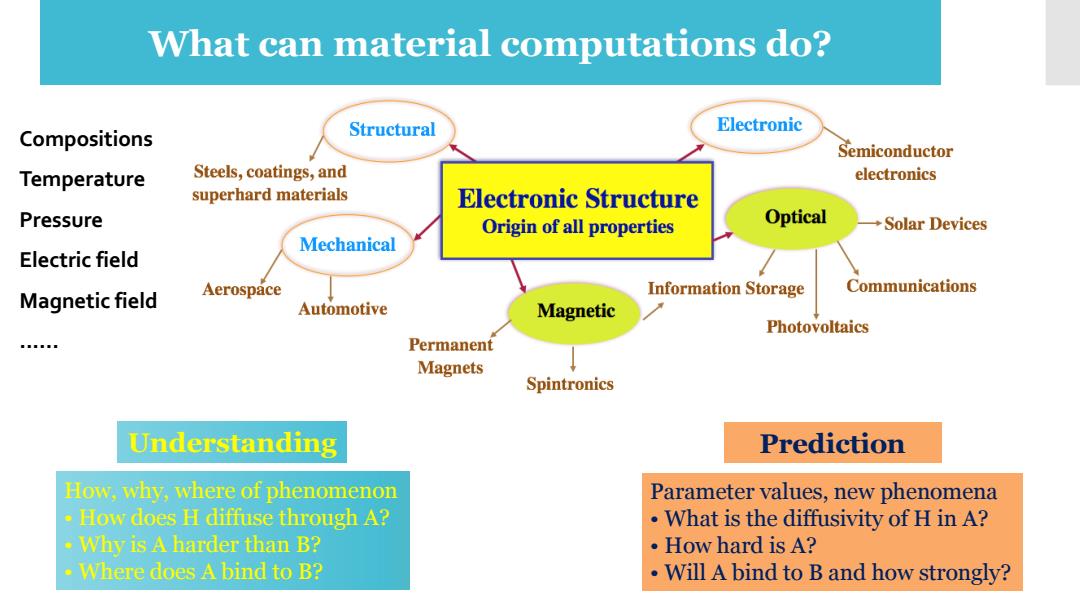
What can material computations do? Structural Electronic Compositions Semiconductor Temperature Steels,coatings,and electronics superhard materials Electronic Structure Pressure Origin of all properties Optical Solar Devices Mechanical Electric field Communications Magnetic field Aerospace Information Storage Automotive Magnetic Photovoltaics Permanent Magnets Spintronics Understanding Prediction How,why,where of phenomenon Parameter values,new phenomena How does H diffuse through A? What is the diffusivity of H in A? Why is A harder than B? How hard is A? ·Where does A bind to B? Will A bind to B and how strongly?
How, why, where of phenomenon • How does H diffuse through A? • Why is A harder than B? • Where does A bind to B? Understanding Prediction Parameter values, new phenomena • What is the diffusivity of H in A? • How hard is A? • Will A bind to B and how strongly? Compositions Temperature Pressure Electric field Magnetic field ...... What can material computations do?
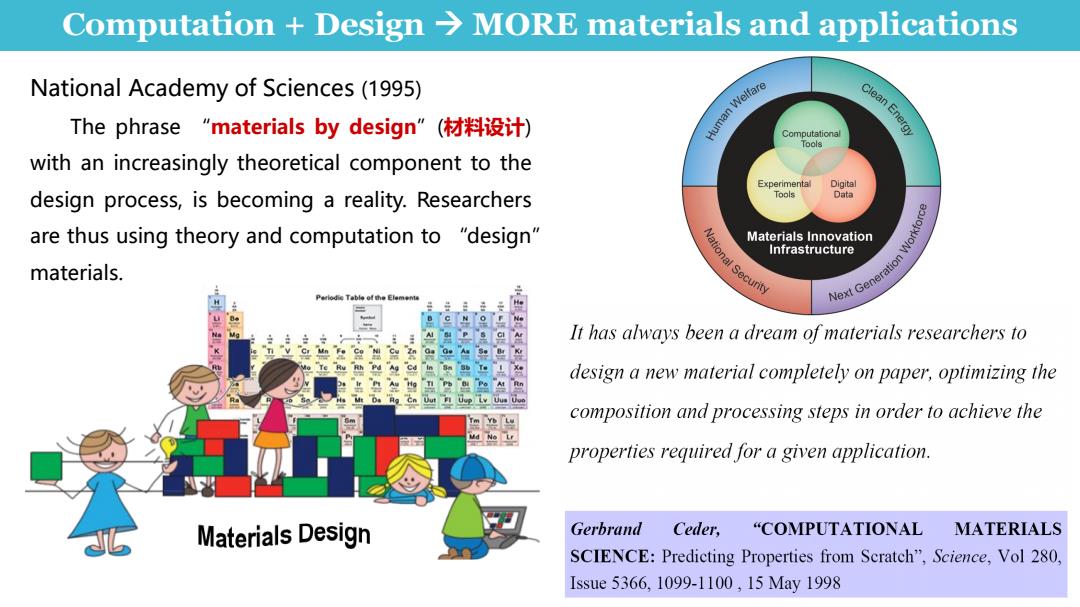
Computation Design>MORE materials and applications National Academy of Sciences(1995) The phrase"materials by design”(材料设计) Human Weifare Clean Energy Computational Tools with an increasingly theoretical component to the Experimental Digital design process,is becoming a reality.Researchers Tools Data are thus using theory and computation to "design" Materials Innovation Workforce Infrastructure materials. It has always been a dream of materials researchers to design a new material completely on paper,optimizing the composition and processing steps in order to achieve the ud No Lr properties required for a given application. Materials Design Gerbrand Ceder,"COMPUTATIONAL MATERIALS SCIENCE:Predicting Properties from Scratch",Science,Vol 280, Issue5366,1099-1100,15May1998
Computation + Design → MORE materials and applications National Academy of Sciences (1995) The phrase “materials by design”(材料设计) with an increasingly theoretical component to the design process, is becoming a reality. Researchers are thus using theory and computation to “design” materials

Editor-in-Chief Alexander M.Korsunsky,PhD MSDE University of Oxford Department of Engineering Science,Parks Road.Oxford, OX1 3PL United Kingdom .com/tand-dcaign Areas of epertise include:fatigue and fracture,dislcations and other defects in solids;residual stresse and eigenstrain theory:surfaces,coatings (nanondentation:(synchrotron)ray methods(diffraction,imaging ELSEVIER Editors materials Geoff Gibson Newcastle University.Newcastle Upon Tyne,United Kingdom ®ESGN Eric Le Bourhis Pprime Institute,Futurescope,France Giang Nguyen EDTOR-IN-CHEF: The University of Adelide.Adelaide.South Australia,Austra Alexander M.Korsunsky Marco Sebastiani Roma Tre University,Roma,Italy Xu Song IChemE吗 The Chinese University of Hong Kong Hong Kong.Hong Kong C8Ss品 Chair Impact Factor: Juan de Pablo,University of Chicago,USA Impact factor: 2018:5.770 2.708* Editorial board members About cover image Claire S Adjiman,Imperial College London,UK dx.doi.org/10.1016/.matdes 2015 0 Linda Broadbelt,Northwestem University,USA Luke Connal,Australian National University,Australia Andrew deMello,ETH ZOrich,Switzerland materialstoday Andrew Ferguson,University of Chicago.USA Kristi Kiick.University of Delaware.USA Yongye Liang.Southern University of Science and Technology.China Patrick Stayton.University of Washington.USA
Impact Factor: 2018: 5.770 Impact factor: 2.708*
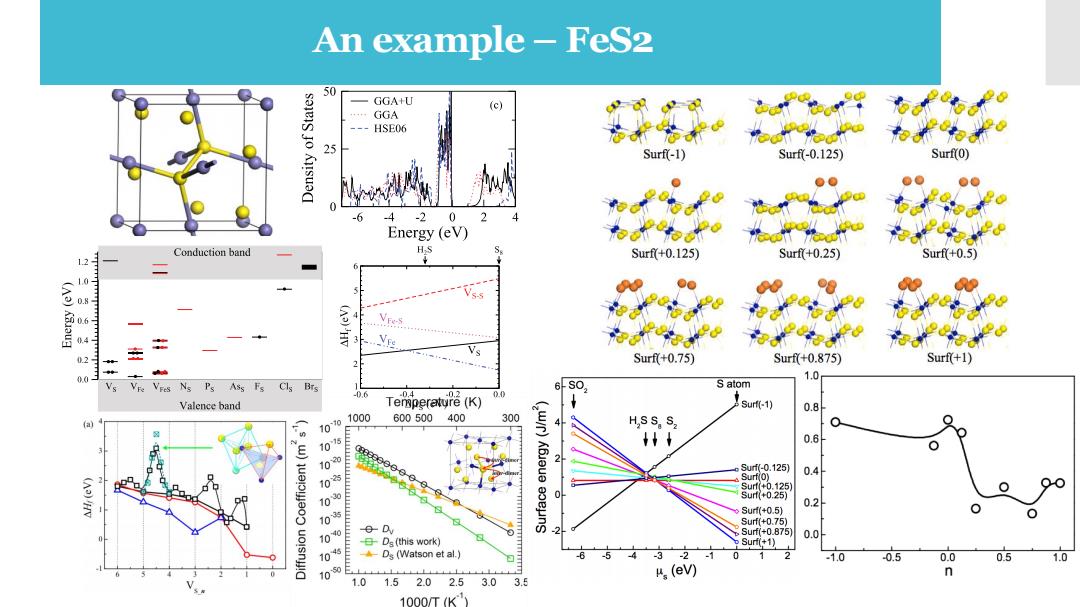
An example-FeS2 50 GGAU (c) GGA HSE06 Surf(-1) Surf-0.125) Surf(0) Ausua -6 .4 -2 0 Energy (eV) Conduction band HS Surf+0.125) Surf+0.25) Surf+0.5】 12 (A)Kaug 4 Vres 1. 3 在 2 Surf+0.75) Surf+0.875) Surf(+1) 0.0 1.0 Vs Ns Ps Ass Fs Cls Brs s0, S atom -0.6 .0.2 Valence band Temperatyre (K) sur(-1) 0.8 1070 1000 600500400 300 ● a H SS,S2 Q t 0.6 020 2 Surf(-0.125) Surf(0) 0.4 0 0 125) 10 0.2 Surf(+0.5) ⊙ Surf+0.75) 100 Surf+0.875) 0.0 日Ds(this work) Surf(+1) 105 ◆Ds(Vatson et al..) 3 2 .1 0 1 -1.0 -0.5 0.0 0.5 1.0 100 n 1.0 1.5 2.02.5 3.0 3.5 (ev) 1000/TK)
An example – FeS2
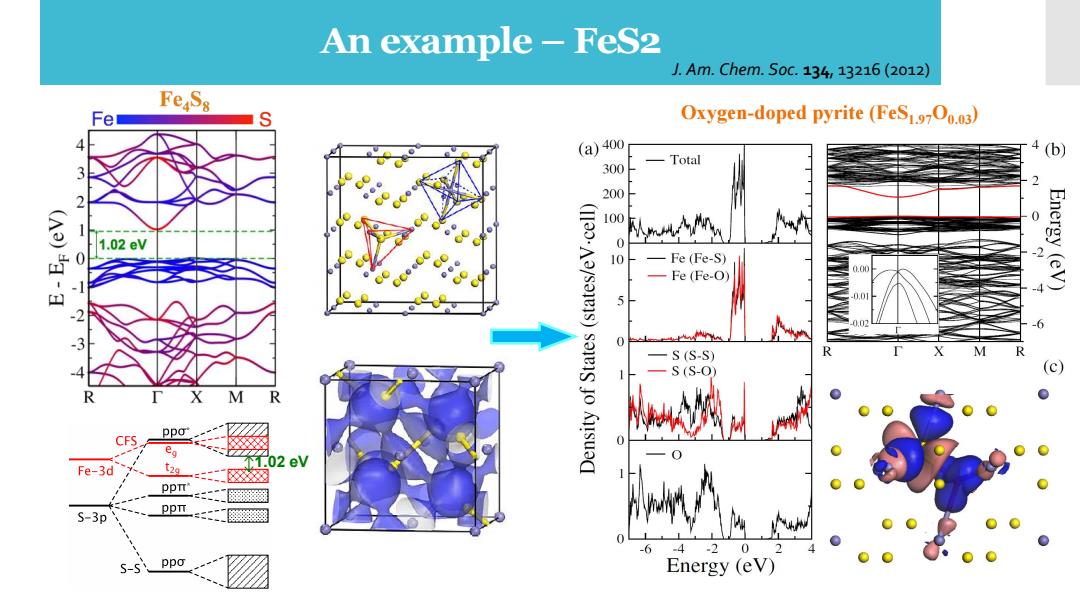
An example-FeS2 J.Am.Chem.S0c.134,13216(2o12) FeS8 Oxygen-doped pyrite(FeS1700.03) (a)400 Total (b) 300 2 200 100 0 (A)- 1.02eV 0 Fe(Fe-S) 2 0.00 Energy(eV) -Fe(Fe-O) 0.0 0.02 S(S-S) R S(S-O) M R CFS ppo ea 1.02 eV Fe-3d PpTT S-3p ppi -2 0 5-s ppo Energy (eV)
1.02 eV An example – FeS2 J. Am. Chem. Soc. 134, 13216 (2012) Oxygen-doped pyrite (FeS1.97O0.03)

An example-FeS2 J.Am.Chem.Soc.134,13216(2012 3 9 10 11 9 10 11 Atomic structures of FeS1.812500.187s alloys in a Atomic structures of FeS1.7500.2s alloys in a 2x2x2 supercell. 2x2×2 supercell
An example – FeS2 Atomic structures of FeS1.8125O0.1875 alloys in a 2×2×2 supercell. J. Am. Chem. Soc. 134, 13216 (2012) Atomic structures of FeS1.75O0.25 alloys in a 2×2×2 supercell
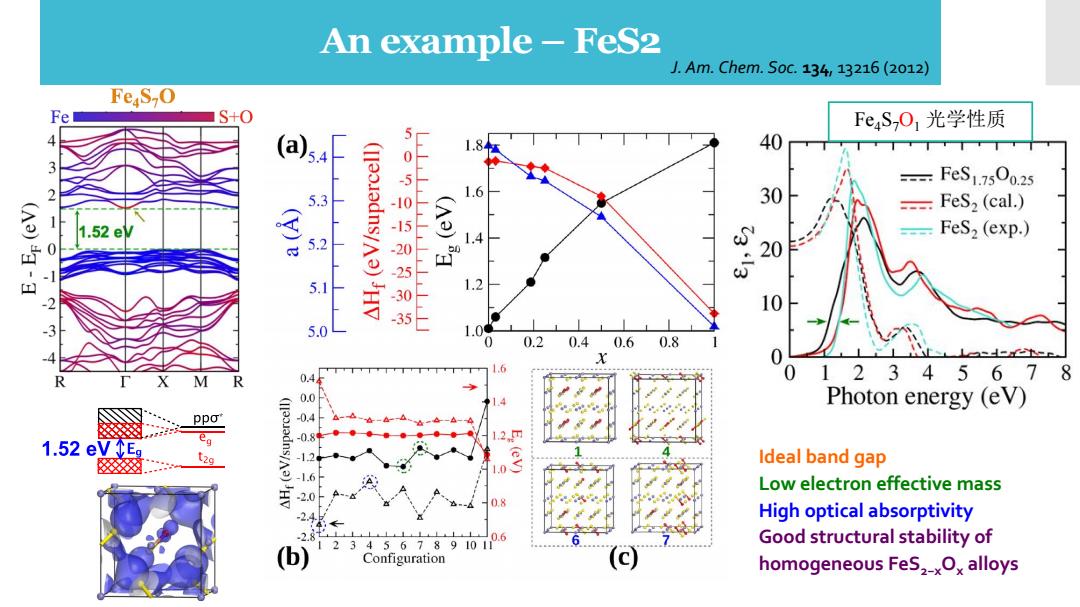
An example-FeS2 J.Am.Chem.S0c.134,13216(2012) FeS-O Fe S+0 FeSO1光学性质 (a54 40 3 (II35.adns/A3)JHV 50500520505 FeS1.750o.25 5.3 6 30 -FeS2 (cal.) 1.52e -FeS2 (exp.) 5.2 20 5.1 1.2 10 5.0 1.0 0.20.40.60.8 0 1.6 0.4 01234567 8 Photon energy (eV) ppo 1.2 1.52 eVEg t2a -12 E.(ev) Ideal band gap 1.6 04 Low electron effective mass High optical absorptivity 28 0.6 3456789101 Good structural stability of (b) Configuration homogeneous FeS2-xOx alloys
Fe4S7O1 光学性质 Ideal band gap Low electron effective mass High optical absorptivity Good structural stability of homogeneous FeS2−xOx alloys An example – FeS2 J. Am. Chem. Soc. 134, 13216 (2012)
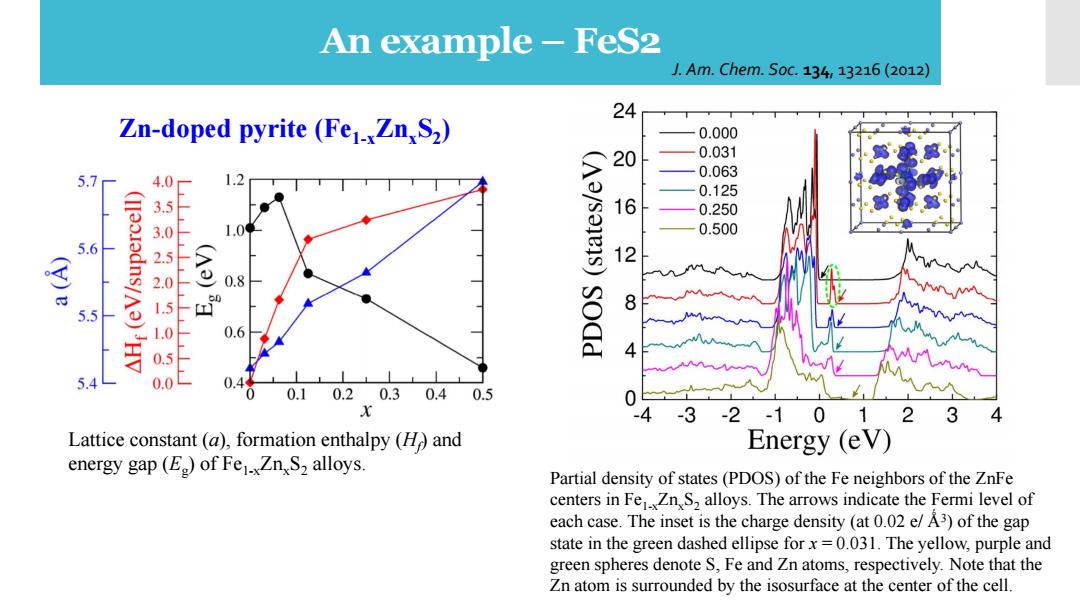
An example-FeS2 J.Am.Chem.S0c.134,13216(2012) 24 Zn-doped pyrite (Fe1xZn,S2) 0.000 0.031 5.7 4.0 20 0.063 0.125 1 0.250 0.500 5.6 12 0.8 8 5.5 500150150 0.6 sodd 0.0 0.44 0.10.20.3 0.40.5 x 3 -2-10 12 3 4 Lattice constant (a),formation enthalpy (H and Energy (eV) energy gap(E)of Fe1.Zn S2 alloys. Partial density of states(PDOS)of the Fe neighbors of the ZnFe centers in FeZnS2 alloys.The arrows indicate the Fermi level of each case.The inset is the charge density (at 0.02 e/A3)of the gap state in the green dashed ellipse forx=0.031.The yellow,purple and green spheres denote S,Fe and Zn atoms,respectively.Note that the Zn atom is surrounded by the isosurface at the center of the cell
An example – FeS2 Partial density of states (PDOS) of the Fe neighbors of the ZnFe centers in Fe1-xZnxS2 alloys. The arrows indicate the Fermi level of each case. The inset is the charge density (at 0.02 e/ Ǻ3 ) of the gap state in the green dashed ellipse for x = 0.031. The yellow, purple and green spheres denote S, Fe and Zn atoms, respectively. Note that the Zn atom is surrounded by the isosurface at the center of the cell. J. Am. Chem. Soc. 134, 13216 (2012) Lattice constant (a), formation enthalpy (Hf ) and energy gap (Eg ) of Fe1-xZnxS2 alloys. Zn-doped pyrite (Fe1-xZnxS2 )
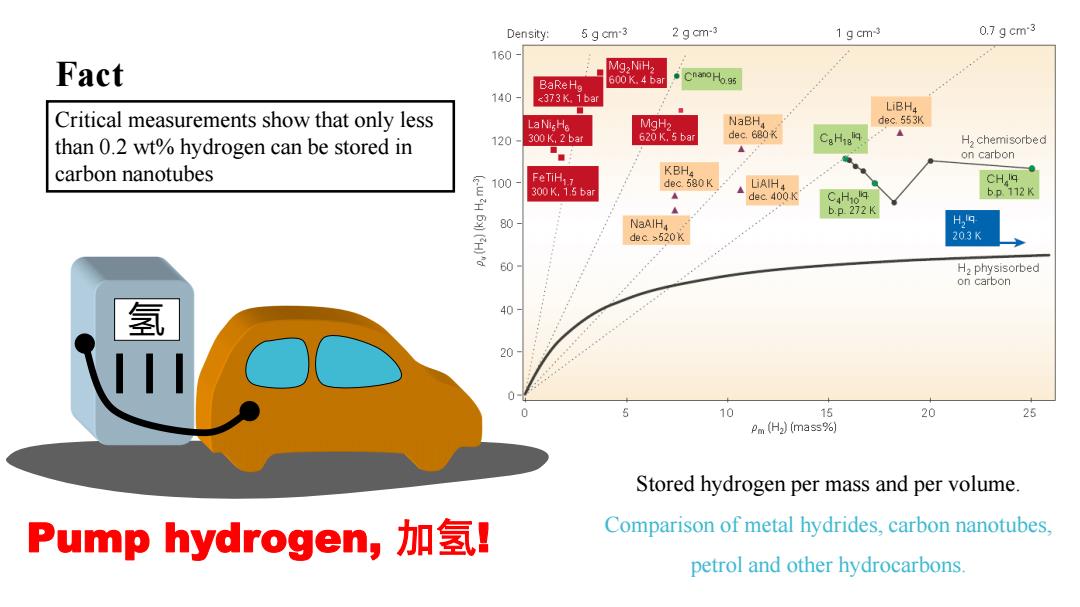
Density: 5 g cm-3 2 g cm-3 1 gcm3 0.7gcm-3 160 Fact Mg,NiH, BaRe Ho 600 K.4 bar Cnano Ho.95 140 520K 203K 60 H,physisorbed on carbon 氢 % 20 5 10 15 20 25 Pm (H2)(mass%) Stored hydrogen per mass and per volume. Pump hydrogen,加氢l Comparison of metal hydrides,carbon nanotubes, petrol and other hydrocarbons
Stored hydrogen per mass and per volume. Comparison of metal hydrides, carbon nanotubes, petrol and other hydrocarbons. 氢 Pump hydrogen, 加氢! Fact Critical measurements show that only less than 0.2 wt% hydrogen can be stored in carbon nanotubes