
3D-Bulk systems Periodic in three dimensions ·Crystal structures Defects and impurities ·Elastic modulus Electronic/orbital properties ·Magnetic properties
Crystal structures Defects and impurities Elastic modulus Electronic/orbital properties Magnetic properties 3D – Bulk systems Periodic in three dimensions
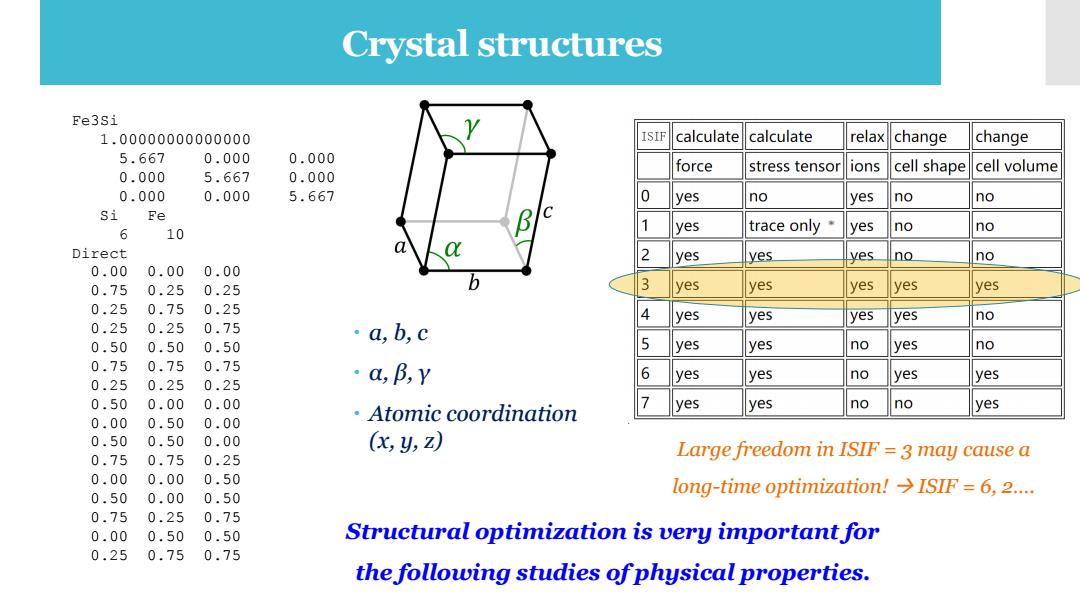
Crystal structures Fe3si 1 1.00000000000000 ISIF calculate calculate relax change change 5.667 0.000 0.000 force stress tensor ions cell shape cell volume 0.000 5.667 0.000 0.000 0.000 5.667 0 yes no yes no no Si Fe o 10 1 yes trace only" yes no no Direct 2 yes yes yes no no 0.00 0.00 0.00 0.75 0.25 0.25 3 yes yes yes yes yes 0.25 0.75 0.25 4 yes yes yes yes no 0.25 0.25 0.75 ·a,b,c 0.50 0.500.50 5 yes yes no yes no 0.75 0.750.75 ·a,B,Y 6 yes yes no yes yes 0.25 0.250.25 0.50 0.000.00 yes yes no no yes 0.00 0.500.00 ·Atomic coordination 0.50 0.500.00 (,y,z) 0.75 0.75 0.25 Large freedom in ISIF 3 may cause a 0.00 0.000.50 0.50 0.00 0.50 long-time optimization!>ISIF 6,2.... 0.75 0.25 0.75 0.00 0.500.50 Structural optimization is very important for 0.25 0.75 0.75 the following studies ofphysical properties
Crystal structures a, b, c α, β, γ Atomic coordination (x, y, z) Fe3Si 1.00000000000000 5.667 0.000 0.000 0.000 5.667 0.000 0.000 0.000 5.667 Si Fe 6 10 Direct 0.00 0.00 0.00 0.75 0.25 0.25 0.25 0.75 0.25 0.25 0.25 0.75 0.50 0.50 0.50 0.75 0.75 0.75 0.25 0.25 0.25 0.50 0.00 0.00 0.00 0.50 0.00 0.50 0.50 0.00 0.75 0.75 0.25 0.00 0.00 0.50 0.50 0.00 0.50 0.75 0.25 0.75 0.00 0.50 0.50 0.25 0.75 0.75 Large freedom in ISIF = 3 may cause a long-time optimization! → ISIF = 6, 2…. Structural optimization is very important for the following studies of physical properties
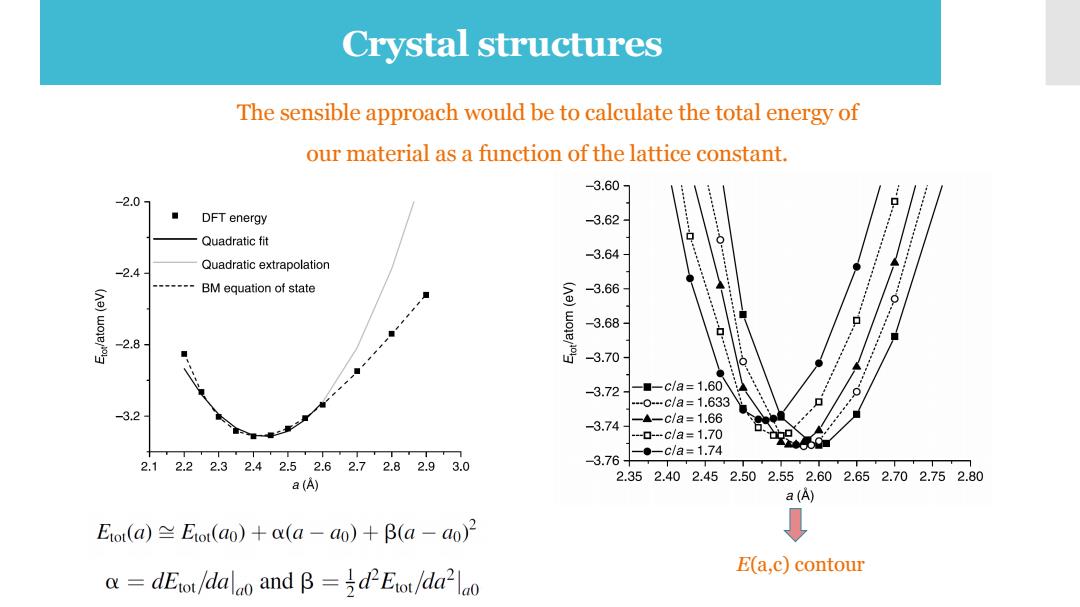
Crystal structures The sensible approach would be to calculate the total energy of our material as a function of the lattice constant. -3.60 2.0 DFT energy -3.62 Quadratic fit -3.64 Quadratic extrapolation -2.4- BM equation of state 金 -3.66 -3.68 -2.8 ◆ -3.70 ◆ -3.72 ■-c/a=1.60 -0-…c/a=1.633 -3.2 -3.74 -▲-c/a=1.66 -0-…c/a=1.70 2.12.22.32.42.52.62.72.82.93.0 -3.76+ -●-c/a=1.74 a(A) 2.352.40 2.452.502.552.602.652.702.752.80 a(A) Etou(a)Eou(ao)+a(a-ao)+B(a-ao)2 E(a,c)contour =dEror/dalao and B=dEtr/da2lo
Crystal structures The sensible approach would be to calculate the total energy of our material as a function of the lattice constant. E(a,c) contour

Crystal structures VASP Phonopy supercell>phonon dispersion https://atztogo.github.io/phonopy/ In physics,a phonon is a collective excitation in a 16 periodic,elastic arrangement of atoms or molecules in 14 condensed matter.It represents an excited state in the 12 quantum mechanical quantization of the modes of 10 vibrations of elastic structures of interacting particles. The phonon dispersion curves are calculated along 6 several lines of high symmetry,and only the phonon frequency density of states are required rather the dispersion curves. WKrL UW L K
Crystal structures VASP + Phonopy + supercell → phonon dispersion The phonon dispersion curves are calculated along several lines of high symmetry, and only the phonon frequency density of states are required rather the dispersion curves. In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter. It represents an excited state in the quantum mechanical quantization of the modes of vibrations of elastic structures of interacting particles. https://atztogo.github.io/phonopy/
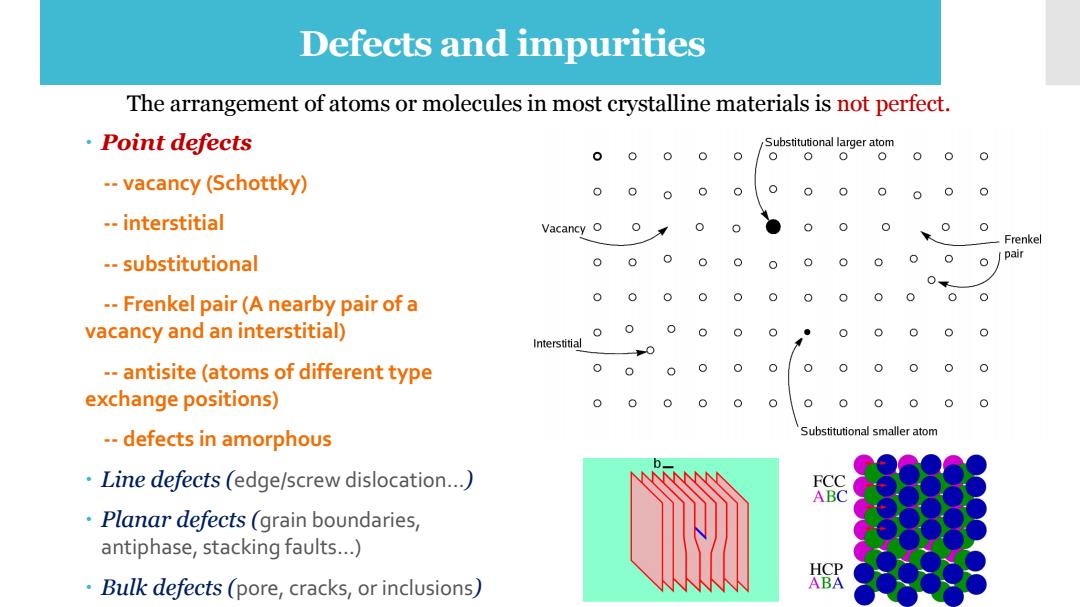
Defects and impurities The arrangement of atoms or molecules in most crystalline materials is not perfect. ·Point defects Substitutional larger atom 0000 0 --vacancy (Schottky) 0 0 0 --interstitial Vacancy O 0 0 Frenkel --substitutional 000 ● 0 0 O --Frenkel pair(A nearby pair of a 00 0 vacancy and an interstitial) Interstitial --antisite(atoms of different type 0 0 exchange positions) 0 --defects in amorphous Substitutional smaller atom Line defects (edge/screw dislocation...) Planar defects(grain boundaries, antiphase,stacking faults...) HCP Bulk defects(pore,cracks,or inclusions) ABA
Defects and impurities Point defects -- vacancy (Schottky) -- interstitial -- substitutional -- Frenkel pair (A nearby pair of a vacancy and an interstitial) -- antisite (atoms of different type exchange positions) -- defects in amorphous Line defects (edge/screw dislocation…) Planar defects (grain boundaries, antiphase, stacking faults…) Bulk defects (pore, cracks, or inclusions) The arrangement of atoms or molecules in most crystalline materials is not perfect
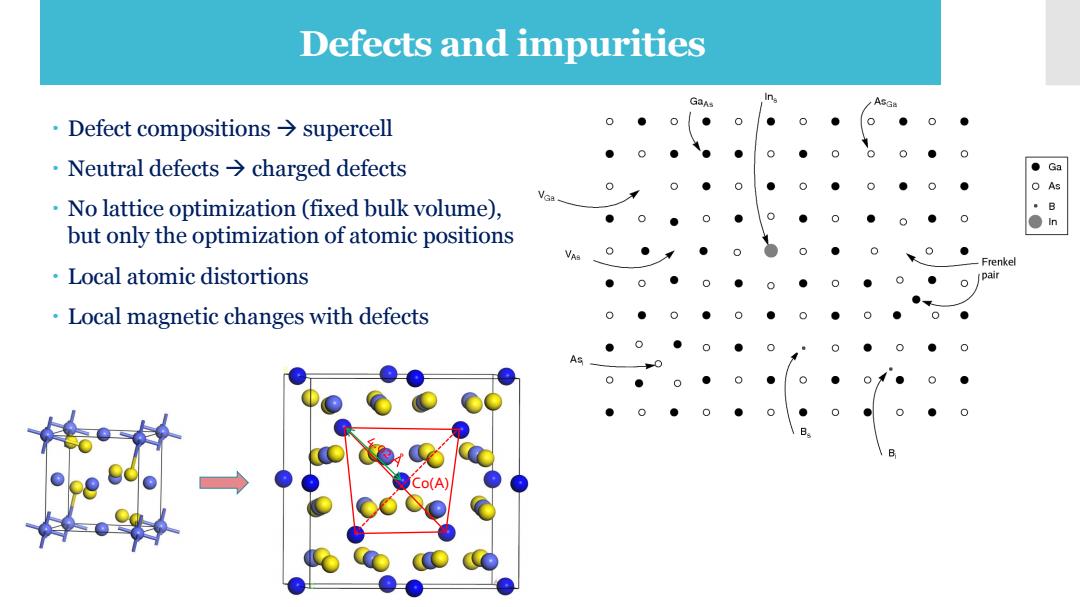
Defects and impurities GaAs ASGa ·Defect compositions→supercell 0●0 ● ● ● ●0 ·Neutral defects→charged defects ●Ga As No lattice optimization (fixed bulk volume), ●0 ● ●n but only the optimization of atomic positions ●) Frenkel Local atomic distortions (pair Local magnetic changes with defects 0
Defects and impurities Co(A) Defect compositions → supercell Neutral defects → charged defects No lattice optimization (fixed bulk volume), but only the optimization of atomic positions Local atomic distortions Local magnetic changes with defects
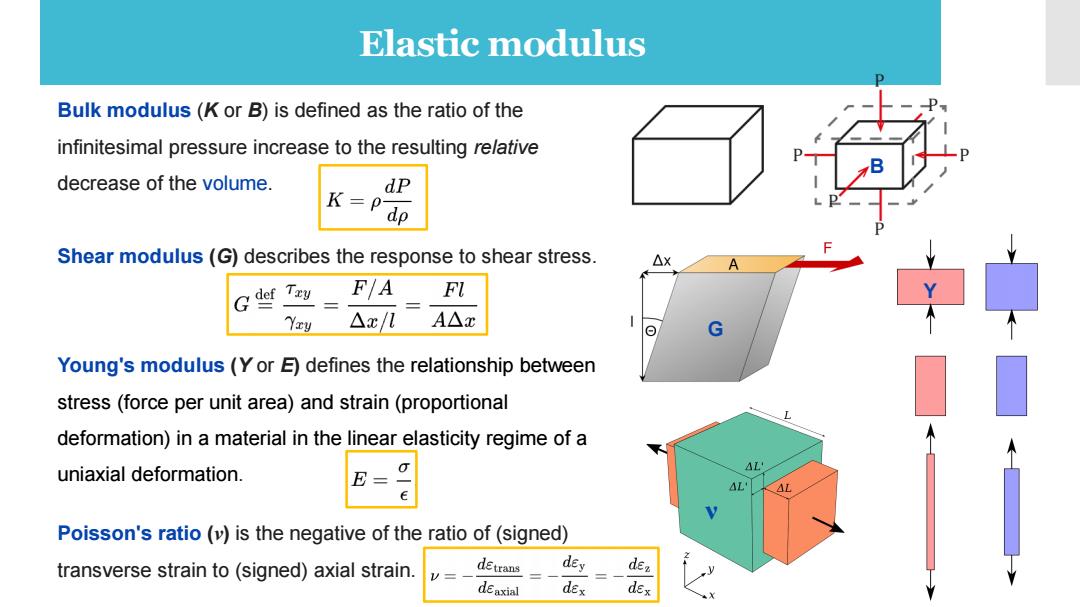
Elastic modulus Bulk modulus(K or B)is defined as the ratio of the infinitesimal pressure increase to the resulting relative decrease of the volume. dP K=P dp Shear modulus(G)describes the response to shear stress. △X G def Tzy FA Fl Yay △x/U A△x Young's modulus (Y or E)defines the relationship between stress(force per unit area)and strain(proportional deformation)in a material in the linear elasticity regime of a uniaxial deformation. AL' AL Poisson's ratio(v)is the negative of the ratio of(signed) transverse strain to(signed)axial strain. V= detrans dey dez deaxial dex dex
Elastic modulus Bulk modulus (K or B) is defined as the ratio of the infinitesimal pressure increase to the resulting relative decrease of the volume. Shear modulus (G) describes the response to shear stress. Young's modulus (Y or E) defines the relationship between stress (force per unit area) and strain (proportional deformation) in a material in the linear elasticity regime of a uniaxial deformation. Poisson's ratio (ν) is the negative of the ratio of (signed) transverse strain to (signed) axial strain. B G ν Y

K- E= 入= G- V= M= (K,E) 3K(3K-E) 3KE 3K-E 3K(3K+E) 9K-E 9K-E 6K 9K-E (K,) 9K(K-X) 3(K-) 3K-2λ 3K- 2 3K- (K,G) 9KG 3K-2G 3K+G K-9 23K+G) K+9 (K,) 3K(1-2w) 3Kv 3K1-2w) 3K(1-) Bulk modulus(灯 1+0 21+) 1+形 (K,M) 9K(M-K) 3K-M 3(M-K) 3K-M Shear modulus(G) 3K+M 4 3K+M (E,) E+3A+R E-3A+R 2A E-A+R Young's modulus (E) 6 4 EHA+R 2 (E,G) EG G(E-2G) G(4G-E) 3(3G-E 易-1 Poisson's ratio (v) 3G-E 3G-E E Ev (E,w) E E(1-w) 3(1-2) (1+w)(1-2) 21+) Lame's first parameter (4) (1+w1-2) P-wave modulus (M) (E,M) 3M-E+S M-E+S 3M+E-S E-M+S 6 4 8 4M Homogeneous isotropic linear elastic materials have their (入,G) A+婴 G3入+2G) 入 入+2G λ+G 2(A+G) elastic properties uniquely (A,) (1+ A(1+w)1-2w) A1-2)) A(1- 3 2v determined by any two moduli (A,M) M+2X (M-A(M+2A) M-X 3 M+λ 2 among these;thus,given any (G,) 2G1+w) 31-2) 2G1+w) 2Gv 2G1-) 1-2 two,any other of the elastic 1-2w (G,M) M-9 G(3M-4G) M-2G M-2G moduli can be calculated M-G 2M-2G (w,M) M1+) M(1+01-2) Mv M(1-2) according to these formulas. 3(1-) 1- 1-2 2(1-)
Elastic modulus Homogeneous isotropic linear elastic materials have their elastic properties uniquely determined by any two moduli among these; thus, given any two, any other of the elastic moduli can be calculated according to these formulas. Bulk modulus (K) Shear modulus (G) Young's modulus (E) Poisson's ratio (ν) Lamé's first parameter (λ) P-wave modulus (M)

INSTTTUTE OF PHYSICS PUBLISHENG Elastic modulus J.Phys.:Condens.Matter 15 (2003)5307-5314 PLS953-898403162293-9 The elastic energy of a solid under strain is given by Ab initio elastic constants for the lonsdaleite phases of C,Si and Ge V 6 6 △E= SQ Wang and H Q Ye! Cijeiej GPa GPa Nb A-0.5 Fe A-2.4 150 V is the volume of the undistorted lattice cell,E is the energy 140 130 increment from the strain with vector e=(e,e2,e3,e,es,e6) 100 20 0 200 C is the matrix of the elastic constants. 100 100 100 0 100 100 160 For cubic phases--three independent elastic constants,Cu,C2 and C4; -100 0 0 100 -100 000 -100 100 140 For hexagonal phases--two more independent elastic constants,C13 and C33. The primitive vectors of a cubic diamond structure are defined as 一2 245 .(I+e) 0 22 学 22
Elastic modulus The elastic energy of a solid under strain is given by V is the volume of the undistorted lattice cell, E is the energy increment from the strain with vector e = (e1 , e2 , e3 , e4 , e5 , e6 ). C is the matrix of the elastic constants. For cubic phases -- three independent elastic constants, C11, C12 and C44; For hexagonal phases -- two more independent elastic constants, C13 and C33. The primitive vectors of a cubic diamond structure are defined as

△X A Elastic modulus For the cubic phase, For the hexagonal phase, apply the tri-axial shear strain e △E 3 △E C462 e=(0,0,0,8,8,0) (0,0,0,6,6,6)to getC44 =C4462 2 apply the volume-conserving △E e=(6,8,0,0,0,0) (C1+C12)82 = orthorhombic strain e=(δ, △E =6C82+0(83) 8,(1+8)-2-1,0,0,0)to △E e=(0,0,0,0,0,8) =4(C1-C12)82 getC'=(C11-C12)/2 △E apply the strain under hydrostatic △E 9 e=(0,0,8,0,0,0) pressure e=(8,6,8,o,o,o)to B82 2 get B △E 9 e=(⑥,8,8,0,0,0) B82 3B+4C C1= 3 B=2/9(C1+C12+2C13+C33/2) 3B-2C C12二 3
Elastic modulus G apply the tri-axial shear strain e = (0, 0, 0, δ, δ, δ) to get C44 For the cubic phase, apply the volume-conserving orthorhombic strain e = (δ, δ, (1 + δ)−2−1, 0, 0, 0) to get C’ = (C11-C12)/2 apply the strain under hydrostatic pressure e = (δ, δ, δ, 0, 0, 0) to get B For the hexagonal phase, e = (δ, δ, 0, 0, 0, 0) e = (0, 0, 0, 0, 0, δ) e = (0, 0, δ, 0, 0, 0) e = (0, 0, 0, δ, δ, 0) e = (δ, δ, δ, 0, 0, 0) B = 2/9(C11 + C12 + 2C13 + C33/2)